【数学】甘肃省武威市第十八中学2019-2020学年高一上学期期末考试试题（解析版） 10页

甘肃省武威市第十八中学2019-2020学年高一上学期 期末考试数学试题 一、选择题（每小题5分，共12小题）‎ ‎1.已知点，，则直线的斜率是（ ）‎ A. B. C. 5 D. 1‎ ‎【答案】D ‎【解析】由题意，根据直线的斜率公式，可得直线的斜率，故选D.‎ ‎2.下列函数中，既是奇函数又在定义域上是增函数为（ ）．‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 选项，在定义域上是增函数，但是是非奇非偶函数，故错；‎ 选项，是偶函数，且在上是增函数，在上是减函数，故错；‎ 选项，是奇函数且在和上单调递减，故错；‎ 选项，是奇函数，且在上是增函数，故正确．‎ 综上所述，故选．‎ ‎3.用斜二测画法画一个水平放置的平面图形的直观图是如图所示的一个正方形，则原来的图形是（ ）．‎ A. B. ‎ C. D. 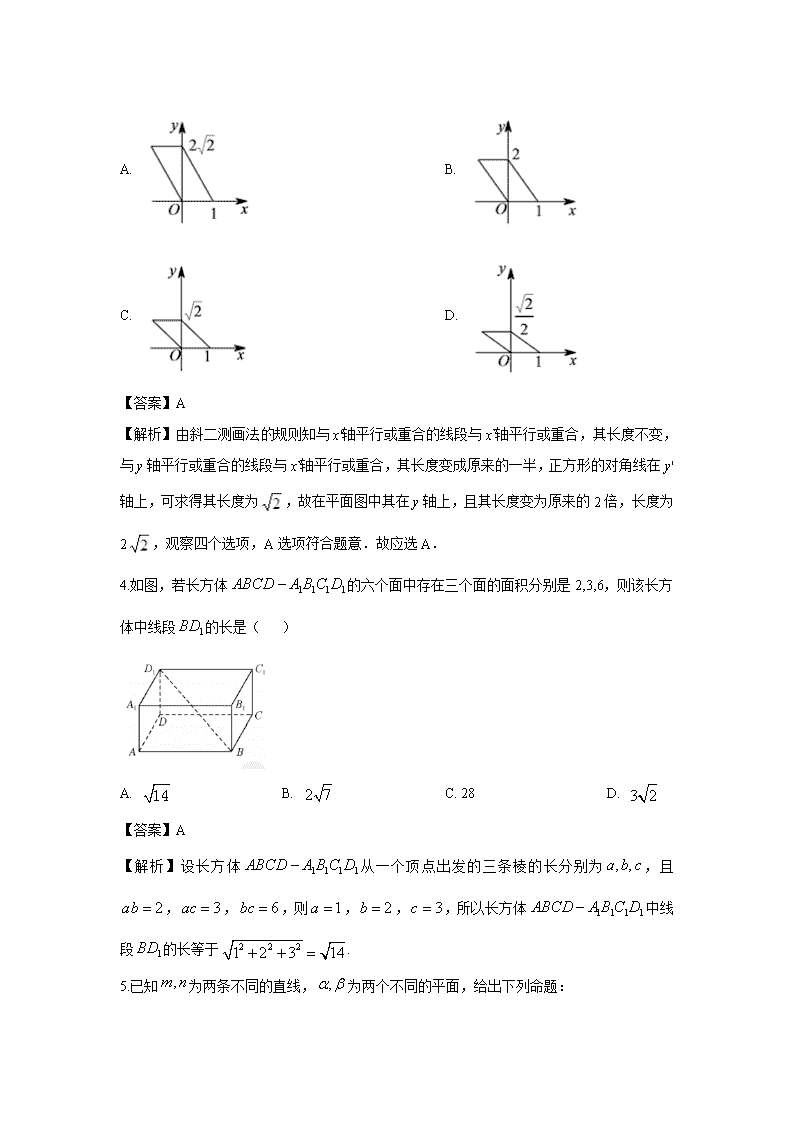‎ ‎【答案】A ‎【解析】由斜二测画法规则知与x'轴平行或重合的线段与x’轴平行或重合，其长度不变，与y轴平行或重合的线段与x’轴平行或重合，其长度变成原来的一半，正方形的对角线在y'轴上，可求得其长度为，故在平面图中其在y轴上，且其长度变为原来的2倍，长度为2，观察四个选项，A选项符合题意．故应选A．‎ ‎4.如图，若长方体的六个面中存在三个面的面积分别是2,3,6，则该长方体中线段的长是（ ）‎ A. B. C. 28 D. ‎ ‎【答案】A ‎【解析】设长方体从一个顶点出发的三条棱的长分别为，且，，，则，，，所以长方体中线段的长等于.‎ ‎5.已知为两条不同的直线，为两个不同的平面，给出下列命题：‎ ‎①若，，则；②若，，则；③若，，则；④若，，，则.其中正确的命题是（ ）‎ A. ②③ B. ①③ C. ②④ D. ①④‎ ‎【答案】B ‎【解析】垂直于同一条直线的两个平面互相平行,故①对；平行于同一条直线的两个平面相交或平行，故②错；若，，，则或与为异面直线或与为相交直线，故④错；若，则存在过直线的平面，平面交平面于直线，，又因为，所以，又因为平面，所以，故③对.‎ 故选B.‎ ‎6.函数的定义域是( )‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】函数的定义域需满足 解得 且 ‎ 故选D ‎7.已知，，，则的大小关系是( )‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】由题意可得，‎ 所以，选B.‎ ‎8.函数y＝在[2，3]上的最小值为(　　)‎ A. 2 B. ‎ C. D. －‎ ‎【答案】B ‎【解析】y＝在[2，3]上单调递减，所以x=3时取最小值为，选B.‎ ‎9.已知正方体外接球的体积是，则此正方体的棱长是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】设正方体的棱长为，则体对角线长为，即外接球的直径为，故由，得.‎ ‎10.函数的零点所在的区间（ ）‎ A. B. C. （1,2） D. （2,3）‎ ‎【答案】C ‎【解析】由于，‎ 根据零点存在性定理可知，函数的零点在区间.‎ 故选:C.‎ ‎11.的图象为　　‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】由可知函数的定义域为：或，函数的图象关于对称，‎ 由函数的图象，可知，A、B、D不满足题意．‎ 故选C．‎ ‎12.设函数是奇函数，在内是增函数，又，则的 解集是（ ）．‎ A B. ‎ C. D. ‎ ‎【答案】D ‎【解析】函数是奇函数，在内是增函数，又，‎ ‎，且在内是增函数，‎ ‎，‎ ‎①当时，‎ ‎②当时，‎ ‎③当时，不等式的解集为 综上，的解集为 故选 二、填空题（每小题5分，共4小题）‎ ‎13.若函数为偶函数，则_______‎ ‎【答案】1‎ ‎【解析】函数 函数为偶函数，‎ ‎14.某几何体的三视图如图所示，该几何体的体积是________．‎ ‎【答案】56‎ ‎【解析】依题意，可得几何体的直观图如下所示 几何体四棱柱，故体积 故答案为：‎ ‎15.若将边长为的正方形绕着它的一边所在的直线旋转一周，则所得圆柱的侧面积为________.‎ ‎【答案】‎ ‎【解析】将边长为的正方形绕着它的一边所在的直线旋转一周，‎ 所得圆柱的高与底面半径都是2，‎ 所以其侧面积为，故答案为.‎ ‎16.在直三棱柱中,若 ，则异面直线与所成的角等于_________‎ ‎【答案】‎ ‎【解析】三棱柱为直三棱柱,且 ‎ 以点 为坐标原点，分别以，，为 轴建立空间直角坐标系 设，则 ‎ , ,,‎ ‎，‎ 又 异面直线所成的角在 ‎ ‎ 异面直线与所成的角等于 ．‎ 三、解答题（每小题10分，共4小题）‎ ‎17.已知直线经过点，，直线经过点，.‎ ‎（1）若∥求a的值；‎ ‎（2）若，求a的值.‎ 解：（1）直线经过点，，‎ 的斜率为；‎ 直线经过点，，的斜率为，‎ 若，则，解得或；‎ ‎（2）若，当时，此时，，与题干不符；‎ 当时，的斜率存在，则，‎ 解得或．‎ 故当或时两直线垂直.‎ ‎18.如图，在三棱柱中，、分别是棱、的中点，求证：平面平面．‎ 解：证明：设与的交点为，连结，‎ 四边形为平行四边形，为中点，‎ 又是的中点，是三角形的中位线，则，‎ 又平面，平面，‎ 平面；‎ 为线段的中点，点是的中点，‎ 且，则四边形为平行四边形，‎ ‎，‎ 又平面，平面，‎ 平面．‎ 又平面，，且平面，平面，‎ 平面平面．‎ ‎19.如图，已知四棱锥，底面四边形为菱形，，．分别是线段．的中点．‎ ‎（1）求证：∥平面；‎ ‎（2）求异面直线与所成角的大小．‎ 解：（1）解：连接交于点，∵分别是线段的中点,‎ ‎∴．‎ ‎∵平面，平面 ‎∴平面．‎ ‎（2）解：由（1）知，就是异面直线 与所成的角或其补角．‎ ‎∵四边形为菱形，，，‎ ‎∴在△中，，，∴，‎ ‎∴异面直线与所成的角为．‎ ‎20.如图，在三棱锥中，D为线段的中点，E为线段上一点.‎ ‎（1）求证：；‎ ‎（2）求证：平面平面 解：（1）由平面平面，且，‎ 所以平面，因为平面，‎ 所以.‎ ‎（2）由为线段中点， 可得，‎ 由平面，平面 可得平面平面 又平面平面，‎ 平面，且 即有平面，‎ 因为平面，‎ 所以平面平面.‎