北京市昌平区临川育人学校2017届高三上学期期末物理试卷 21页

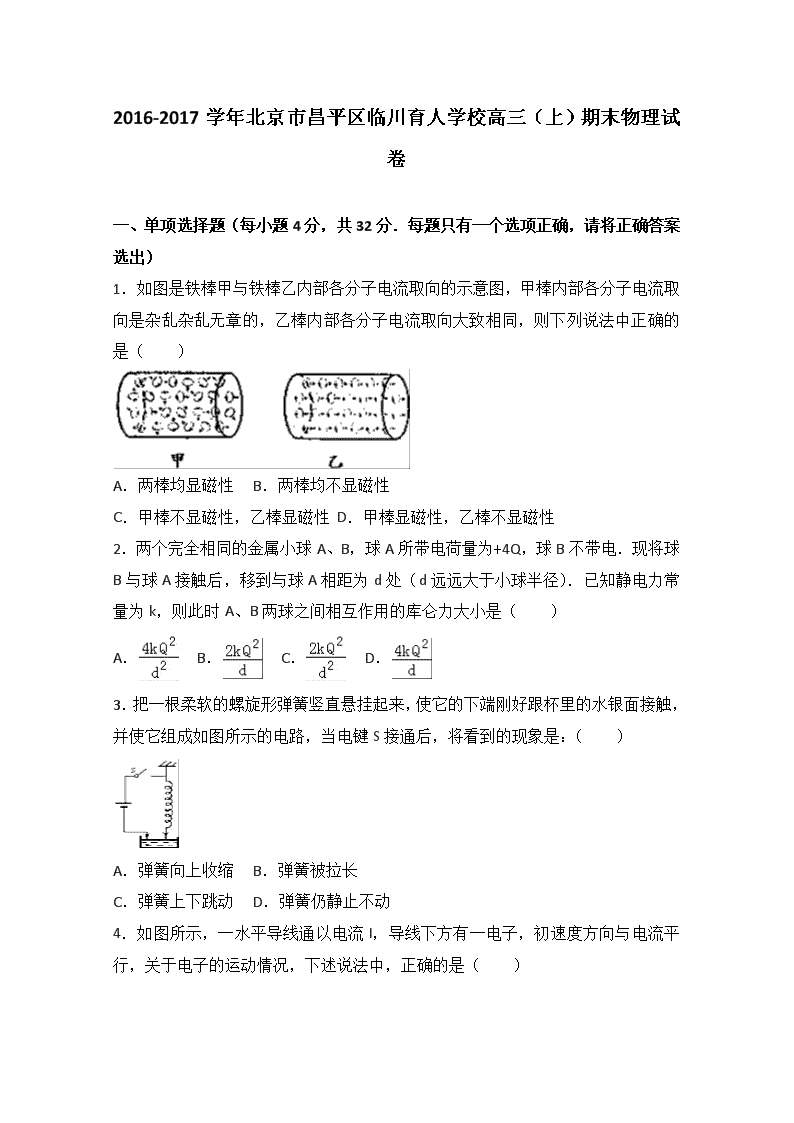
2016-2017 学年北京市昌平区临川育人学校高三（上）期末物理试 卷 　 一、单项选择题（每小题 4 分，共 32 分．每题只有一个选项正确，请将正确答案 选出） 1．如图是铁棒甲与铁棒乙内部各分子电流取向的示意图，甲棒内部各分子电流取 向是杂乱杂乱无章的，乙棒内部各分子电流取向大致相同，则下列说法中正确的 是（　　） A．两棒均显磁性 B．两棒均不显磁性 C．甲棒不显磁性，乙棒显磁性 D．甲棒显磁性，乙棒不显磁性 2．两个完全相同的金属小球 A、B，球 A 所带电荷量为+4Q，球 B 不带电．现将球 B 与球 A 接触后，移到与球 A 相距为 d 处（d 远远大于小球半径）．已知静电力常 量为 k，则此时 A、B 两球之间相互作用的库仑力大小是（　　） A． B． C． D． 3．把一根柔软的螺旋形弹簧竖直悬挂起来，使它的下端刚好跟杯里的水银面接触， 并使它组成如图所示的电路，当电键 S 接通后，将看到的现象是：（　　） A．弹簧向上收缩 B．弹簧被拉长 C．弹簧上下跳动 D．弹簧仍静止不动 4．如图所示，一水平导线通以电流 I，导线下方有一电子，初速度方向与电流平 行，关于电子的运动情况，下述说法中，正确的是（　　） A．沿路径 a 运动，其轨道半径越来越大 B．沿路径 a 运动，其轨道半径越来越小 C．沿路径 b 运动，其轨道半径越来越小 D．沿路径 b 运动，其轨道半径越来越大 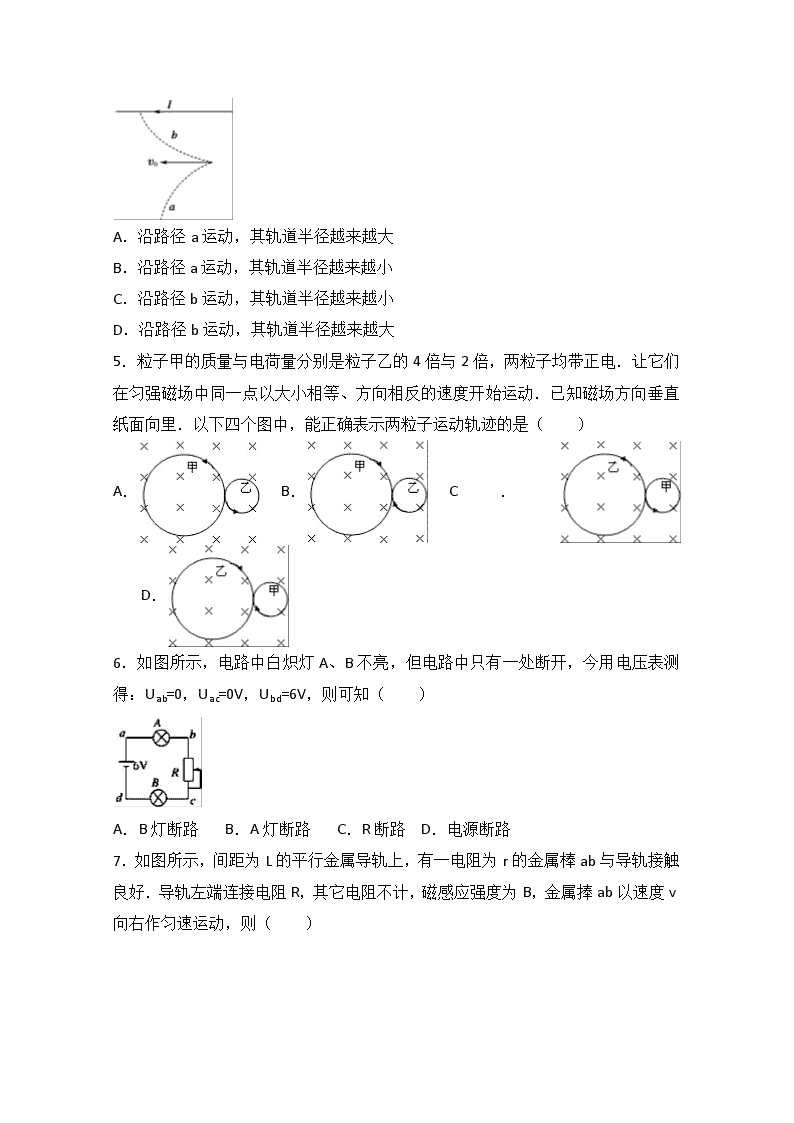5．粒子甲的质量与电荷量分别是粒子乙的 4 倍与 2 倍，两粒子均带正电．让它们 在匀强磁场中同一点以大小相等、方向相反的速度开始运动．已知磁场方向垂直 纸面向里．以下四个图中，能正确表示两粒子运动轨迹的是（　　） A． B． C ． D． 6．如图所示，电路中白炽灯 A、B 不亮，但电路中只有一处断开，今用电压表测 得：Uab=0，Uac=0V，Ubd=6V，则可知（　　） A．B 灯断路 B．A 灯断路 C．R 断路 D．电源断路 7．如图所示，间距为 L 的平行金属导轨上，有一电阻为 r 的金属棒 ab 与导轨接触 良好．导轨左端连接电阻 R，其它电阻不计，磁感应强度为 B，金属捧 ab 以速度 v 向右作匀速运动，则（　　） A．回路中电流为逆时针方向 B．电阻 R 两端的电压为 BLv C．ab 棒受到的安培力的方向向左 D．ab 棒中电流大小为 8．如图所示，在真空中坐标 xOy 面的 x＞0 区域内，有磁感应强度 B=1.0×10﹣2T 的匀强磁场，方向与 xOy 平面垂直，在 x 轴上的 P（10，0）点处有一放射源，在 xOy 平面内向各个方向发射速率为 v=1.0×105m/s 的带正电粒子，粒子的质量为 m=1.0×10﹣26kg，粒子带电量为 q=1.0×10﹣18C，则带电粒子能打到 y 轴上的范围 是（重力的影响不计）（　　） A．﹣10cm≤y≤10cm B．﹣10cm≤y≤ cm C． cm≤y≤ cm D． cm≤y≤10cm 　 二、多项选择题（每小题 6 分，共 24 分．每题有多个答案正确，请将正确答案选 出，全选对得 6 分，选不全得 3 分，有选错的不得分．） 9．下列说法正确的是（　　） A．奥斯特提出分子电流假说 B．法拉第采用了电场线的方法来描述电场 C．密立根用实验测定了电子的电量 D．纽曼和韦伯先后提出了电磁感应定律 10．回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电极相连 接的两个 D 形金属盒，两盒间的狭缝中形成的周期性变化的电场，使粒子在通过 狭缝时都能得到加速，两 D 形金属盒处于垂直于盒底的匀强磁场中，如图所示， 要增大带电粒子射出时的动能，则下列说法中正确的是（　　） A．增大匀强电场间的加速电压 B．增大磁场的磁感应强度 C．减小狭缝间的距离 D．减小 D 形金属盒的半径 　 三、实验题（共 18 分请按要求完成各题） 11．读出下列游标卡尺和螺旋测微器的示数 游标卡尺的示数为　　cm； 螺旋测微器的示数为　　cm． 12．某同学采用如图甲所示的电路测定电源电动势和内电阻，已知干电池的电动 势约为 1.5V，内阻约 2Ω，电压表（0～3V　约 3kΩ），电流表（0～0.6A　约 1.0Ω），滑动变阻器有 R1（10Ω　2A）和 R2 各一只． （1）实验中滑动变阻器应选用　　（选填“R1”或“R2”）． （2）在图乙中用笔画线代替导线连接实验电路． （3）在实验中测得多组电压和电流值，得到如图丙所示的 U﹣I 图象，由图可较准 确地求出电源电动势 E=　　V；内阻 r=　　Ω． 13．一束离子能沿入射直线方向通过互相垂直的匀强电场和匀强磁场区域，然后 进入磁感应强度为 B′的偏转磁场内做半径相同的匀速圆周运动（如图），则这束离 子必定有相同的　　，相同的　　． 　 四、计算题（共 32 分，写出必要的解题步骤） 14．某一用直流电动机提升重物的装置，如图所示，重物质量 m=50kg，电源的电 压为 U=110V，不计电源内阻及各处摩擦，当电动机以 v=0.90m/s 的恒定速度向上 提升重物时，电阻中的电流 I=5A，由此可知电动机的线圈的电阻 R 为多少？ 15．如图所示，ABCD 是一个正方形的匀强磁场区域，由静止开始经相同电压加速 后的甲、乙两种带电粒子，分别从 A、B 两点射入磁场，结果均从 C 点射出，则它 们的速率 v 甲：v 乙为多大？，它们通过该磁场所用的时间 t 甲：t 乙为多大？ 16．如图所示，有一对平行金属板，板间加有恒定电压；两板间有匀强磁场，磁 感应强度大小为 B0，方向垂直于纸面向里．金属板右下方以 MN、PQ 为上、下边 界，MP 为左边界的区域内，存在垂直纸面向外的匀强磁场，磁场宽度为 d，MN 与下极板等高，MP 与金属板右端在同一竖直线上．一电荷量为 q、质量为 m 的正 离子，以初速度 v0 沿平行于金属板面、垂直于板间磁场的方向从 A 点射入金属板 间，不计离子的重力． （1）已知离子恰好做匀速直线运动，求金属板间电场强度的大小； （2）若撤去板间磁场 B0，已知离子恰好从下极板的右侧边缘射出电场，方向与水 平方向成 30°角，求 A 点离下极板的高度； （3）在（2）的情形中，为了使离子进入磁场运动后从边界 MP 的 P 点射出，磁场 的磁感应强度 B 应为多大？ 　 2016-2017 学年北京市昌平区临川育人学校高三（上）期 末物理试卷 参考答案与试题解析 　 一、单项选择题（每小题 4 分，共 32 分．每题只有一个选项正确，请将正确答案 选出） 1．如图是铁棒甲与铁棒乙内部各分子电流取向的示意图，甲棒内部各分子电流取 向是杂乱杂乱无章的，乙棒内部各分子电流取向大致相同，则下列说法中正确的 是（　　） A．两棒均显磁性 B．两棒均不显磁性 C．甲棒不显磁性，乙棒显磁性 D．甲棒显磁性，乙棒不显磁性 【考点】分子电流假说． 【分析】当分子电流取向大致一致时，铁棒对外会显示磁性，而分子电流取向杂 乱杂乱无章时，磁性抵消，对外不显示磁性． 【解答】解：根据安培的分子电流假说可知，分子电流使每个分子相当于一个小 磁针．甲铁棒中各分子电流取向是杂乱杂乱无章的，磁性抵消，对外不显示磁性； 乙棒内部各分子电流取向大致相同，分子电流的磁性增强，对外显示磁性，故 C 正确． 故选：C 　 2．两个完全相同的金属小球 A、B，球 A 所带电荷量为+4Q，球 B 不带电．现将球 B 与球 A 接触后，移到与球 A 相距为 d 处（d 远远大于小球半径）．已知静电力常 量为 k，则此时 A、B 两球之间相互作用的库仑力大小是（　　） A． B． C． D． 【考点】库仑定律． 【分析】当 A 带电荷量为 4Q，B 带电荷量为 0，A、B 球相互接触后放回原处，距 离为 d，电荷先中和再平分，再根据库仑定律得到求解． 【解答】解：接触后两球将电量平分，即： =2Q， 再由库仑定律，得 =4 ，故 A 正确，BCD 错误． 故选：A 　 3．把一根柔软的螺旋形弹簧竖直悬挂起来，使它的下端刚好跟杯里的水银面接触， 并使它组成如图所示的电路，当电键 S 接通后，将看到的现象是：（　　） A．弹簧向上收缩 B．弹簧被拉长 C．弹簧上下跳动 D．弹簧仍静止不动 【考点】通电直导线和通电线圈周围磁场的方向． 【分析】当弹簧中通电流时，弹簧的每一圈导线都是一个线圈，都有N 极和 S 极， 根据安培定则判断每一线圈的下端都是 N 极，上端都是 S 极，根据异名磁极相互 吸引，弹簧缩短，弹簧离开水银面，电路断开，弹簧中没有电流，各线圈之间失 去吸引作用，弹簧恢复原状，弹簧下落到水银面接通电路，重复上面的现象． 【解答】解：当有电流通过弹簧时，构成弹簧的每一圈导线周围都产生了磁场， 根据安培定则知，各圈导线之间都产生了相互的吸引作用，弹簧就缩短了，当弹 簧的下端离开水银后，电路断开，弹簧中没有了电流，各圈导线之间失去了相互 吸引力，弹簧又恢复原长，使得弹簧下端又与水银接触，弹簧中又有了电流，开 始重复上述过程． 故选：C． 　 4．如图所示，一水平导线通以电流 I，导线下方有一电子，初速度方向与电流平 行，关于电子的运动情况，下述说法中，正确的是（　　） A．沿路径 a 运动，其轨道半径越来越大 B．沿路径 a 运动，其轨道半径越来越小 C．沿路径 b 运动，其轨道半径越来越小 D．沿路径 b 运动，其轨道半径越来越大 【考点】带电粒子在匀强磁场中的运动；通电直导线和通电线圈周围磁场的方 向． 【分析】先用安培定则判断出导线下方的磁场方向及分布情况，再由左手定则判 断电子运动时的受力方向，结合半径公式 可知半径的变化情况，从而得出正 确选项． 【解答】解：由安培定则可知，导线下方的磁场方向垂直纸面向外，且离导线越 远，磁场越弱，如图所示，电子初速度方向与电流方向相同，由左手定则可知受 到的洛伦兹力方向向下，由远离导线的方向磁场减弱，由 可知电子的运动半 径越大，所以选项 A 正确． 故选：A 　 5．粒子甲的质量与电荷量分别是粒子乙的 4 倍与 2 倍，两粒子均带正电．让它们 在匀强磁场中同一点以大小相等、方向相反的速度开始运动．已知磁场方向垂直 纸面向里．以下四个图中，能正确表示两粒子运动轨迹的是（　　） A． B． C ． D． 【考点】带电粒子在匀强磁场中的运动；牛顿第二定律；向心力；左手定则． 【分析】由洛仑兹力充当向心力可求得两粒子的半径关系，则由图可知两粒子的 轨迹图；由左手定则可判断粒子的运动方向． 【解答】解：两粒子均带正电，以大小相等的速度在磁场中向相反的方向运动， 都是由洛伦兹力充当粒子做圆周运动的向心力．所以有 ，得到 ，因 为粒子甲的质量与电荷量分别是粒子乙的 4 倍与 2 倍，所以甲的半径为乙半径的 2 倍．根据左手定则，甲粒子做圆周运动的洛伦兹力指向圆心，运动方向一定为逆 时针，所以 A 正确． 故选 A． 　 6．如图所示，电路中白炽灯 A、B 不亮，但电路中只有一处断开，今用电压表测 得：Uab=0，Uac=0V，Ubd=6V，则可知（　　） A．B 灯断路 B．A 灯断路 C．R 断路 D．电源断路 【考点】闭合电路的欧姆定律． 【分析】电路中只有一处断开，连接在一起的导体为等势体，根据各部分的电压 与电源电压的关系，判断故障所在位置． 【解答】解： A、由于电路中无电流，根据欧姆定律可知，连接在一起的导体电压为零，是一个 等势体，故凡未断开的灯丝及电阻器两端的电压应为零，相应电压表示数为零．由 题，Uab=0，Uac=0V，说明 A 灯、R 是完好的．由于 Ubd=6V，B 灯两端的电势分别 等于电源两极间的电势，说明 B 灯断路．故 A 正确，BC 错误． D、因为 Ubd=6V，所以电源不可能断路．故 D 错误． 故选 A 　 7．如图所示，间距为 L 的平行金属导轨上，有一电阻为 r 的金属棒 ab 与导轨接触 良好．导轨左端连接电阻 R，其它电阻不计，磁感应强度为 B，金属捧 ab 以速度 v 向右作匀速运动，则（　　） A．回路中电流为逆时针方向 B．电阻 R 两端的电压为 BLv C．ab 棒受到的安培力的方向向左 D．ab 棒中电流大小为 【考点】导体切割磁感线时的感应电动势；安培力；右手定则． 【分析】导体棒向右运动时切割磁感线产生逆时针方向的感应电流，导体棒 ab 相 当于电源，外电路为电阻 R，根据左手定则以可求出 ab 棒安培力的方向，根据闭 合电路欧姆定律可求出回路中感应电流的大小． 【解答】解：A、根据右手定责（或楞次定律）可知回路中的电流方向为逆时针的， 故 A 正确； B、感应电动势为：E=BLv，电阻 R 两端的电压为路端电压为： ，故 B 错误； C、根据左手定则可知 ab 棒受到的安培力的方向向左，故 C 正确； D、回路中的电流为： ，故 D 错误． 故选 AC． 　 8．如图所示，在真空中坐标 xOy 面的 x＞0 区域内，有磁感应强度 B=1.0×10﹣2T 的匀强磁场，方向与 xOy 平面垂直，在 x 轴上的 P（10，0）点处有一放射源，在 xOy 平面内向各个方向发射速率为 v=1.0×105m/s 的带正电粒子，粒子的质量为 m=1.0×10﹣26kg，粒子带电量为 q=1.0×10﹣18C，则带电粒子能打到 y 轴上的范围 是（重力的影响不计）（　　） A．﹣10cm≤y≤10cm B．﹣10cm≤y≤ cm C． cm≤y≤ cm D． cm≤y≤10cm 【考点】带电粒子在匀强磁场中的运动；牛顿第二定律；向心力． 【分析】带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿 第二定律求出粒子的轨道半径；作出粒子运动轨迹然后求出粒子打到 y 轴上的范 围． 【解答】解：洛伦兹力提供向心力，由牛顿第二定律得：qvB=m 解得粒子的轨道半径为： R= = m=0.1m， 由左手定则可知，粒子在磁场中沿逆时针做圆周运动，粒子的运动轨迹过 P 点， 粒子离开 P 点的最大距离为 2R，以 P 为圆心，2R 为半径做圆，交 y 轴与 A 点，A 是粒子打在 y 轴上的最远点，粒子在 y 轴负半轴上的最远点为 B，如图所示， 由几何知识得：OA= = =0.1 m=10 cm OB=R=0.1m=10cm，粒子打到 y 轴上的范围是﹣10cm～10 cm； 故选：B． 　 二、多项选择题（每小题 6 分，共 24 分．每题有多个答案正确，请将正确答案选 出，全选对得 6 分，选不全得 3 分，有选错的不得分．） 9．下列说法正确的是（　　） A．奥斯特提出分子电流假说 B．法拉第采用了电场线的方法来描述电场 C．密立根用实验测定了电子的电量 D．纽曼和韦伯先后提出了电磁感应定律 【考点】物理学史． 【分析】根据物理学史和常识解答，记住著名物理学家的主要贡献即可． 【解答】解：A、安培提出分子电流假说，故 A 错误； B、法拉第采用了电场线的方法来描述电场，故 B 正确； C、密立根用实验测定了电子的电量，故 C 正确； D、纽曼和韦伯先后提出了电磁感应定律，故 D 正确； 故选：BCD． 　 10．回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电极相连 接的两个 D 形金属盒，两盒间的狭缝中形成的周期性变化的电场，使粒子在通过 狭缝时都能得到加速，两 D 形金属盒处于垂直于盒底的匀强磁场中，如图所示， 要增大带电粒子射出时的动能，则下列说法中正确的是（　　） A．增大匀强电场间的加速电压 B．增大磁场的磁感应强度 C．减小狭缝间的距离 D．减小 D 形金属盒的半径 【考点】质谱仪和回旋加速器的工作原理． 【分析】回旋加速器利用电场加速和磁场偏转来加速粒子，根据洛伦兹力提供向 心力求出粒子射出时的速度，从而得出动能的表达式，看动能与什么因素有关． 【解答】解：当粒子从 D 形盒中出来时速度最大，根据 qvmB=m ，得 vm= ， 则动能 EK= mv2= ，知动能与加速的电压无关，与狭缝间的距离无关，与 磁感应强度大小和 D 形盒的半径有关，增大磁感应强度和 D 形盒的半径，可以增 加粒子的动能．故 B 正确，ABC 错误． 故选：B 　 三、实验题（共 18 分请按要求完成各题） 11．读出下列游标卡尺和螺旋测微器的示数 游 标 卡 尺 的 示 数 为 　 10.025 　 cm ； 螺 旋 测 微 器 的 示 数 为 　 0.5700 （0.5699﹣0.5701）　cm． 【考点】刻度尺、游标卡尺的使用；螺旋测微器的使用． 【分析】解决本题的关键掌握游标卡尺读数的方法，主尺读数加上游标读数，不 需估读．螺旋测微器的读数方法是固定刻度读数加上可动刻度读数，在读可动刻 度读数时需估读． 【解答】解：1、游标卡尺的主尺读数为 100mm，游标尺上第 5 个刻度和主尺上某 一 刻 度 对 齐 ， 所 以 游 标 读 数 为 5 × 0.05mm=0.25mm ， 所 以 最 终 读 数 为 ： 100mm+0.25mm=100.25mm=10.025cm． 2、螺旋测微器的固定刻度为 5.5mm，可动刻度为 20.0×0.01mm=0.2000mm，所以 最终读数为 5.5mm+0.200mm=5.700mm=0.5700cm，由于需要估读，最后的结果可 以在 0.5699﹣0.5701 之间． 故答案为：（1）10.025 0.5700 （0.5699﹣0.5701） 　 12．某同学采用如图甲所示的电路测定电源电动势和内电阻，已知干电池的电动 势约为 1.5V，内阻约 2Ω，电压表（0～3V　约 3kΩ），电流表（0～0.6A　约 1.0Ω），滑动变阻器有 R1（10Ω　2A）和 R2 各一只． （1）实验中滑动变阻器应选用　R1　（选填“R1”或“R2”）． （2）在图乙中用笔画线代替导线连接实验电路． （3）在实验中测得多组电压和电流值，得到如图丙所示的 U﹣I 图象，由图可较准 确地求出电源电动势 E=　1.50　V；内阻 r=　1.94　Ω． 【考点】测定电源的电动势和内阻． 【分析】（1）滑动变阻器在电路中起到保护电路并调节电流作用，在限流接法中 取比内电阻大 10 左右即可．过大则难以调节；过小起不到应有的调节作用． （2）先串后并，并注意元件顺序，开关位置，且连线不能交叉． （3）由闭合电路欧姆定律可得出电压与电流的关系，结合数学关系可知图象的斜 率表示内阻，与纵坐标的交点表示电源的电动势． 【解答】解：（1）由题意可知，电源的内阻约为 1Ω，故为了易于调节，准确测量， 还有 R2 额定电流只有 0.1A，很容易烧坏，所以滑动变阻器应选小电阻 R1 ． （2）先串后并，并注意元件顺序，开关位置，且连线不能交叉，另注意电表+﹣ 接线柱，如下图所示． （3）由闭合电路欧姆定律可知：U=E﹣Ir； 即电动势与电流成一次函数关系，由数学知识可知，图象与纵坐标的交点为电源 的电动势； 图象的斜率表示内源内电阻； 故由图可得电动势为：E=1.50V，r= = ≈1.94Ω． 故答案为：（1）1；②电路图如图所示；（3）1.50；1.94． 　 13．一束离子能沿入射直线方向通过互相垂直的匀强电场和匀强磁场区域，然后 进入磁感应强度为 B′的偏转磁场内做半径相同的匀速圆周运动（如图），则这束离 子必定有相同的　速率　，相同的　比荷　． 【考点】带电粒子在匀强磁场中的运动；带电粒子在匀强电场中的运动． 【分析】通过互相垂直的匀强电场和匀强磁场区域，根据电场力与洛伦兹力平衡， 则有相同的速度大小；再由洛伦兹力提供向心力作匀速圆周运动，根据牛顿第二 定律，即可求解． 【解答】解：沿入射方向通过互相垂直的匀强电场和匀强磁场区域，则有电场力 与洛伦兹力平衡，即 qE=Bqv，解得：v= ；故说明粒子具有相同的速度； 当进入磁感应强度为 B 的偏转磁场内做半径相同的匀速圆周运动，则有：B′qv= ， 解得：R= ， 由于半径相同，则说明离子的比荷相同； 故答案为：速率；比荷． 　 四、计算题（共 32 分，写出必要的解题步骤） 14．某一用直流电动机提升重物的装置，如图所示，重物质量 m=50kg，电源的电 压为 U=110V，不计电源内阻及各处摩擦，当电动机以 v=0.90m/s 的恒定速度向上 提升重物时，电阻中的电流 I=5A，由此可知电动机的线圈的电阻 R 为多少？ 【考点】闭合电路中的能量转化；电功、电功率． 【分析】用直流电动机提升重物时，电动机消耗的电能转化为电动机的内能和提 升重物的机械能，根据能量守恒定律列出功率求解 R． 【解答】解：电动机消耗的总能量一部分用于提升重物的机械能，一部分消耗在 电动机线圈电阻发热上．根据能量守恒定律得 P 电=P 机+P 热， 其中 P 电=IU，P 机=mgv，P 热=I2R， 所以有 IU=mgv+I2R， 代入解得 R= =4Ω 答：电动机的线圈的电阻 R 为 4Ω． 　 15．如图所示，ABCD 是一个正方形的匀强磁场区域，由静止开始经相同电压加速 后的甲、乙两种带电粒子，分别从 A、B 两点射入磁场，结果均从 C 点射出，则它 们的速率 v 甲：v 乙为多大？，它们通过该磁场所用的时间 t 甲：t 乙为多大？ 【考点】带电粒子在匀强磁场中的运动． 【分析】根据粒子的半径大小，通过洛伦兹力提供向心力求出粒子的荷质比．结 合粒子在磁场中运动的周期公式比较两粒子在磁场中的运动时间关系． 【解答】解：（1）根据动能定理：qU= mv2， 得：v= 根据轨迹图可知，甲、乙两粒子的半径之比为 2：1， 根据 qvB=m 得： （2）粒子运动的周期： 与粒子运动的速度无关，它们通过该磁场所用的时间为： t 甲：t 乙为： 答：它们的速率 v 甲：v 乙为 2：1，它们通过该磁场所用的时间 t 甲：t 乙为 1：2． 　 16．如图所示，有一对平行金属板，板间加有恒定电压；两板间有匀强磁场，磁 感应强度大小为 B0，方向垂直于纸面向里．金属板右下方以 MN、PQ 为上、下边 界，MP 为左边界的区域内，存在垂直纸面向外的匀强磁场，磁场宽度为 d，MN 与下极板等高，MP 与金属板右端在同一竖直线上．一电荷量为 q、质量为 m 的正 离子，以初速度 v0 沿平行于金属板面、垂直于板间磁场的方向从 A 点射入金属板 间，不计离子的重力． （1）已知离子恰好做匀速直线运动，求金属板间电场强度的大小； （2）若撤去板间磁场 B0，已知离子恰好从下极板的右侧边缘射出电场，方向与水 平方向成 30°角，求 A 点离下极板的高度； （3）在（2）的情形中，为了使离子进入磁场运动后从边界 MP 的 P 点射出，磁场 的磁感应强度 B 应为多大？ 【考点】带电粒子在匀强磁场中的运动；带电粒子在匀强电场中的运动． 【分析】（1）离子做匀速直线运动时，电场力和洛仑兹力二力平衡，根据平衡条 件列式，即可求解电场强度的大小，由左手定则判断出洛兹力的方向，即可确定 电场强度的方向； （2）撤去板间磁场 B0，离子在电场中做类平抛运动，平行于极板做匀速直线运动， 垂直于极板做初速度为零的匀加速直线运动，根据速度的分解求出离子从 M 点射 出电场时的速度，由动能定理求解 A 点离下极板的高度； （3）根据题意画出离子的运动轨迹，根据几何知识求出轨迹半径，再由洛伦兹力 提供向心力，列式求解 B． 【解答】解：（1）设板间的电场强度为 E，离子做匀速直线运动，受到的电场力 和洛仑兹力平衡有： qE=qv0B0 解得：E=v0B0 ① 由左手定则可判断出洛仑兹力方向竖直向上，所以电场力的方向竖直向下，故场 强的方向竖直向下． （2）设 A 点离下极板的高度为 h，离子射出电场时的速度为 v，根据动能定理得： ② 离子在电场中做类平抛运动，水平分方向做匀速直线运动，则有 v= ③ 联立①②③解得：h= = ④ （3）设离子进入磁场后做匀速圆周运动的半径为 r，由几何关系得：r= = ⑤ 根据牛顿第二定律得：qvB=m ⑥ 联立③⑤⑥解得： ； 答：（1）金属板间电场强度的大小为 v0B0，方向竖直向下； （2）A 点离下极板的高度为 ； （3）磁场的磁感应强度 B 应为 ． 　 2017 年 2 月 16 日