- 451.00 KB
- 2021-04-15 发布
集宁一中东校区2019-2020学年第一学期第二次月考
高一年级数学试题
本试卷满分150分,考试时间120分钟
一、选择题 (共60分)
1.已知集合,,则( ).
A.{2,3,4} B. C.{3,4} D.
2.已知函数,若,则( ).
A.4 B.3 C.2 D.1
3.函数的单调递增区间为( ).
A.(2, 5) B.(-1, 2) C.(-∞, 2) D.(2,+∞)
4.若直线和没有公共点,则与的位置关系是( ).
A.相交 B.平行 C.异面 D.平行或异面
5.已知函数,则( ).
A.3 B.5 C.6 D.32
6.如图所示,四边形OABC是上底为2,下底为6,底角为45°的等腰梯形,用斜二测画法画出这个梯形的直观图O′A′B′C′,在直观图中梯形的面积为( ).
7.下列说法正确的是( ).
A. 三点确定一个平面
B. 四边形一定是平面图形
C. 梯形一定是平面图形
D. 平面α和平面β有不同在一条直线上的三个公共点
8.如图,在正方体中, 为线段的中点,则异面直线与所成角的大小为( )度.
A. 60 B. 45
C. 30 D. 15
9.设是定义域为的偶函数,且在单调递减,则( ).
A. B.
C. D.
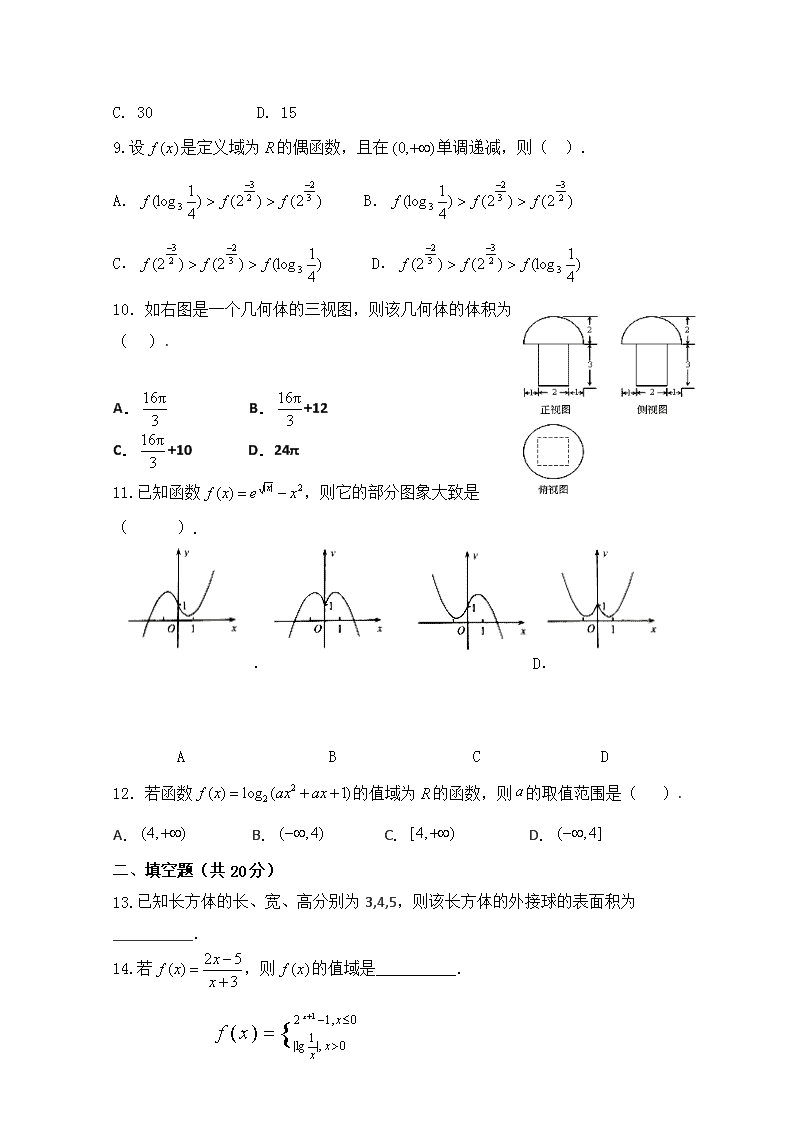
10.如右图是一个几何体的三视图,则该几何体的体积为( ).
A. B.+12
C.+10 D.24π
11.已知函数,则它的部分图象大致是
( ).
. D.
A B C D
12.若函数的值域为的函数,则的取值范围是( ).
A. B. C. D.
二、 填空题(共20分)
13.已知长方体的长、宽、高分别为3,4,5,则该长方体的外接球的表面积为__________.
14.若,则的值域是__________.
15. 已知函数 ,若函数有3个零点,则取值范围为____.
16. 有下列说法:①在圆柱的上、下底面的圆周上各取一点,则这两点连线的长度是母线的长度;②圆锥顶点与底面圆周上任意一点连线的长度是母线的长度;③圆柱的任意两条母线所在直线互相平行;④过球上任意两点有且只有一个大圆;其中正确的序号是_____.
三、 解答题(共70分)
17.(本题10分)底面边长为的正三棱锥,其表面展开图是正三角形,如图所示.
求:(1)的各边长;
(2)三棱锥的体积.
18.(本题12分)已知函数是指数函数,
(1)求的表达式;
(2)判断的奇偶性,并加以证明;
(3)解不等式:.
19.(本题12分)设函数恒有零点
(1)求的取值范围;
(2)如果有两个不同的零点,其倒数之和为-4,求的值.
20.(本题12分)国庆期间,某旅行社组团去风景区旅游,若旅行团人数不超过20人,每人需交费用800元;若旅行团人数超过20人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数60人为止.旅行社需支付各种费用共计10000元.
(1)写出每人需交费用S关于旅行团人数的函数;
(2)旅行团人数x为多少时,旅行社可获得最大利润?最大利润是多少?
21.(本题12分)已知,且.
(1)当时,解不等式;
(2)在恒成立,求实数的取值范围.
22.(本题12分)已知函数,它的反函数图象过点.
(1)求实数的值;
(2)若存在使得 成立,求实数的取值范围.