- 623.53 KB
- 2021-04-15 发布
天津市第一中学2017—2018学年度高三年级二月考试卷
数 学(文史类)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A. {0,1,2} B. {1,2} C. {0} D. {0,1}
【答案】D
【解析】集合A={0,1,2},B={x|x2﹣5x+4<0}={x|1<x<4},
故选:B.
点睛:本题考查集合的运算,主要是交集、补集的求法,考查真子集的求法,属于基础题.
2. 是的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
【答案】A
【解析】因为,所以,两边同乘以得:,当时,可得,推不出,综上是的充分不必要条件,故选A.
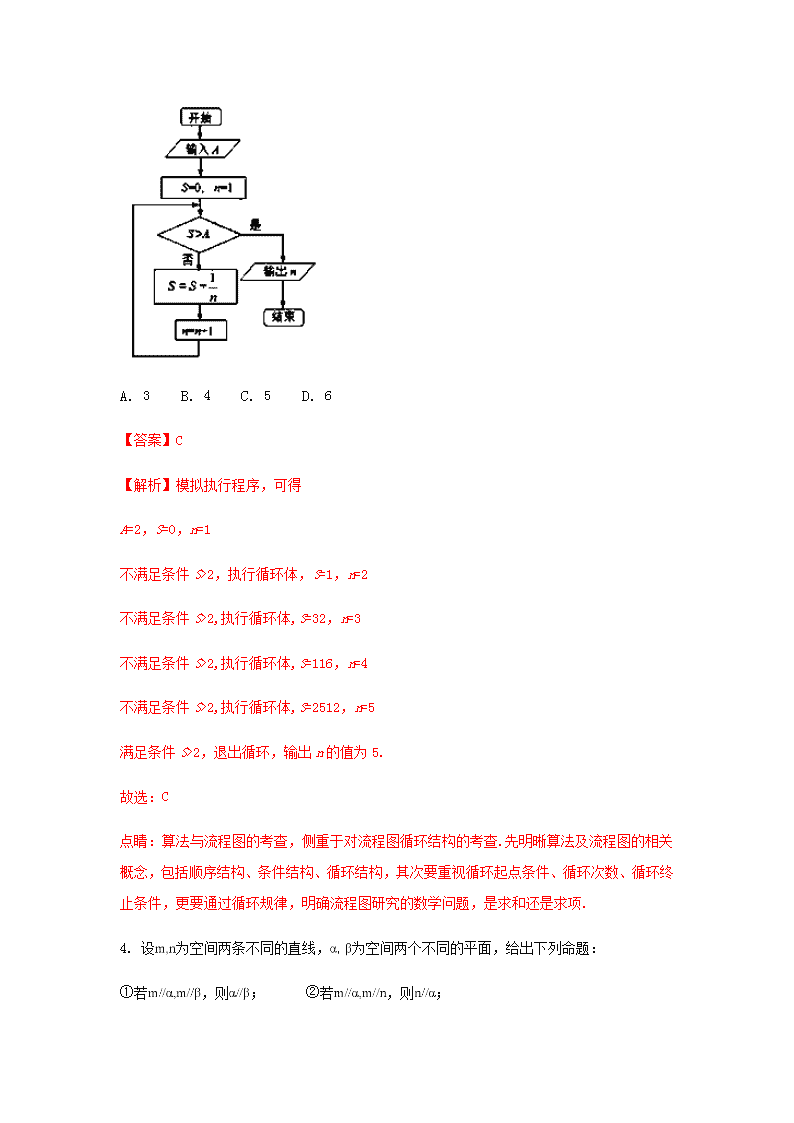
3. 执行如图所示的程序框图,若输入的值为 2,则输出的值为( )
A. 3 B. 4 C. 5 D. 6
【答案】C
【解析】模拟执行程序,可得
A=2,S=0,n=1
不满足条件S>2,执行循环体,S=1,n=2
不满足条件S>2,执行循环体,S=32,n=3
不满足条件S>2,执行循环体,S=116,n=4
不满足条件S>2,执行循环体,S=2512,n=5
满足条件S>2,退出循环,输出n的值为5.
故选:C
点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括顺序结构、条件结构、循环结构,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.
4. 设为空间两条不同的直线,为空间两个不同的平面,给出下列命题:
①若,则; ②若,则;
③若,则; ④若,则.
其中所有正确命题的序号是( )
A. ②④ B. ③④ C. ①② D. ①③
【答案】B
【解析】对于①,若m∥α,m∥β,则α与β可能相交;故①错误;
对于②,若m∥α,m∥n则n可能在α内;故②错误;
对于③,若m⊥α,m∥β,根据线面垂直和线面平行的性质定理以及面面垂直的判定定理得到α⊥β;故③正确;
对于④,若m⊥α,α∥β,则根据线面垂直的性质定理以及面面平行的性质定理得到m⊥β;故④正确;故选B.
点睛:本题考查了空间线面平行、线面垂直面面垂直的性质定理和判定定理的运用;熟练掌握定理是关键.
5. 已知奇函数在上是增函数,.若,,则的大小关系为( )
A. B. C. D.
【答案】C
【解析】因为是奇函数且在上是增函数,所以在时,,
从而是上的偶函数,且在上是增函数,
,
,又,则,所以即,
,
所以,故选C.
【考点】 指数、对数、函数的单调性
【名师点睛】比较大小是高考常见题,指数式、对数式的比较大小要结合指数函数、对数函数,借助指数函数和对数函数的图象,利用函数的单调性进行比较大小,特别是灵活利用函数的奇偶性和单调性数形结合不仅能比较大小,还可以解不等式.
6. 已知函数当时,,则的取值范围是( )
A. B. C. D.
【答案】A
【解析】∵当x1≠x2时,<0,∴f(x)是R上的单调减函数,
∵f(x)=,∴,
∴0<a≤,故选:A.
7. 设函数,若在区间上单调,且,则的最小正周期为( )
A. B. C. D.
【答案】D
【解析】∵函数f(x)=sin(ωx+φ),A>0,ω>0,若f(x)在区间[,]上单调,
∴﹣≤==,即≤,∴0<ω≤3.
∵f()=f()=﹣f(),∴x==,为f(x)=sin(ωx+φ)的一条对称轴,
且(,0)即(,0)为f(x)=sin(ωx+φ)的一个对称中心,
∴=•=﹣=,解得ω=2∈(0,3],∴T==π,故选:D.
点睛:本题考查三角函数的周期性及其求法,确定x=与(,0)为同一周期里面相邻的对称轴与对称中心是关键,也是难点,属于难题.
8. 已知均为正数,且,则的最小值为( )
A. 6 B. 7 C. 8 D. 9
【答案】B
【解析】∵a,b均为正数,且ab﹣a﹣2b=0,∴=1.
则=+b2﹣1.
∴(+b2)(1+1)≥≥16,当且仅当a=4,b=2时取等号.
∴+b2≥8,
∴=+b2﹣1≥7.故选B.
点睛:本题考查“乘1法”、基本不等式的性质、柯西不等式,考查了推理能力与计算能力,属于中档题.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
9. 已知是实数,是纯虚数,则 ___________.
【答案】
【解析】设=bi(b≠0),则a﹣i=(2+i)•bi=﹣b+2bi,∴,解得a=.
故填:.
10. 曲线在点处的切线与两坐标轴围成的三角形的面积是__________.
【答案】
【解析】,
∴在点P(1,0)处的切线斜率为k=1,
∴在点P(1,0)处的切线l为y﹣0=x﹣1,即y=x﹣1,
∵y=x﹣1与坐标轴交于(0,﹣1),(1,0).
∴切线y=x﹣1与坐标轴围成的三角形面积为S=×1×1=.故答案为:.
点睛:本题考查了导数的运用:求切线的方程,考查导数的几何意义,以及三角形的面积计算,属于基础题.
11. 如图是一个几何体的三视图,则该几何体的体积为_________.
【答案】
【解析】根据三视图知几何体是组合体,中间是长宽高分别为1,2,2的长方体、两边是两个半圆锥,半径为1,高为2,
∴该几何体的体积V=1×2×2+π•12•2=4+,故答案为4+.
点睛:本题考查由三视图求几何体的体积,以及几何体的体积公式,考查空间想象能力,三视图正确复原几何体是解题的关键.
12. 圆心在直线,且与直线相切于点的圆的标准方程为__________.
【答案】
【解析】∵圆心在直线y=﹣4x上,
设圆心C为(a,﹣4a),圆与直线x+y﹣1=0相切于点P(3,﹣2),
则kPC==1,∴a=1.即圆心为(1,﹣4).
r=|CP|==2,∴圆的标准方程为(x﹣1)2+(y+4)=8.
故答案为:(x﹣1)2+(y+4)=8.
点睛:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,以及直线的点斜式方程,当直线与圆相切时,圆心到切线的距离等于圆的半径.属于基础题.
13. 在中,已知,若点满足,且,则实数的值为__________.
【答案】1或
【解析】中,,点满足,∴,
∴,又,整理得,解得或,故答案为 或.
14. 已知函数若函数有三个零点,则实数的取值范围为__________.
【答案】
【解析】函数,若函数有三个零点,
就是与有3个交点,
,画出两个函数的图象如图:
,
当x<0时,,当且仅当x=−1时取等号,此时−b>6,可得b<−6;
当时,当时取得最大值,满足条件的.
综上,.
给答案为:.
点睛:已知函数有零点求参数常用的方法和思路:
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成函数的值域问题解决;
(3)数形结合法:先对解析式变形,在同一个平面直角坐标系中,画出函数的图像,然后数形结合求解.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
15. 在中,角所对的边分别为,且,已知,,.
(I)求和的值
(II)求的值
【答案】(1) (2)
【解析】试题分析:(1)由向量的数量积运算及三角形余弦定理可求得a,c的关系式,解方程可求得其值;由正弦定理可求得角B,C的正余弦值,代入公式可求得的值
试题解析:(1)由,得:,又,所以.
由余弦定理,得.又,所以.
解,得或.因为,∴.
(2)在中,.
由正弦定理,得,又因为,所以为锐角,
因此.
于是.
考点:正余弦定理解三角形及三角函数基本公式
16. 某公司计划在甲、乙两个电视台做总时间不超过 300 分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.设该公司在甲、乙两个电视台做广告的时间分别为分钟和分钟.
(Ⅰ)用列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)该公司如何分配在甲、乙两个电视台做广告的时间使公司的收益最大,并求出最大收益是多少?
【答案】(1)详见解析(2) 该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告使公司的收益最大,最大收益是70万元.
【解析】试题分析:(I)根据广告费用和收益列出约束条件,作出可行域;
(II)列出目标函数z=3000x+2000y,根据可行域判断最优解的位置,列方程组解出最优解得出最大收益.
试题解析:(I)设该公司在甲、乙两个电视台做广告的时间分别为分钟和分钟,则,满足的数学关系式为
该二次元不等式组等价于
做出二元一次不等式组所表示的平面区域
(II)设公司的收益为元,则目标函数为:
考虑,将它变形为.
这是斜率为,随变化的一族平行直线,当截距最大,即最大.
又因为满足约束条件,所以由图可知,
当直线经过可行域上的点时,截距最大,即最大.
解方程组得,
代入目标函数得.
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告使公司的收益最大,最大收益是70万元.
17. 如图,边长为的正方形与梯形所在的平面互相垂直,其中
的中点.
(Ⅰ)证明:平面
(Ⅱ)求二面角的正切值
(Ⅲ)求与平面所成角的余弦值
【答案】(1) (2)
【解析】试题分析:(Ⅰ)推导出OM∥AC,由此能证明OM||平面ABCD.
(Ⅱ)取AB中点H,连接DH,则∠EHD为二面角D﹣AB﹣E的平面角,由此能求出二面角D﹣AB﹣E的正切值.
(Ⅲ)推导出BD⊥DA,从而BD⊥平面ADEF,由此得到∠BFD的余弦值即为所求.
试题解析:
(I)分别为的中点
平面 平面
平面
(II)取中点,连接
, 又
为二面角的平面角
又
∵平面平面,平面平面平面
平面 的余弦值即为所求
在中,
与平面所成角的余弦值为
点睛:本题考查线面平行的证明,考查二面角的正切值的求法,考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.
18. 已知数列的前项和为,
(Ⅰ)求数列的通项公式
(II)设,为的前项和,求
【答案】(1)详见解析(2)
【解析】试题分析:(1)利用递推关系与等比数列的通项公式即可得出;
(2)当n为奇数时,bn==;当n为偶数时,bn==.
分别利用“裂项求和”、“错位相减法”即可得出.
试题解析:(1)
又
∴数列是以2为首项,公比为2的等比数列
由(1)知
所以
设,
则,
两式相减得,
整理得,所以.
点睛:本题考查了递推关系、等比数列的通项公式前n项和公式、“裂项求和”方法、“错位相减法”,考查了推理能力与计算能力,属于中档题.
19. 已知数列中,
(I)求证:数列是等比数列
(II)求数列的通项公式
(III)设,若,使成立,求实数的取值范围.
【答案】(1)详见解析(2)(3)
【解析】试题分析:(I)由,变形为利用等比数列的定义即可证明.
(II)由(I)可得:,利用“累加求和”方法、等比数列的求和公式即可得出.
(III),可得.利用“裂项求和”方法可得Sn,再利用数列的单调性、不等式的解法即可得出.
试题解析:
(I)证明:,
.
,,.
∴数列是首项、公比均为2的等比数列
(II)解:是等比数列,首项为2,通项,
故
,当时,符合上式,
∴数列的通项公式为
(III)解:,
故
若,使成立,由已知,有,解得,所以的取值范围为
点睛:本题考查了递推关系、等比数列的定义及其通项公式、“裂项求和”方法、“累加求和”方法、数列的单调性、不等式的解法,考查了推理能力与计算能力,属于难题.
20. 已知函数,其中为自然对数的底数,
(I)若,函数
①求函数的单调区间
②若函数的值域为,求实数的取值范围
(II)若存在实数,使得,且,求证:
【答案】(1)①详见解析②实数的取值范围是;(2);
【解析】试题分析:(1)①求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
②求出函数的导数,通过讨论m的范围得到函数的值域,从而确定m的具体范围即可;
(2)求出函数f(x)的导数,得到a>0且f(x)在(﹣∞,]递减,在[,+∞)递增,设,则有
,根据函数的单调性得到关于m的不等式组,解出即可.
试题解析:
(1)当时,.
①.
由得,由得.
所以函数的单调增区间为,单调减区间为.
②
当时,,所以在区间上单调递减;
当时,,所以在区间上单调递增.
在上单调递减,值域为,
因为的值域为,所以,
即.
由①可知当时,,故不成立.
因为在上单调递减,在上单调递增,且
所以当时,恒成立,因此.
当时,在上单调递减,在上单调递增,
所以函数在上的值域为,即.
在上单调递减,值域为.
因为的值域为,所以,即.
综合1°,2°可知,实数的取值范围是.
(2).
若时,,此时在上单调递增.
由可得,与相矛盾,
同样不能有.
不妨设,则有.
因为在上单调递减,在上单调递增,且,
所以当时,.
由,且,可得
故.
又在单调递减,且,所以,
所以,同理.
即解得,
所以.
点睛:本题考查函数的单调性极值及恒成立问题,涉及函数不等式的证明,综合性强,难度大,属于难题.处理导数大题时,注意分层得分的原则,力争第一二问答对,第三问争取能写点,一般涉及求函数单调性及极值时,比较容易入手,求导后注意分类讨论,对于恒成立问题一般要分离参数,然后利用函数导数求函数的最大值或最小值,对于含有不等式的函数问题,一般要构造函数,利用函数的单调性来解决,但涉及技巧比较多,需要多加体会.