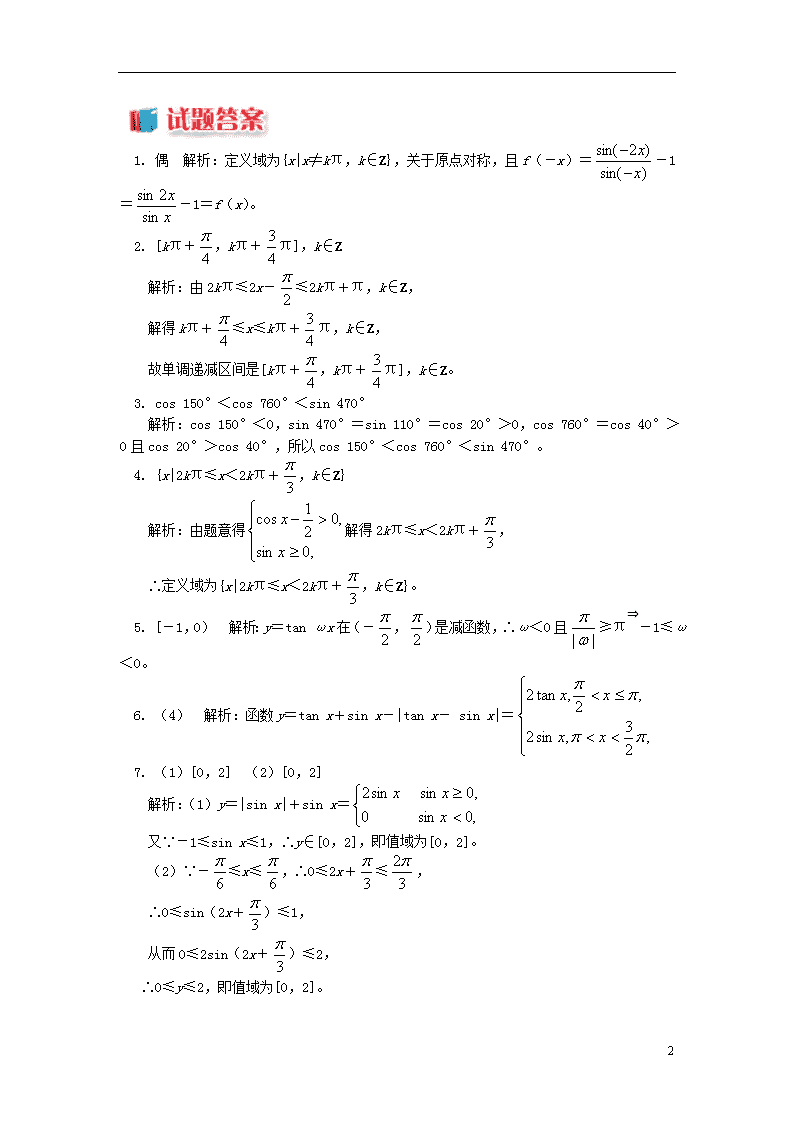- 180.00 KB
- 2021-04-14 发布
三角函数的图象和性质
(答题时间:25分钟)
1. 函数f(x)=-1是________函数。(填“奇”或“偶”)
2. 函数y=cos(2x-)的单调减区间是________。
*3. 将cos 150°,sin 470°,cos 760°按从小到大排列为________。
**4. 函数f(x)=lg(cos x-)+的定义域是________。
**5. 已知函数y=tan ωx在(-,)内是减函数,则ω的取值范围是________。
*6. 函数y=tan x+sin x-|tan x-sin x|在区间(,)内的图象是下图中的________。
*7. 求下列函数的值域:
(1)y=|sin x|+sin x;
(2)y=2sin(2x+),x∈[-,]。
**8. 求下列函数的定义域。
(1)y=;
(2)y=+lg(1-tan x)。
**9. 已知≤x≤,f(x)=tan2x+2tan x+2,求f(x)的最值及相应的x值。
3
1. 偶 解析:定义域为{x|x≠kπ,k∈Z},关于原点对称,且f(-x)=-1=-1=f(x)。
2. [kπ+,kπ+π],k∈Z
解析:由2kπ≤2x-≤2kπ+π,k∈Z,
解得kπ+≤x≤kπ+π,k∈Z,
故单调递减区间是[kπ+,kπ+π],k∈Z。
3. cos 150°<cos 760°<sin 470°
解析:cos 150°<0,sin 470°=sin 110°=cos 20°>0,cos 760°=cos 40°>0且cos 20°>cos 40°,所以cos 150°<cos 760°<sin 470°。
4. {x|2kπ≤x<2kπ+,k∈Z}
解析:由题意得解得2kπ≤x<2kπ+,
∴定义域为{x|2kπ≤x<2kπ+,k∈Z}。
5. [-1,0) 解析:y=tan ωx在(-,)是减函数,∴ω<0且≥π⇒-1≤ω<0。
6. (4) 解析:函数y=tan x+sin x-|tan x- sin x|=
7. (1)[0,2] (2)[0,2]
解析:(1)y=|sin x|+sin x=
又∵-1≤sin x≤1,∴y∈[0,2],即值域为[0,2]。
(2)∵-≤x≤,∴0≤2x+≤,
∴0≤sin(2x+)≤1,
从而0≤2sin(2x+)≤2,
∴0≤y≤2,即值域为[0,2]。
3
8. (1)(kπ-,kπ+],k∈Z (2){x|kπ≤x<kπ+,k∈Z}
解析:(1)由-tan x≥0,
得tan x≤,
在(-,)内满足不等式的范围是(-,],
又y=tan x的周期为π,
故原函数的定义域为(kπ-,kπ+],k∈Z。
(2)函数y=+lg(1-tan x)有意义,等价于所以0≤tan x<1。由正切曲线可得kπ≤x<kπ+,k∈Z,故原函数的定义域为{x|kπ≤x<kπ+,k∈Z}。
9. 当时,的最小值是1;当x=时,f(x)的最大值是5。
解析:∵-≤x≤,
∴-≤tan x≤1,
f(x)=tan2x+2tan x+2
=(tan x+1)2+1,
当tan x=-1,即x=-时,f(x)有最小值1;当tan x=1,即x=时,f(x)有最大值5。
3
相关文档
- 河北省中国第二十冶金建设公司综合2021-04-14 23:05:445页
- 2020版同步人教版高中历史必修3培2021-04-14 23:05:033页
- 2019-2020学年新教材高中语文第七2021-04-14 23:04:047页
- 2020学年度高中历史 第二单元第8课2021-04-14 23:04:0418页
- 高中化学 第三章 第三节 乙醇 第12021-04-14 23:02:076页
- 关于高中毕业生自我鉴定范文2021-04-14 23:01:582页
- 河南省郑州市示范性高中2021届高三2021-04-14 23:01:533页
- 其他(心得)之新课程透析高中语文课改2021-04-14 23:01:008页
- 四川省成都七中2020届高三高中毕业2021-04-14 22:59:0712页
- 高中学生自拟个人学习计划2021-04-14 22:58:212页