人教版七年级上册数学第四章测试题（含答案） 6页

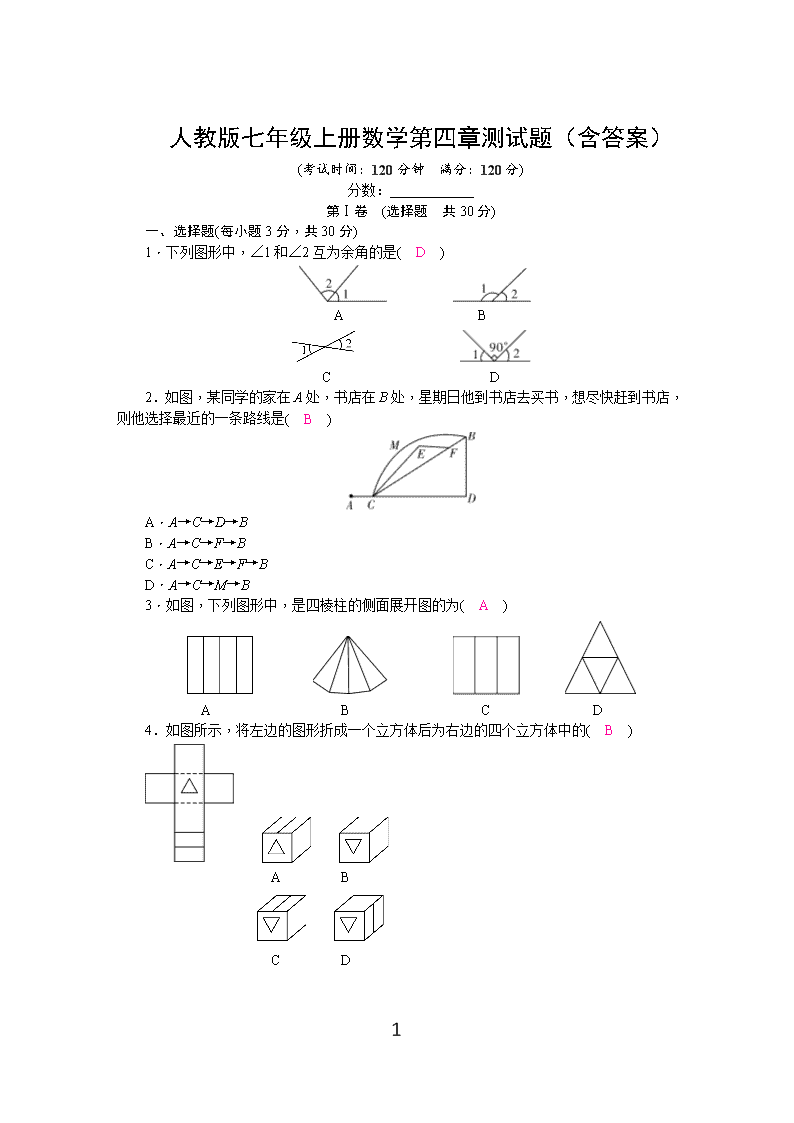
人教版七年级上册数学第四章测试题（含答案）‎ ‎(考试时间：120分钟　满分：120分)‎ 分数：____________‎ 6‎ 第Ⅰ卷　(选择题　共30分)‎ 一、选择题(每小题3分，共30分)‎ ‎1．下列图形中，∠1和∠2互为余角的是(　D　)‎ ‎　　　　　　　　　　　 ‎ A B ‎ ‎ C D ‎2．如图，某同学的家在A处，书店在B处，星期日他到书店去买书，想尽快赶到书店，则他选择最近的一条路线是(　B　)‎ A．A→C→D→B B．A→C→F→B C．A→C→E→F→B D．A→C→M→B ‎3．如图，下列图形中，是四棱柱的侧面展开图的为(　A　)‎ ‎ 　 　 　‎ A B C D ‎4．如图所示，将左边的图形折成一个立方体后为右边的四个立方体中的(　B　)‎ ‎　　　　‎ A B ‎　　　　　　 　　‎ C D 6‎ ‎5．下列判断中错误的有(　D　)‎ ‎①延长射线OA；‎ ‎②直线比射线长，射线比线段长；‎ ‎③如果线段PA＝PB，那么点P是线段AB的中点；‎ ‎④连接两点间的线段，叫做两点间的距离．‎ A．0个 B．2个 C．3个 D．4个 ‎6．如图，下列说法中不正确的是(　D　)‎ A．OC的方向是南偏东30°‎ B．OA的方向是北偏东45°‎ C．OB的方向是西偏北30°‎ D．∠AOB的度数是75°‎ ‎7．以长方形3 cm长的边所在直线为轴旋转一周形成圆柱体甲，以长方形2 cm长的边所在直线为轴旋转一周形成圆柱体乙，记两个圆柱的体积为V甲，V乙，侧面积为S甲，S乙，则下列式子中正确的是(　A　)‎ A．V甲＜V乙，S甲＝S乙 B．V甲＞V乙，S甲＞S乙 C．V甲＝V乙，S甲＝S乙 D．V甲＞V乙，S甲＜S乙 ‎8．★点P，Q在线段AB中点的同一侧，点P将AB分为2∶3的两段，点Q将AB分为3∶4的两段，若PQ＝2 cm，则AB的长为(　C　)‎ A．80 cm B．75 cm C．70 cm D．60 cm ‎9．★如图，∠AOB＝∠COD，若∠AOD＝110°，∠BOC＝70°，则以下结论中正确的有①∠AOC＝∠BOD＝90°；②∠AOB＝20°；③∠AOB＝∠AOD－∠AOC；④∠AOB＝∠BOD.(　C　)‎ A．1个 B．2个 C．3个 D．4个 ‎10．射线OA上有B，C两点，若OB＝8，BC＝2，线段OB，BC的中点分别为D，E，则线段DE的长为(　D　)‎ A．5 B．3 C．1 D．5或3‎ 第Ⅱ卷　(非选择题　共90分)‎ 二、填空题(每小题3分，共24分)‎ ‎11．一个角的补角是36°35′，这个角是 143°25′ ．‎ 6‎ ‎12．C，D是直线AB上两点，D是AC的中点，且BC＝AC，DC＝3 cm，则AB＝ 4或8 cm.‎ ‎13．如图，O为直线AB上一点，已知∠1＝40°，OD平分∠BOC，则∠AOD＝ 110° ．‎ ‎ ‎ 第13题图　 　第14题图 ‎14．如图，点A，O，B在同一条直线上，射线OD平分∠BOC，射线OE在∠AOC的内部，且∠DOE＝90°，写出图中所有互为余角的角： ∠1与∠3，∠1与∠4，∠2与∠3，∠2与∠4 .‎ ‎15．如图，一个正三棱柱的底面边长为3 cm，侧棱长为5 cm，则此三棱柱共有 3 个侧面，侧面展开图的面积为 45 cm2.‎ ‎16．★有两根木条，一根长60 cm，另一根长100 cm，将它们的一端重合，放在同一条直线上，则两根木条的中点间的距离是 80cm或20cm ．‎ ‎17．★如图①所示的纸片是∠AOB的一部分，OC平分∠AOB，如图②，把∠AOB沿OC对折成∠COB(OA与OB重合)，从O点引一条射线OE，使∠BOE＝∠EOC，再沿OE把角剪开，若剪开后得到的3个角中最大的一个角为80°，则∠AOB＝ 120 °.‎ ‎18．★如图，下列几何体是由棱长均为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色(底面不涂色)，则第n个几何体中只有两个面涂色的小立方体共有 (8n－4) 个．‎ 选择、填空题答题卡 一、选择题(每小题3分，共30分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 得分 答案 D B A B D D A C C D 二、填空题(每小题3分，共24分)得分：________‎ ‎11. 143°25′ 　　12. 4或8　　13. 110° ‎ ‎14. ∠1与∠3，∠1与∠4，∠2与∠3，∠2与∠4 15． 3 45 ‎ 6‎ ‎16. 80cm或20cm 17． 120　　　 18. (8n－4) ‎ 三、解答题(共66分)‎ ‎19．(8分)计算：‎ ‎(1)48°39′＋67°31′－21°17′；‎ 解：原式＝116°10′－21°17′‎ ‎＝94°53′.‎ ‎(2)23°53′×3－107°43′÷5.‎ 解：原式＝71°39′－21°32′36″‎ ‎＝50°6′24″.‎ ‎20．(9分)如图，已知A，B，O三点．根据下列要求画图：‎ ‎(1)连接线段AB；‎ ‎(2)画射线OA、射线OB；‎ ‎(3)在线段AB上取一点C，在射线OA上取一点D(点C，D不与点A重合)，画直线CD，使直线CD与射线OB交于点E.‎ ‎ ‎ 题图　 　答图 解：如图．‎ ‎21．(8分)如图，已知∠AOE是平角，∠DOE＝20°，OB平分∠AOC，且∠COD ∶∠BOC＝2∶3，求∠BOC的度数．‎ 解：设∠COD＝2x°，则∠BOC＝3x°.‎ ‎∵OB平分∠AOC，‎ ‎∴∠AOB＝3x°.‎ ‎∴2x＋3x＋3x＋20＝180.‎ 解得x＝20.‎ ‎∴∠BOC＝3×20°＝60°.‎ ‎22．(10分)李老师到市场买菜，发现如果把10千克的菜放到托盘秤上，指标盘上的指针转了180度．第二天李老师就给同学们出了两个问题．‎ ‎(1)如果把0.6千克的菜放到托盘秤上，指针转过多少度角？‎ ‎(2)如果指针转了7°12′，这些菜有多少千克？‎ 解：(1)由题意得(180÷10) ×0.6＝10.8(度)．‎ 即指针转过10.8度角．‎ ‎(2)(10÷180)×7°12′＝0.4(千克)．‎ 故这些菜有0.4千克．‎ 6‎ ‎23．(10分)画图并计算：如图，已知线段AB＝2 cm，延长线段AB至点C，使得BC＝AB，再反向延长AC至点D，使得AD＝AC.‎ ‎(1)准确地画出图形，并标出相应的字母；‎ ‎(2)线段DC的中点是哪个点？线段AB的长是线段DC长的几分之几？‎ ‎(3)求出线段BD的长度．‎ 解：(1)画图如图所示．‎ ‎ .‎ ‎(2)线段DC的中点是点A，线段AB的长是线段DC长的.‎ ‎(3)∵BC＝AB＝×2＝1(cm)．‎ ‎∴AC＝AB＋BC＝2＋1＝3(cm)．‎ ‎∵AD＝AC＝3 cm，‎ ‎∴BD＝DA＋AB＝3＋2＝5(cm)．‎ ‎24.(9分)已知m，n满足算式(m－6)2＋＝0.‎ ‎(1)求m，n的值；‎ ‎(2)已知线段AB＝m，在直线AB上取一点P，恰好使AP＝nPB，点Q为PB的中点，求线段AQ的长．‎ 解：(1)m＝6，n＝2.‎ ‎(2)线段AB＝6，AP＝2PB，‎ ‎①当点P在线段AB上时，如图①，‎ ‎∵PA＋PB＝AB，而AB＝6，AP＝2PB，‎ ‎∴2PB＋PB＝6，‎ ‎∴PB＝2，AP＝4.‎ ‎∵点Q是BP的中点，‎ ‎∴PQ＝PB＝1，‎ ‎∴AQ＝AP＋PQ＝4＋1＝5；‎ ‎②当点P在线段AB的延长线上时，如图②，‎ ‎∵PA＝PB＋AB，AB＝6，AP＝2PB，‎ ‎∴6＋PB＝2PB，PB＝6，‎ ‎∵点Q为BP的中点，‎ ‎∴BQ＝PB＝3，‎ ‎∴AQ＝AB＋BQ＝6＋3＝9，‎ ‎∴线段AQ的长为5或9.‎ 6‎ ‎25．(12分)如图①，点O为直线AB上一点，将直角三角板OMN的直角顶点放在点O处，射线OC平分∠MOB.‎ ‎ ‎ ‎① 　②‎ ‎(1)若∠AOM＝30°，求∠CON的度数；‎ ‎(2)若∠AOM＝α，直接写出∠CON的度数(用含α的代数式表示)；‎ ‎(3)将图①中的直角三角板OMN绕顶点O顺时针旋转至图②的位置，一边OM在射线OB的上方，另一边ON在直线AB的下方．‎ ‎①探究∠AOM和∠CON的度数之间的关系，写出你的结论，并说明理由；‎ ‎②当∠AOC＝3∠BON时，求∠AOM的度数．‎ 解：(1)∵∠AOM＝30°，‎ ‎∴∠BOM＝180°－∠AOM＝150°.‎ ‎∵∠MON＝90°，OC平分∠BOM，‎ ‎∴∠CON＝∠MON－∠BOM＝15°.‎ ‎(2)∵∠AOM＝α，‎ ‎∴∠BOM＝180°－∠AOM＝180°－α.‎ ‎∵∠MON＝90°，OC平分∠BOM，‎ ‎∴∠CON＝∠MON－∠BOM＝α.‎ 故∠CON＝α.‎ ‎(3)设∠AOM＝β，则∠BOM＝180°－β，‎ ‎①∠AOM＝2∠CON，‎ 理由：∵OC平分∠BOM，‎ ‎∴∠MOC＝∠BOM＝(180°－β)＝90°－β.‎ ‎∵∠MON＝90°，‎ ‎∴∠CON＝∠MON－∠MOC＝β，‎ ‎∴∠AOM＝2∠CON；‎ ‎②由①知∠BON＝∠MON－∠BOM ‎＝β－90°，‎ ‎∠AOC＝∠AOM＋∠MOC ‎＝90°＋β，‎ ‎∵∠AOC＝3∠BON，∴90°＋β＝3(β－90°)，‎ 解得β＝144°，∴∠AOM＝144°.‎ 6‎