- 1.37 MB
- 2021-04-14 发布
山西省阳泉市2019—2020学年度第一学期期末考试试题
高三理科数学
第Ⅰ卷(选择题共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则的值是
A. B. C. D.
2.若复数满足,则的值是
A. B. C. D.
3.若方程有两个不等的实根和,则的取值范围是
A. B. C. D.
4.随着社会发展对环保的要求,越来越多的燃油汽车被电动汽车取代,为了了解某品牌的电动汽车的节能情况,对某一辆电动汽车“行车数据”的两次记录如下表:
记录时间
累计里程
(单位:公里)
平均耗电量(单位:公里)
剩余续航里程
(单位:公里)
2020年1月1日
5000
0.125
380
2020年1月2日
5100
0.126
246
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,)
下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
A. 等于 B.到之间 C.等于 D.大于
5.已知函数的图象向右平移个单位长度后与原图象重合,则的最小值是
A. B. C. D.
6.宋元时期数学名著《算学启蒙》中有关“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于该思想的一个程序框图,若输入的分别为,则输出的的值是
A. B. C. D.
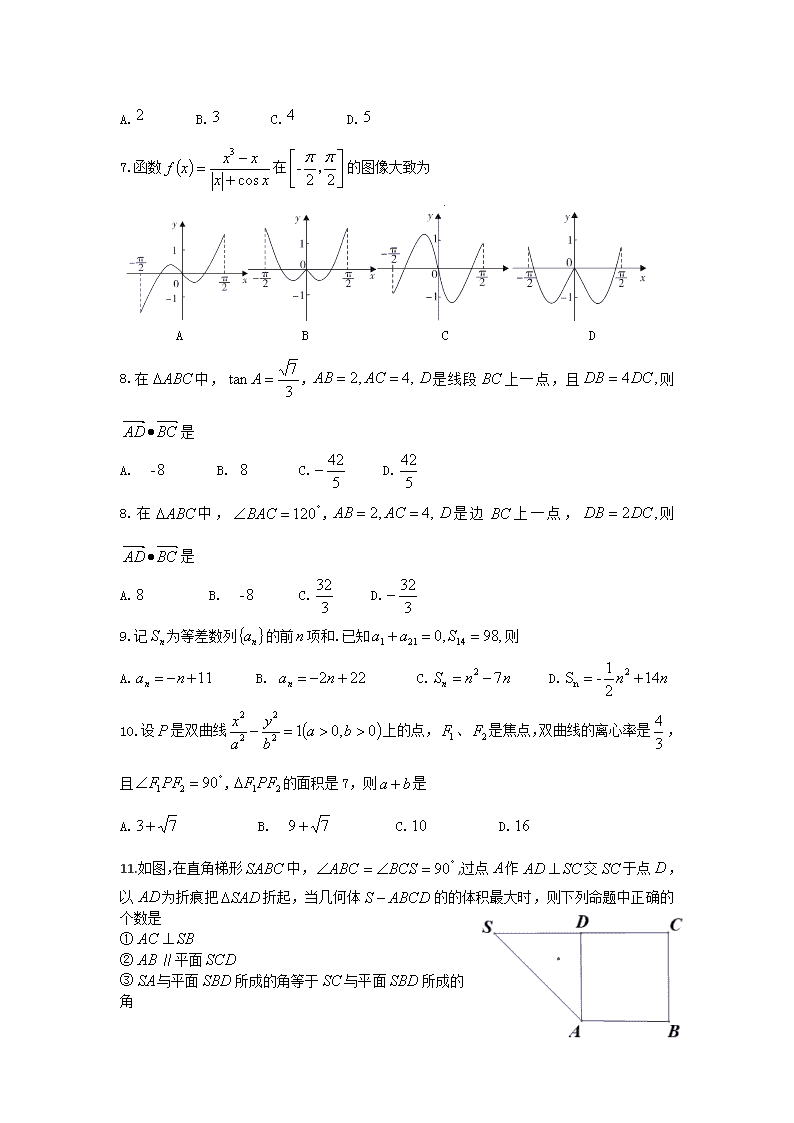
7.函数在的图像大致为
A B C D
8.在中,,是线段上一点,且则是
A. B. C. D.
8.在中,,是边上一点,则是
A. B. C. D.
9.记为等差数列的前项和.已知则
A. B. C. D.
10.设是双曲线上的点,、是焦点,双曲线的离心率是,且,的面积是7,则是
A. B. C. D.
11.如图,在直角梯形中,,过点作交于点,以为折痕把折起,当几何体的的体积最大时,则下列命题中正确的个数是
①
②∥平面
③与平面所成的角等于与平面所成的角
④与所成的角等于与所成的角
A. B. C. D.
12.已知,若不等式在上有解,则实数的取值范围是
A. B.
C. D.
第II卷(非选择题共90分)
本试卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.
二、填空题(本大题共4小题,每小题5分,共20分.)
13.已知曲线在点处的切线与直线垂直,则_____.
14.若展开式中的系数为30,则________.
15.已知是抛物线的焦点,是上一点,的延长线交轴于点.若,则_______________.
16.已知数列满足,数列的前项和,则数列的前n项和___________.
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)在中,角的对边分别为,且.
(1)求;
(2)若,且边上的中线长为,求的面积.
18.(本小题满分12分)如图,在四棱锥中,底面为矩形,,侧面为等边三角形且垂直于底面, 是的中点.
(1)在棱上取一点使直线∥平面并证明;
(2)在(1)的条件下,当棱上存在一点,使得直线与底面所成角为 时,求二面角的余弦值.
19.(本小题满分12分)已知椭圆的两个焦点分别是,离心率,为椭圆上任意一点,且的面积最大值为.
(1) 求椭圆的方程.
(2) 过焦点的直线与圆相切于点,交椭圆于两点,证明:.
20.(本小题满分12分)某市创卫办为了了解该市开展创卫活动的成效,对市民进行了一次创卫满意程度测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”计5分,“不合格”计0分,现随机抽取部分市民的回答问卷,统计结果及对应的频率分布直方图如图所示:
等级
不合格
合格
得分
频数
6
24
(1) 求的值;
(2) 按照分层抽样的方法,从评定等级为“合格”和“不合格”的问卷中随机抽取10份进行问题跟踪调研,现再从这10份问卷中任选4份,记所选4份问卷的量化总分为,求
的分布列及数学期望.
(1) 某评估机构以指标来评估该市创卫活动的成效.若,则认定创卫活动是有效的;否则认为创卫活动无效,应该调整创卫活动方案.在(2)的条件下,判断该市是否应该调整创卫活动方案?
21.(本小题满分12分)已知函数.
(1)讨论的单调性;
(2)设,若且有两个零点,求的取值范围.
请考生在第22,23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.满分10分.
选修4-4:坐标系与参数方程
22.(本小题满分10分)在平面直角坐标系中,曲线的参数方程为(为参数),以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线的普通方程和的平面直角坐标方程;
(2)已知曲线的极坐标方程为,点是曲线与的交点,点是曲线与的交点,,均异于原点,且,求的值.
23.(本小题满分10分)已知的最小值为t.
(1)求t的值;(2)若实数a,b满足,求的最小值.
山西省阳泉市2019—2020学年度第一学期期末考试
高三理科数学参考答案与评分标准
一. 选择题:本大题共12小题,每小题5分,
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
C
D
B
C
A
D
B
A
D
A
二.填空题:本大题共4小题,每小题5分,共20分,
13.e14. 1 15.6 16.
三、解答题(本大题共6小题,共70分,)
17.(1)由已知可得,
所以………………………………………………………………1
在中,……………………………………………………………2
所以.
因为在中,,…………………………………………………………………3
所以,…………………………………………………………………………………4
因为,…………………………………………………………………………………5
所以.………………………………………………………………………………………6
(2)由(1)得,又边上的中线长为,所以,……………7
所以,即,
所以,①……………………………………………………………………8
由余弦定理得,所以,②……………………9
由①②得:,………………………………………………………………………10
所以.……………………………………………………………12
18.(1)在上取中点,在上取中点,连接,由于平行且等于,平行且等于,所以平行且等于,
所以四边形是平行四边形,
所以∥.……………2
直线,
,…………………………………………3
所以∥平面.…………………………………………………………………………4
(2)取中点,连接,由于为正三角形
∴
又∵平面平面,平面平面
∴平面,连接,四边形为正方形。
∵平面,∴平面平面
而平面平面
过作,垂足为,∴平面
∴为与平面所成角,…………………………………6
∴
在中,,∴,
设,,,
∴,∴
在中,,∴
∴,,…………………………………………8
以为坐标原点,、、分别为、、轴建立空间直角坐标系,,,,
,…………………………………………………9
设平面的法向量为,∴
∴法向量可取,………………………………………………………………10
而平面的法向量为……………………………………………………11
设二面角的平面角为
∴.………………………………………………12
19.(1)由椭圆性质知,,…………………………………………………………1
,…………………………………………………………………………………2
解得………………………………………………………………………………3
所以椭圆的方程为.………………………………………………………………4
(2)证明:由(1)可得的斜率存在,故的方程可设为.
因为直线与圆相切,
所以圆心到的距离,解得.………………6
当时,直线的方程为
由联立,可得,显然,
设,则.所以…………………………8
设,由可得,又,
所以.由此可得线段中点重合,故.………………10
同理当时也有.…………………………………………………………11
综上.………………………………………………………………………………12
20.(1)由频率分布直方图可知,得分在的频率为,
故抽取的市民答卷数为:,
又由频率分布直方图可知,得分在的频率为,
所以,…………………………………………………………………………1
又,所以.……………………………………………………………2
.……………………………………………………………………………3
(2)“不合格”和“合格”的人数比例为,因此抽取的人中“不合格”有人,“合格”有人.
所以有共种可能的取值.
的分布列为
20
15
10
5
0
,,,
,.
所以.……………………………9
(3)由(2)可得
……………………………………10
所以,…………………………………………………………11
故我们认为该市的创卫活动是有效的,不需要调整创卫活动方案.…………………………12
21.(1)的定义域为,,
,……………………………………………………………1
对于,,
当时,,则在上是增函数.………………………2
当时,对于,有,则在上是增函数.………3
当时,令,得或,
令,得,
所以在,上是增函数,
在上是减函数.………………………………………4
综上,当时,在上是增函数;
当时,在,上是增函数,
在上是减函数.
(2)由已知可得,因为,所以,而,所以,所以,所以在上单调递增.
所以.………………………………………………………………………6
故在内有两个零点.………………………………………………7
令,定义域为,,
当时,恒成立,在上单调递增,则至多有一个零点,不合题意.……………………………………………………………………………………8
当时,令得,若,则,在上单调递增;若,则,在上单调递减,…………………9
所以,时,
取得极大值,也是最大值,为.…………10
时,,
若有两个零点,则,解得.
所以的取值范围是.……………………………………………………………12
另解:有两根,显然不是方程的根,
因此原方程可化为,
设,,由解得,
由解得,
故在上单调递减,在上单调递增.
所以,所以,所以.
22.【解析】(1)由消去参数,得的普通方程为.
由,得,又,,
所以的直角坐标方程为..……………..5分
(2)由(1)知曲线的普通方程为,所以其极坐标方程为.
设点,的极坐标分别为,,则,,
所以,
所以,即,解得,
又,所以..……………..10分
23.【解析】(1),
∴f(x)在(﹣∞,﹣1)上单调递减,在(﹣1,+∞)上单调递增,
∴f(x)min=f(﹣1)=2,∴t=2;.……………..5分
(2)由(1)可知2a2+2b2=2,则a2+b2=1,
∴,
当且仅当,即,时取等号,
故的最小值为9..……………..10分