九年级上册青岛版数学课件3-3圆周角（3） 10页

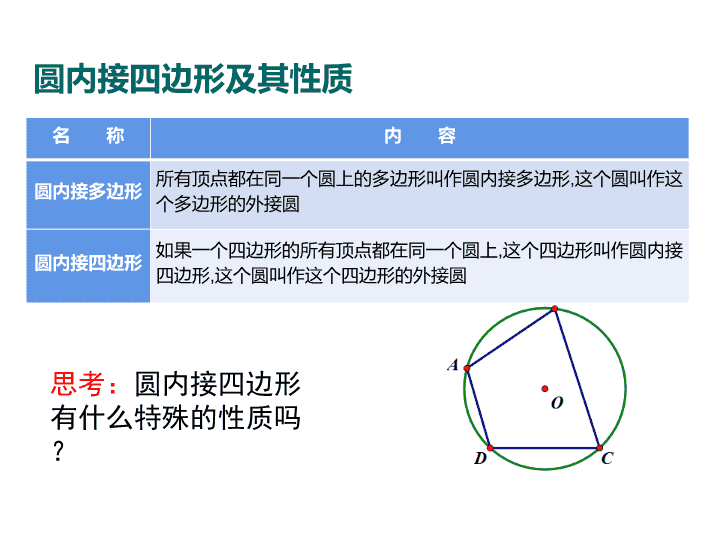
3.3圆周角（3） 学习目标 理解并掌握圆内接四边形的概念及性质并学会运用. (重点) 圆内接四边形及其性质 思考：圆内接四边形 有什么特殊的性质吗？ 名　　称 内　　容 圆内接多边形 所有顶点都在同一个圆上的多边形叫作圆内接多边形,这个圆叫作这 个多边形的外接圆 圆内接四边形 如果一个四边形的所有顶点都在同一个圆上,这个四边形叫作圆内接 四边形,这个圆叫作这个四边形的外接圆 如图，四边形ABCD为☉O的内接四边形，☉O为四 边形ABCD的外接圆. (2)当ABCD为一般四边形时， 猜想：∠A与∠C, ∠B与∠D之间的关系 为 . ∠A+∠C=180º，∠B+∠D=180º (1)当ABCD为矩形时，∠A与∠C, ∠B与∠D之间的 关系为 . ∠A+∠C=180º，∠B+∠D=180º 性质探究 证明：圆内接四边形的对角互补. 已知，如图，四边形ABCD为☉O的内接四边形，☉O为 四边形ABCD的外接圆. 求证∠BAD+∠BCD=180°. 证明：连接OB，OD. 根据圆周角定理，可知 1 21= 12A∠ ∠ ， 1= 2.2C∠ ∠ 1 1= 1 2 = = .2 2A C     （∠ ∠ ） 360 180 由四边形内角和定理可知，∠ABC+∠ADC=180°. 试一试 圆内接四边形的对角互补. 推论4 要点归纳 C O D B A ∵∠A＋∠DCB＝180°， E ∠DCB＋∠DCE＝180°. ∴∠A＝∠DCE. 如图，∠DCE是圆内接四边形ABCD的一个外角，∠A 与∠DCE的大小有何关系？ 想一想 1．四边形ABCD是⊙ O的内接四边形，且∠A=110°， ∠B=80°，则∠C= ，∠D= . 2．⊙ O的内接四边形ABCD中， ∠A∶ ∠B∶ ∠C=1∶ 2∶ 3 ，则∠D= . 70º 100º 90º 练一练 3. 如图，在⊙ O的内接四边形ABCD中，∠BOD＝ 120°，那么∠BCD是(　　) A．120° B．100° C．80° D．60° 解析：∵∠BOD＝120°，∴∠A＝60°， ∴∠C＝180°－60°＝120°，故选A. A 圆周角 定理 推 论 4 圆内接四边形的对角互补. 课堂小结