2018-2019学年福建省东山县第二中学高二上学期期中考试数学（理）试题 Word版 8页

东山二中2018-2019学年高二（上）期中考数学（理科）试卷 一、选择题：本大题共小题，每小题分。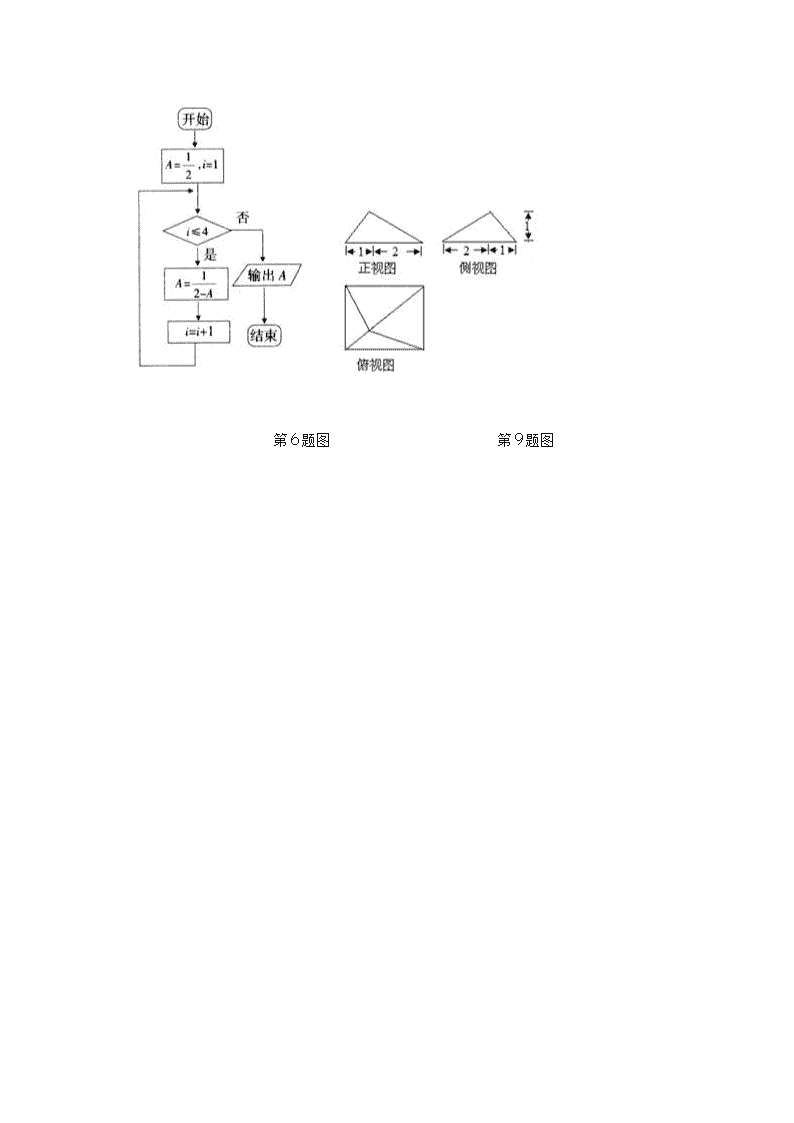‎ ‎１、命题“对任意，都有”的否定为（　　　）‎ Ａ、对任意，使得　　　　Ｂ、不存在，使得 Ｃ、存在，使得　　　　Ｄ、存在，使得 ‎２、袋内有红、白、黑球各个，从中任取两个，则互斥而不对立的事件是（ ）‎ Ａ、至少有一个白球；都是白球　　　　Ｂ、至少有一个白球；红，黑球各一个 Ｃ、至少有一个白球；至少有一个红球　Ｄ、恰有一个白球；一个白球一个黑球 ‎３、某学校有老师，男学生人，女学生人，现用分层抽样的方法从全体师生中抽取一个容量为的样本，已知女学生一共抽取了人，则的值为（　　　）‎ ‎　　Ａ、　　 　　Ｂ、　　　 　 Ｃ、　　　 　　Ｄ、‎ ‎４、命题点在直线上，命题点在曲线上，则使“”为真命题的一个点是（　　　）‎ ‎　　Ａ、　　　 Ｂ、 Ｃ、 Ｄ、‎ ‎５、若样本平均数是，方差是，则另一样本　的平均数和方差分别为（　　　）‎ ‎　　Ａ、　　　　 Ｂ、 Ｃ、 Ｄ、‎ ‎６、执行如图所示的程序框图，则输出的值为（ ）‎ ‎ Ａ、　　　 Ｂ、 Ｃ、 Ｄ、‎ ‎７、设集合，，则（　　　）‎ ‎　　Ａ、 　　　　 Ｂ、‎ ‎　　Ｃ、 　　　 　Ｄ、‎ ‎８、“”是“函数在上单调递增的”（　　　）‎ Ａ、充分不必要条件　　　　　　　　　Ｂ、必要不充分条件 Ｃ、充要条件　　　　　　　　　　　　Ｄ、既不充分也不必要条件 ‎９、某四棱锥的三视图如图所示，则该四棱锥的体积为（　　　）‎ ‎　　Ａ、 　 Ｂ、　 　Ｃ、 Ｄ、‎ ‎10、已知不等式的解集为，则为（　　　）‎ ‎　　Ａ、　　　　　Ｂ、　　　　 Ｃ、　　　　　 Ｄ、‎ ‎11、函数在定义域上的值域为，则的取值范围是（ ）‎ ‎　　Ａ、　　　 Ｂ、 　 Ｃ、 　 　Ｄ、‎ ‎12、已知函数是定义域为的偶函数，当时，，则不等式的解集为（ ）‎ ‎　　Ａ、　　　 Ｂ、 Ｃ、　　　 Ｄ、‎ 二、填空题：本大题共小题，每小题分。‎ ‎13、用“辗转相除法”求得和的最大公约数是 　　　。‎ ‎14、设全集，函数的定义域为集合，函数的定义域为集合，则　　　　　。‎ ‎15、已知命题“”是假命题，则实数的取值范围是　　　　　　。‎ ‎16、若函数是上的减函数，且，设，。若“”是“”的充分不必要条件，则实数的取值范围是　　　　　　。‎ ‎ ‎ ‎ 第６题图　　　　　　　　　　　　第９题图 三、解答题：解答应写出文字说明、证明过程或演算步骤。‎ ‎17、（本小题满分分）‎ 一个袋中装有形状大小完全相同的四个球，球的编号分别为。‎ ‎⑴、从袋中随机取两个球，求取出的球的编号之和不大于的概率；(分)‎ ‎⑵、先从袋中随机取一球，该球的编号为，将球放回袋中，然后再从袋中随机取一个球，该球的编号为，求的概率。(分)‎ ‎18、（本小题满分分）‎ 命题：实数满足（），命题：实数满足。‎ ‎⑴、若，且为真，求实数的取值范围；(分)‎ ‎⑵、若是的充分不必要条件，求实数的取值范围。(分)‎ ‎19、（本小题满分分）‎ 已知方程有两个不相等的负根；方程无实根。若为真，为假，求实数的取值范围。‎ ‎20、（本小题满分分）‎ 如图，已知为圆的直径，，点为线段上一点，且，点为圆上一点，，点在圆所在平面上的正投影为点，⑴、求证：平面；⑵、求直线与平面所成的角。‎ ‎21、（本小题满分分）‎ 已知圆的圆心在直线上，且经过点，。‎ ‎⑴、求圆的标准方程；‎ ‎⑵、直线过点且与圆相交的弦长为，求直线的方程。‎ ‎22、（本小题满分分）‎ 已知函数是定义在上的奇函数，且对任意实数，恒有。当时，。‎ ‎⑴、当时，求的解析式。⑵、计算：。‎ 东山二中高二（上）理科数学期中考参考答案 一、选择题：本大题共小题，每小题分。‎ ‎１、；２、；３、；４、；５、；６、；‎ ‎７、；８、；９、；10、；11、；12、；‎ 二、填空题：本大题共小题，每小题分。‎ ‎13、；14、；15、；16、；‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤。‎ ‎17、（本小题满分分）‎ 解：⑴从袋中随机取两个球，所有可能的的基本事件有：‎ 和，和，和，和，和，和，共个。‎ 从袋中取出的球的编号之和不大于的事件共有和，和两个，‎ 故所求事件的概率为。‎ ‎⑵用表示基本事件有：，，，，，，，，‎ ‎ ，，，，，，，，共个。‎ ‎ 满足有，，，共个，‎ ‎ 满足的基本事件共个，‎ ‎ 故满足的概率为。‎ ‎18、（本小题满分分）‎ 解：⑴、命题为真时，；命题为真时，；‎ ‎ 故为真时，实数的取值范围为。‎ ‎⑵、由已知得命题：，命题：，‎ 是的充分不必要条件，是的充分不必要条件，‎ ‎，解得：，‎ 故实数的取值范围为。‎ ‎19、（本小题满分分）‎ 解：若方程有两个不相等的负根，则，‎ ‎　　　解得：，即；‎ 若方程无实根，则，‎ ‎　解得：，即。‎ 为真，为假，命题为一真一假，即真假或假真。‎ 若真假，则，得；‎ 若假真，则，得；‎ 综上得：实数的取值范围为。‎ ‎20、（本小题满分分）‎ 解：⑴、连接，由，得点为的中点，‎ 为圆的直径，，又，‎ ‎，为等边三角形，；‎ 点在圆所在平面上的正投影为点，‎ 平面，又平面，‎ ‎，又，‎ 故平面。‎ ‎⑵、由⑴得：是直线与平面所成的角，‎ 是边长为的等边三角形，‎ ‎，又，‎ ‎，，‎ 故直线与平面所成的角为。‎ ‎21、（本小题满分分）‎ 解：⑴、由已知得：圆心在线段的中垂线上，其方程为，‎ 由，得圆心，从而半径为，‎ 故圆的标准方程为。‎ ‎⑵、当直线的斜率不存在时，直线方程为，‎ ‎ 圆心直线的距离为，又，‎ ‎ 直线被圆截得的弦长为，符合题意；‎ 当直线的斜率存在时，设直线方程为，即，‎ ‎ 圆心直线的距离为，又，‎ ‎ ，，解得：，‎ ‎ 直线方程为，‎ 故所求直线方程为或。‎ ‎22、（本小题满分分）‎ 解：⑴、，，‎ 是最小正周期为的周期函数，‎ 设，则，，‎ 函数是定义在上的奇函数，，‎ ‎，，‎ 当时，，，‎ 是最小正周期为的周期函数，‎ 故当时，。‎ ‎⑵、由⑴可得：，，，，‎ ‎，‎ 又是最小正周期为的周期函数，‎ ‎，‎ 故。‎