2016年高考数学（文科）真题分类汇编F单元　平面向量 5页

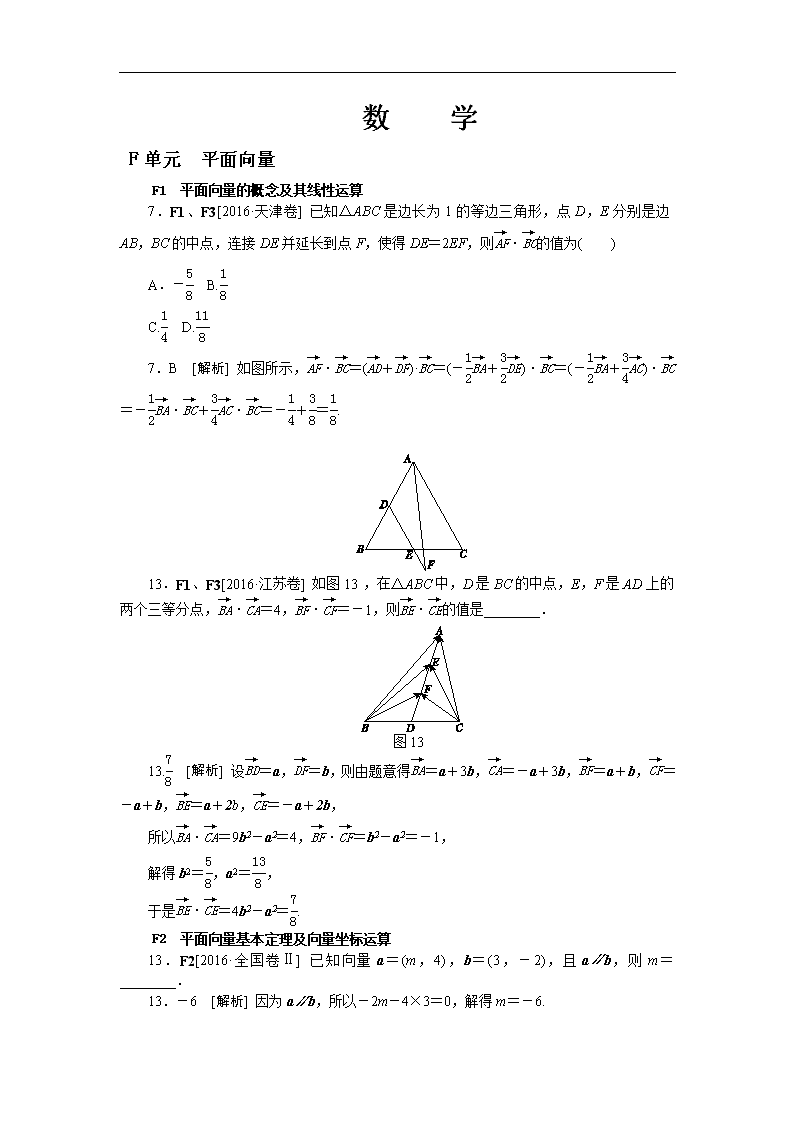
‎ 数 学 ‎ F单元　平面向量 ‎ F1　平面向量的概念及其线性运算 ‎7．F1、F3[2016·天津卷] 已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE＝2EF，则·的值为(　　)‎ A．－ B. C. D. ‎7．B　[解析] 如图所示，·＝(＋)·＝(－＋)·＝(－＋)·＝－·＋·＝－＋＝.‎ ‎13．F1、F3[2016·江苏卷] 如图13，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，·＝4，·＝－1，则·的值是________．‎ 图13‎ ‎13.　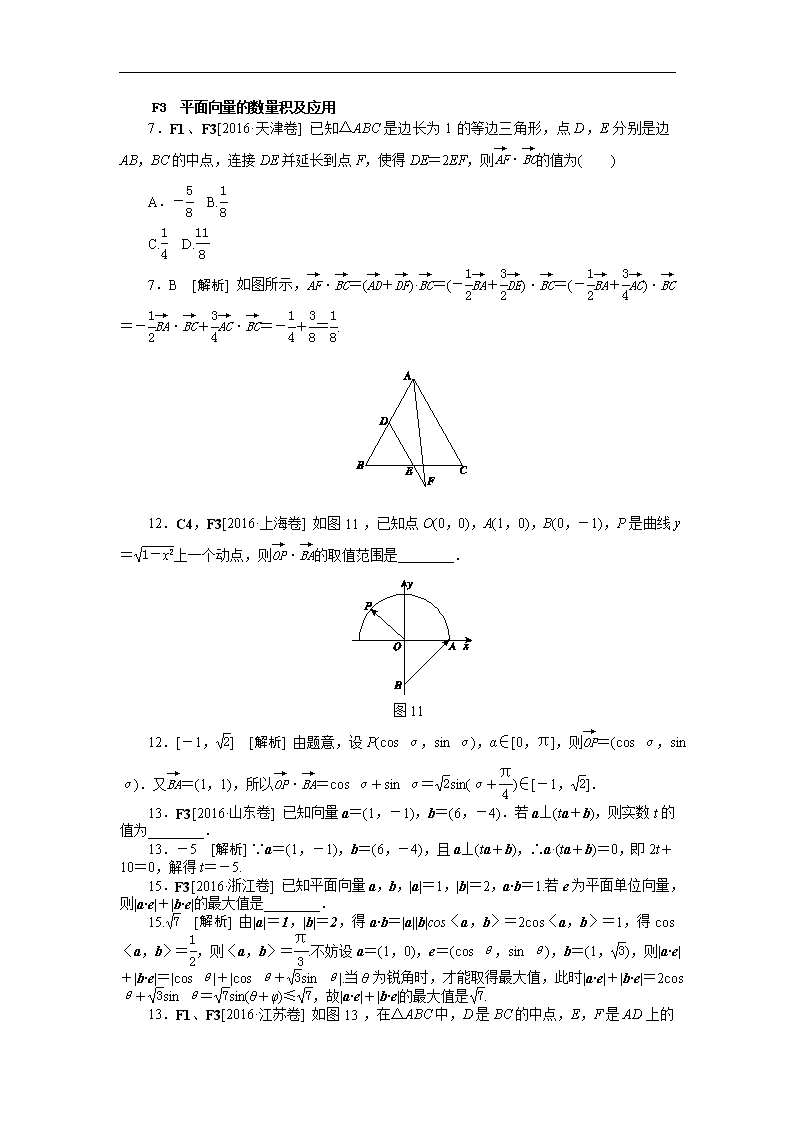[解析] 设＝a，＝b，则由题意得＝a＋3b，＝－a＋3b，＝a＋b，＝－a＋b，＝a＋2b，＝－a＋2b，‎ 所以·＝9b2－a2＝4，·＝b2－a2＝－1，‎ 解得b2＝，a2＝，‎ 于是·＝4b2－a2＝.‎ F2　平面向量基本定理及向量坐标运算 ‎13．F2[2016·全国卷Ⅱ] 已知向量a＝(m，4)，b＝(3，－2)，且a∥b，则m＝________．‎ ‎13．－6　[解析] 因为a∥b，所以－2m－4×3＝0，解得m＝－6.‎ F3　平面向量的数量积及应用 ‎7．F1、F3[2016·天津卷] 已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE＝2EF，则·的值为(　　)‎ A．－ B. C. D. ‎7．B　[解析] 如图所示，·＝(＋)·＝(－＋)·＝(－＋)·＝－·＋·＝－＋＝.‎ ‎12．C4，F3[2016·上海卷] 如图11，已知点O(0，0)，A(1，0)，B(0，－1)，P是曲线y＝上一个动点，则·的取值范围是________．‎ 图11‎ ‎12．[－1，]　[解析] 由题意，设P(cos α，sin α)，α∈[0，π]，则＝(cos α，sin α)．又＝(1，1)，所以·＝cos α＋sin α＝sin(α＋)∈[－1，]．‎ ‎13．F3[2016·山东卷] 已知向量a＝(1，－1)，b＝(6，－4)．若a⊥(ta＋b)，则实数t的值为________．‎ ‎13．－5　[解析] ∵a＝(1，－1)，b＝(6，－4)，且a⊥(ta＋b)，∴a·(ta＋b)＝0，即2t＋10＝0，解得t＝－5.‎ ‎15．F3[2016·浙江卷] 已知平面向量a，b，|a|＝1，|b|＝2，a·b＝1.若e为平面单位向量，则|a·e|＋|b·e|的最大值是________．‎ ‎15.　[解析] 由|a|＝1，|b|＝2，得a·b＝|a||b|cos〈a，b〉＝2cos〈a，b〉＝1，得cos〈a，b〉＝，则〈a，b〉＝.不妨设a＝(1，0)，e＝(cos θ，sin θ)，b＝(1，)，则|a·e|＋|b·e|＝|cos θ|＋|cos θ＋sin θ|.当θ为锐角时，才能取得最大值，此时|a·e|＋|b·e|＝2cos θ＋sin θ＝sin(θ＋φ)≤，故|a·e|＋|b·e|的最大值是.‎ ‎13．F1、F3[2016·江苏卷] 如图13，在△ABC中，D是BC的中点，E，F是AD 上的两个三等分点，·＝4，·＝－1，则·的值是________．‎ 图13‎ ‎13.　[解析] 设＝a，＝b，则由题意得＝a＋3b，＝－a＋3b，＝a＋b，＝－a＋b，＝a＋2b，＝－a＋2b，‎ 所以·＝9b2－a2＝4，·＝b2－a2＝－1，‎ 解得b2＝，a2＝，‎ 于是·＝4b2－a2＝.‎ ‎9．F3[2016·北京卷] 已知向量a＝(1，)，b＝(，1)，则a与b夹角的大小为________．‎ ‎9.　[解析] 根据题意得|a|＝＝2，|b|＝＝2，a·b＝＋＝2.设a与b的夹角为θ，则cos θ ＝＝＝，因为θ∈[0，π]，所以θ＝.‎ ‎13．F3[2016·全国卷Ⅰ] 设向量a＝(x，x＋1)，b＝(1，2)，且a⊥b，则x＝________．‎ ‎13．－　[解析] 由题意，a·b＝0，即x＋2(x＋1)＝0，∴x＝－.‎ ‎ F4 单元综合 ‎9．F4[2016·四川卷] 已知正三角形ABC的边长为2，平面ABC内的动点P，M满足||＝1，＝，则||2的最大值是(　　)‎ A. B. C. D. ‎9．B　[解析] 方法一：以A为原点建立如图所示的直角坐标系，则B，C两点的坐标分别为(3，－)，(3，)．‎ 由||＝1，设P点的坐标为(cos θ，sin θ)，其中θ∈[0，2π)．‎ 而＝，即M是PC的中点，‎ 所以M点的坐标为，‎ 则||2＝＋＝.‎ 又θ∈[0，2π)，所以当θ－＝，即θ＝π时，||2取得最大值.‎ 方法二：设AC的中点为T，则||＝3.‎ 因为＝，所以M是PC的中点．易知＝(＋)＝(＋＋)＝(2＋)＝＋，‎ 所以||2＝(＋)2＝||2＋||2＋·＝||2＋||2＋||||cos〈，〉≤9＋＋3×1×1＝，‎ 当且仅当〈，〉＝0，即与同向时，等号成立．‎ ‎1. [2016·山东枣庄质检]在平行四边形ABCD中，对角线AC与BD交于点O，＝λ，则实数λ＝(　　)‎ A. － B. C. －2 D. 2‎ ‎1. A　[解析] 根据向量平行四边形法则得＋＝＝2，因为＝λ，所以λ＝－.‎ ‎1. [2016·北京海淀区期末]如图K221所示， 正方形ABCD中，E为DC的中点，若＝λ＋μ，则λ＋μ的值为(　　)‎ 图K221‎ A. B. － C. 1 D. －1‎ ‎1. A　[解析] 因为E为DC的中点，所以＝＋＝‎ ＋＋＝＋＝＋，即＝－＋，又＝λ＋μ，所以μ＝1，λ＝－，故λ＋μ的值为.‎ ‎15. [2016·合肥一检]如图K231所示，已知等边三角形ABC的边长为2，若＝3， ‎＝，则·＝________．‎ 图K231‎ ‎15. －2　[解析] ∵＝，∴D为AC的中点，即＝，‎ ‎∴＝＋.∵＝3，∴＝＋，‎ ‎∴·＝·＝·＋‎ ·＋·＋·＝－4＋×4×cos 60°＋×4×cos 60°＋×4×cos 60°＝－2.‎ ‎ ‎