- 909.00 KB
- 2021-04-14 发布
2017年高考全国统一考试全真模拟试题(二)
数学(文科)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集,集合,集合,则图中阴影部分表示的集合是( )
A. B. C. D.
2.设复数,则的虚部是( )
A. B. C. D.
3.在中,分别在上,且,若,则( )
A. B. C. D.
4.下列命题中正确命题的个数是( )
(1)对于命题,使得,则,均有;
(2)命题“已知,若,则或”是真命题;
(3)回归直线的斜率的估计值为,样本点的中心为,则回归直线方程为;
(4)是直线与直线互相垂直的充要条件.
A. B. C. D.
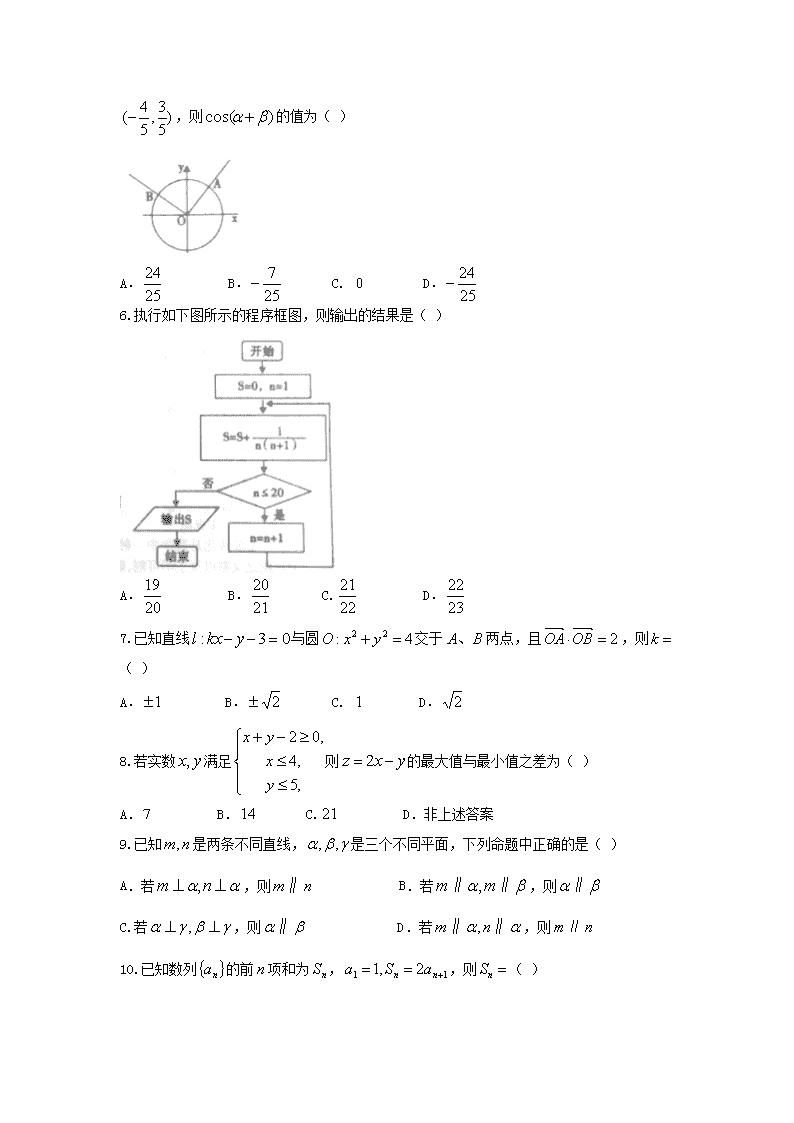
5.如图,在平面直角坐标系中,角的顶点与坐标原点重合,始边与轴的非负半轴重合,它们的终边分别与单位圆相交于两点,若点的坐标分别为和
,则的值为( )
A. B. C. D.
6.执行如下图所示的程序框图,则输出的结果是( )
A. B. C. D.
7.已知直线与圆交于两点,且,则( )
A. B. C. D.
8.若实数满足则的最大值与最小值之差为( )
A. B. C. D.非上述答案
9.已知是两条不同直线,是三个不同平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.已知数列的前项和为,,则( )
A. B. C. D.
11.若曲线的焦点恰好是曲线的右焦点,且与交点的连线过点,则曲线的离心率为( )
A. B. C. D.
12.已知函数满足,且当时,,则( )
A. B.
C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.在平行四边形中,已知,则四边形的面积为 .
14.在等差数列中,,其前项的和为,若,则 .
15.如图为某几何体的三视图,则其体积为 .
16.有限与无限转化是数学中一种重要思想方法,如在《九章算式》方田章源田术(刘徽注)中:“割之又割以至于不可割,则与圆合体而无所失矣.”说明“割圆术”是一种无限与有限的转化过程,再如中“...”即代表无限次重复,但原式却是个定值,这可以通过方程确定出来,类似地可以把循环小数化为分数,把化为分数的结果为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知函数.
(1)求的单调递增区间;
(2)在中,三内角的对边分别为,已知,成等差数列,且,求的值.
18. 某志愿者到山区小学支教,为了解留守儿童的幸福感,该志愿者对某班名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如下(注:图中幸福指数低于,说明孩子幸福感弱;幸福指数不低于,说明孩子幸福感强).
(1)根据茎叶图中的数据完成列联表,并判断能否有的把握认为孩子的幸福感强与是否是留守儿童有关?
幸福感强
幸福感弱
合计
留守儿童
非留守儿童
合计
(2)从个留守儿童中按幸福感强弱进行分层抽样,共抽取人,又在这人中随机抽取人进行家访,求这个学生中恰有一人幸福感强的概率.
参考公式:.
附表:
19.如图,在四棱锥中,底面为直角梯形,且,,平面底面,为的中点,是棱的中点,.
(1)求证:平面;
(2)求三棱锥的体积.
20.已知为椭圆的左右焦点,点为其上一点,且有.
(1)求椭圆的标准方程;
(2)圆是以,为直径的圆,直线与圆相切,并与椭圆交于不同的两点,若,求的值.
21. 已知函数为实数)的图像在点处的切线方程为.
(1)求实数的值及函数的单调区间;
(2)设函数,证明时,.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线(为参数),将上的所有点的横坐标、纵坐标分别伸长为原来的和倍后得到曲线.以平面直角坐标系的原点为极点,轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线.
(1)试写出曲线的极坐标方程与曲线的参数方程;
(2)在曲线上求一点,使点到直线的距离最小,并求此最小值.
23.选修4-5:不等式选讲
已知和是任意非零实数.
(1)求的最小值;
(2)若不等式恒成立,求实数的取值范围.
2017年高考全国统一考试全真模拟试题(二)
数学(文科)参考答案
一、选择题
1-5:AAABA 6-10:CCCDD 11、12:BD
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)
,
由得,,
故的单调递增区间是.
(2),,,
于是,故.
由成等差数列得:,
由得:,
由余弦定理得:,
于是,.
18.解:(1)
幸福感强
幸福感弱
合计
留守儿童
非留守儿童
合计
∴,
∴有的把握认为孩子的幸福感强与是否是留守儿童有关.
(2)按分层抽样的方法可抽出幸福感强的孩子人,记作;幸福感弱的孩子人,记作.
“抽取人”包含的基本事件有共个,
事件:“恰有一人幸福感强”包含的基本事件有个,
∴.
19.解:(1)连接,因为,,所以四边形为平行四边形.
连接交于,连接,则,
又平面,平面,所以平面.
(2),
由于平面底面,底面,
所以是三棱锥的高,且,
由(1)知是三棱锥的高,,
所以,则.
20.解:(1)由题意,椭圆的长轴长,得,
因为点在椭圆上,∴,
所以椭圆的标准方程为.
(2)当直线与圆相切,得,即,
设,
由消去,整理得,
由题意可知圆在椭圆内,所以直线必与椭圆相交,
所以,
,
所以,
因为,所以,
又因为,所以,解得.
21.解:(1)由题得,函数的定义域为,,
因为曲线在点处的切线方程为,
所以解得.
令,得,
当时,,在区间内单调递减;
当时,,在区间内单调递增.
所以函数的单调递减区间为,单调递增区间为.
(2)由(1)得,.
由,得,即.
要证,需证,即证,
设,则要证,等价于证:.
令,则,
∴在区间内单调递增,,
即,故.
22.解:(1)由已知得曲线的直角坐标方程是,
所以曲线的极坐标方程是.
根据已知曲线的参数方程伸缩变换得到曲线的参数方程是(为参数).
(2)设,由已知得直线的直角坐标方程是,
即,所以点到直线的距离
,
当即时,,此时点的坐标是,
所以曲线上的一点到直线的距离最小,最小值是.
23.解:(1)∵对于任意非零实数和恒成立,
当且仅当时取等号,
∴的最小值等于.
(2)∵的最小值,
由(1)可知的最小值等于,
实数的取值范围即为不等式的解,
解不等式得,即的取值范围为.