- 621.00 KB
- 2021-04-14 发布
与抛物线的焦点有关的六个性质的多种证明方法
本文在证明性质中用到了直线方程的三种设法:设斜率法,设斜率倒数法和参数法,有些证明还用到几何法和代数法.
定理及证明
图形
一、 抛物线的焦点弦的点的坐标的性质
若AB是抛物线的焦点弦(过焦点的弦),
且,,则:,.
两种证法比较:
证法一:斜率设法()需要讨论,比较复杂;
证法二:斜率倒数()设法比较简单.
证法一:因为焦点坐标为F(,0),当AB不垂直于x轴时,可设直线AB的方程为: ,显然.
由得: ,(这种设法下,要注意把代入直线,这样消元比较简单,可以叫做以曲代直,即把曲线代入直线)
∴,.
当AB⊥x轴时,直线AB方程为,则,
,∴,同上也有:.
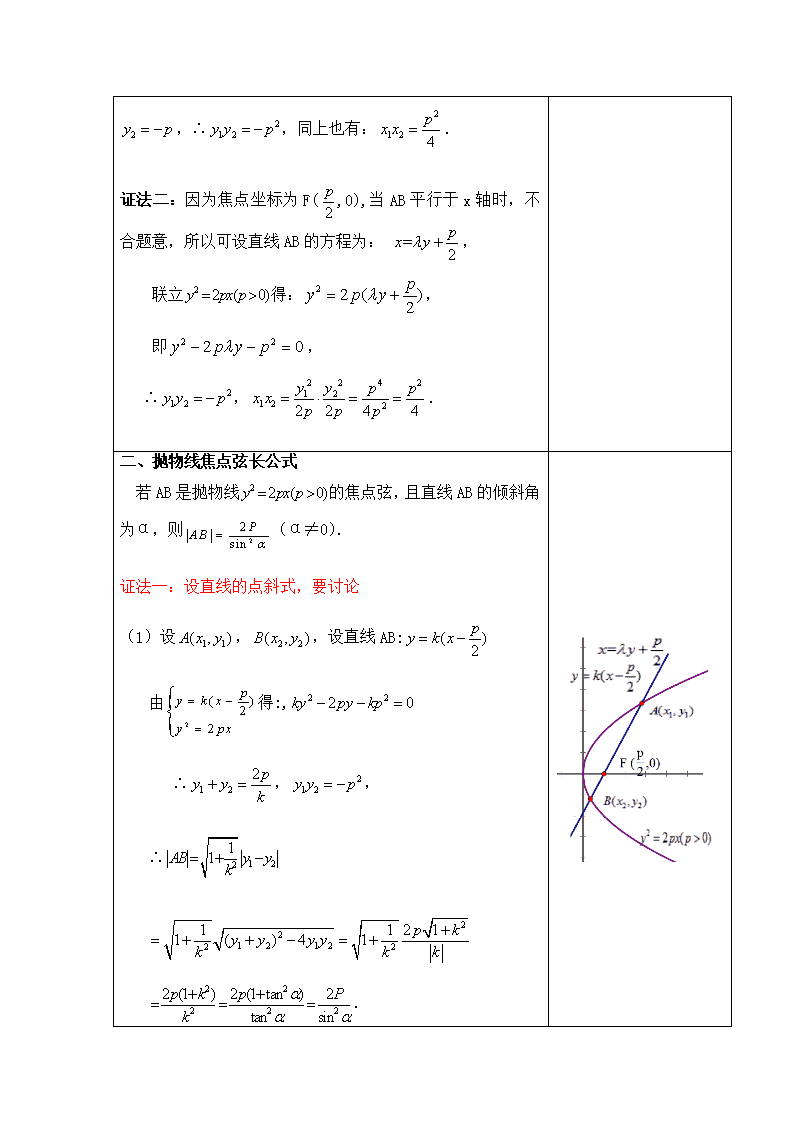
证法二:因为焦点坐标为F(,0),当AB平行于x轴时,不合题意,所以可设直线AB的方程为: ,
联立得:,
即,
∴,.
二、抛物线焦点弦长公式
若AB是抛物线的焦点弦,且直线AB的倾斜角为α,则(α≠0).
证法一:设直线的点斜式,要讨论
(1)设,,设直线AB:
由得:,
∴,,
∴
.
易验证,结论对斜率不存在时也成立.
注意:AB为通径时,,的值最大,最小.
证法二:设直线的参数方程
因为焦点坐标为F(,0),所以可设直线AB的参数方程为: ,
代入,得,
即,
,
所以,
所以.
证法三:利用抛物线的定义,仍然用证法一的设法,没有斜率要单独说明
三、抛物线焦半径长的倒数和是定值
直线AB是过抛物线焦点F,求证:为定值.
证法一:先利用定义
设,,由抛物线的定义知:,,又+=,所以+=,且由结论一知:.
则:
=(常数)
证法二:利用直线参数方程
因为焦点坐标为F(,0),所以可设直线AB的参数方程为: ,
代入,得,
即,
,
所以,
所以
.
本题有几何解释,读者思考(提示:用比例线段)
四、原点处的三点共线
过任作直线交抛物线于,
过分别作准线的垂线,垂足为,
为坐标原点,则三点共线,三点共线.
证法一:(几何法)连结交轴于点,由已知,由抛物线定义于是,所以,即为的中点,即与重合.所以三点共线,
同理可证三点共线.
证法二:(代数法)设直线的方程为 ,
联立得,显然,
设,则,又,
所以所以,
所以三点共线,
同理可证三点共线.
五、点处的角平分线:
过任作直线交抛物线于,
点为定点, 则.
证法一:(几何法) 过分别作准线的垂线,
垂足为, 延长交的延长线于 ,
由及
得:,
所以,又,
所以
又
所以.
证法二:(代数法)设的方程为:,联立得,显然,设,
则,又,所以
,所以,所以的倾斜角互补,所以.
六、点 处的垂线:
过任作直线交抛物线于,
过分别作准线的垂线,垂足为,
则.
证法一:(代数法)设的方程为:,
联立得,
显然,设,
则,
∴
∴.
证法二:(几何法)
由定义,,
∴,
,∴,
∴,
又∵,
∴,
∴,∴,∴