- 471.00 KB
- 2021-04-14 发布
安平中学2017—2018学年第一学期期中考试
数学试题 (高二文)
考试时间 120分钟 试题分数 150分
一、 选择题:(每题只有一个正确选项。共12个小题,每题5分,共60分。)
1.双曲线的虚轴长是( )
A.2 B. C. D.8
2.若函数在区间内可导,且则
的值为( )
A. B. C. D.
3.已知椭圆C:的长轴长、短轴长、焦距成等差数列,则该椭圆的方程是( )
A. B. C. D.
4.,若,则的值等于( )
A. B. C. D.
5.已知斜率为3的直线L与双曲线C: =1(a>0,b>0)交于A,B两点,若点P(6,2)是AB的中点,则双曲线C的离心率等于( )
A. B. C.2 D.
6.曲线在处的切线平行于直线,则点的坐标为( )
A. B. C.和 D.和
7.已知椭圆的左、右焦点分别为F1、F2,过F2的直线交椭圆C于P、Q两点,若|F1P|+|F1Q|=10,则|PQ|等于( )
A.8 B.6 C.4 D.2
8. 若曲线的一条切线与直线垂直,则的方程为( )
A. B. C. D.
9.已知F1、F2是双曲线(a>0,b>0)的左、右焦点,点F1关于渐近线的对称点恰好落在以F2为圆心,|OF2|为半径的圆上,则该双曲线的离心率为( )
A. B. C.2 D.3
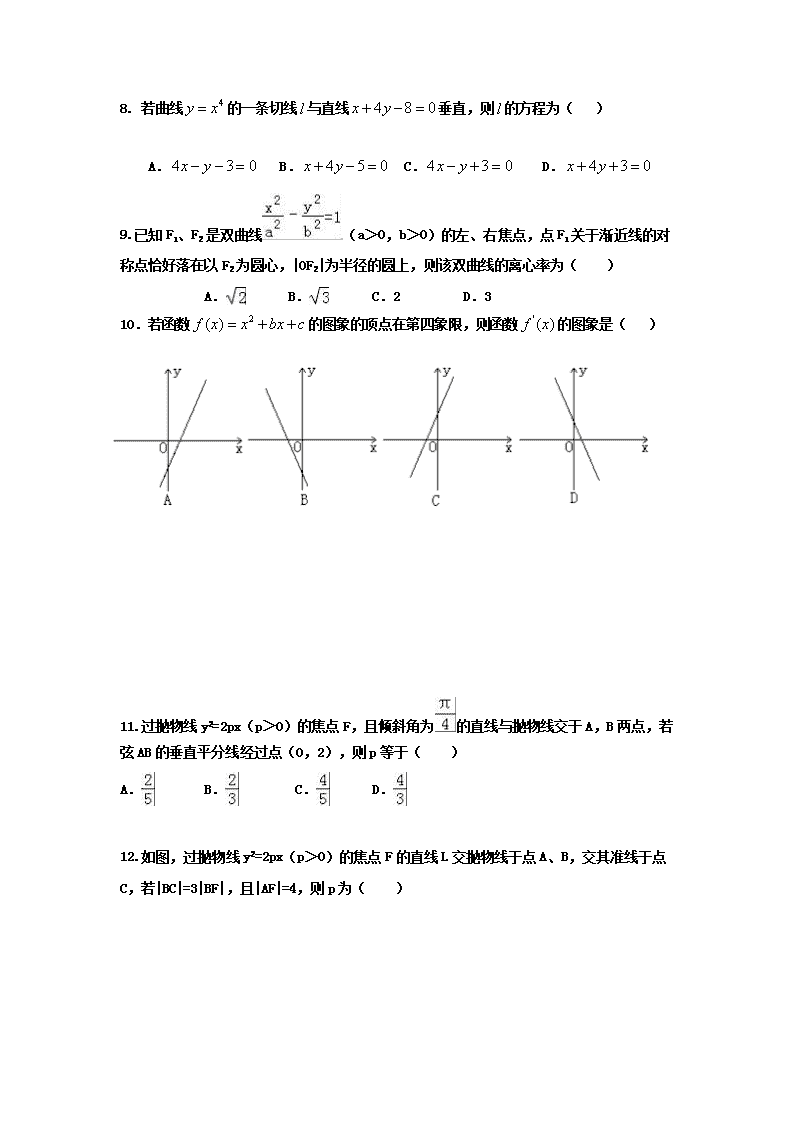
10.若函数的图象的顶点在第四象限,则函数的图象是( )
11.过抛物线y2=2px(p>0)的焦点F,且倾斜角为的直线与抛物线交于A,B两点,若弦AB的垂直平分线经过点(0,2),则p等于( )
A. B. C. D.
12.如图,过抛物线y2=2px(p>0)的焦点F的直线L交抛物线于点A、B,交其准线于点C,若|BC|=3|BF|,且|AF|=4,则p为( )
A. B.2 C. D.
二.填空题(共4个小题,每题5分,共20分。)
13.函数的导数为_________________.
14.已知曲线与在处的切线互相垂直,则的值为______.
15.设椭圆C1的离心率为,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为__________.
16.给出下列结论:
动点M(x,y)分别到两定点(﹣3,0)、(3,0)连线的斜率之乘积为,设M(x,y)的轨迹为曲线C,F1、F2分别为曲线C的左、右焦点,则下列命题中:
(1)曲线C的焦点坐标为F1(﹣5,0)、F2(5,0);
(2)若∠F1MF2=90°,则S=32;
(3)当x<0时,△F1MF2的内切圆圆心在直线x=﹣3上;
(4)设A(6,1),则|MA|+|MF2|的最小值为;
其中正确命题的序号是: .(把你认为正确命题的序号都填上)
三、 解答题:(解答题应写出必要的文字说明和演算步骤)
17.(本小题10分)
已知椭圆C的焦点分别为F1(﹣2,0)和F2(2,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标.
18. (本小题12分)已知抛物线C:y2=2px(p>0)的焦点为F,抛物线上横坐标为的点到抛物线顶点的距离与该点到抛物线准线的距离相等.
(1)求抛物线C的方程;
(2)设直线x﹣my﹣6=0与抛物线C交于A、B两点,若∠AFB=90°,求实数m的值.
19. (本小题12分)
求曲线在点(1,f(1))处的切线方程.
20. (本小题12分)
已知点A(0,﹣2),椭圆E: +=1(a>b>0)的离心率为,F是椭圆的焦点,直线AF的斜率为,O为坐标原点.
(Ⅰ)求E的方程;
(Ⅱ)设过点A的直线L与E相交于P,Q两点,当△OPQ的面积最大时,求L的方程.
21.(本小题12分)(1).求垂直于直线并且与曲线相切的直线方程。
(2). 已知的图象经过点,且在处的切线方程是 ,求的解析式
22. (本小题12分)
已知A(2,0),O为坐标原点,动点P满足|+|+|﹣|=4
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过点A且不垂直于坐标轴的直线L交轨迹C于不同的两点M,N,线段MN的垂直平分线与x轴交于点D,线段MN的中点为H,求的取值范围.
高二文班数学答案
BBCDA CBACA CC
13. 14.
。
15. ﹣=1 16. (1)(3)
17.(本小题10分)解:设椭圆C的方程为+=1,
由题意a=3,c=2,b==1.∴椭圆C的方程为+y2=1.
联立方程组,消y得10x2+36x+27=0,
因为该二次方程的判别式△>0,所以直线与椭圆有两个不同的交点,
设A(x1,y1),B(x2,y2),则x1+x2=﹣,
故线段AB的中点坐标为(﹣,).
18.(本小题12分)解:(1)抛物线上横坐标为的点的坐标为(,±),到抛物线顶点的距离的平方为+p,
∵抛物线上横坐标为的点到抛物线顶点的距离与其到准线的距离相等,
∴+p=(+)2, ∴p=2 抛物线的方程为:y2=4x.
(2)由题意,直线l:x=my+6,代入y2=4x得,y2﹣4my﹣24=0,
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=﹣24,
∵∠AFB=90°,∴FA⊥FB,即•=0
可得:(x1﹣1)(x2﹣1)+y1y2=0 ∴(1+m2)y1y2+5m(y1+y2)+25=0
∴﹣24(1+m2)+20m2+25=0, 解得:m=±.
19.(本小题12分)解:由题意,,
∴,
∴f′(1)=e
∴
∴
∴所求切线方程为y﹣e+=e(x﹣1),即
故答案为:
20.解:(Ⅰ) 设F(c,0),由条件知,得=又,
所以a=2=,b2=a2﹣c2=1,故E的方程.….
(Ⅱ)依题意当l⊥x轴不合题意,故设直线l:y=kx﹣2,设P(x1,y1),Q(x2,y2)
将y=kx﹣2代入,得(1+4k2)x2﹣16kx+12=0,
当△=16(4k2﹣3)>0,即时,
从而=+
又点O到直线PQ的距离,所以△OPQ的面积=,
设,则t>0,,
当且仅当t=2,k=±等号成立,且满足△>0,
所以当△OPQ的面积最大时,l的方程为:y=x﹣2或y=﹣x﹣2.
21.(本小题12分)
(1).解:设切点为,函数的导数为
切线的斜率,得,代入到
得,即,。
(2).解:的图象经过点,则,
切点为,则的图象经过点
得
22.(本小题12分)解:(Ⅰ)设P(x,y),由已知得+=>4,
根据椭圆定义知P点轨迹为以(2,0)和(﹣2,0)为焦点,长轴长为的椭圆,即有a=2,c=2,b=2,则动点P的轨迹C的方程为+=1;
(Ⅱ)设直线L的斜率为k(k≠0),M(x1,y1),N(x2,y2),
则L的方程为y=k(x﹣2),将其代入+=1,
整理得(1+2k2)x2﹣8k2x+8k2﹣8=0,
由于A在椭圆内,当然对任意实数k都有△>0,
根据韦达定理得x1+x2=,x1x2=,
那么|MN|==•
=,
y1+y2=k(x1﹣2)+k(x2﹣2)=k(x1+x2)﹣4k=,
线段MN中点H的坐标为(,),
那么线段MN的垂直平分线方程为y+=﹣(x﹣),
令y=0,得D(,0),
|DH|==,
则=•=•,
由k≠0,可得1+∈(1,+∞),
于是∈(0,).