- 1.91 MB
- 2021-04-14 发布
2019--2020学年度第一学期半期考试试卷高二数学
一、选择题
1.设集合,,则 ( )
A. B.
C. D.
【答案】C
【解析】
【分析】
由已知求得集合S,再求出,从而求出,得选项.
【详解】由得或,所以,所以,
又,所以,
故选:C.
【点睛】本题考查集合的交集和补集运算,属于基础题.
2.=( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据诱导公式,以及特殊角所对应的三角函数值,即可求出结果.
【详解】因为.
故选D
【点睛】本题主要考查三角函数的值,熟记诱导公式即可,属于基础题型.
3.设向量 , 满足, 则 ( )
A. 2 B. C. 3 D.
【答案】B
【解析】
【分析】
根据,代入可求得,从而得.
【详解】由于,所以,
所以,
故选:B.
【点睛】本题考查向量的数量积运算,一般求向量的模时,先求该向量的平方,属于基础题.
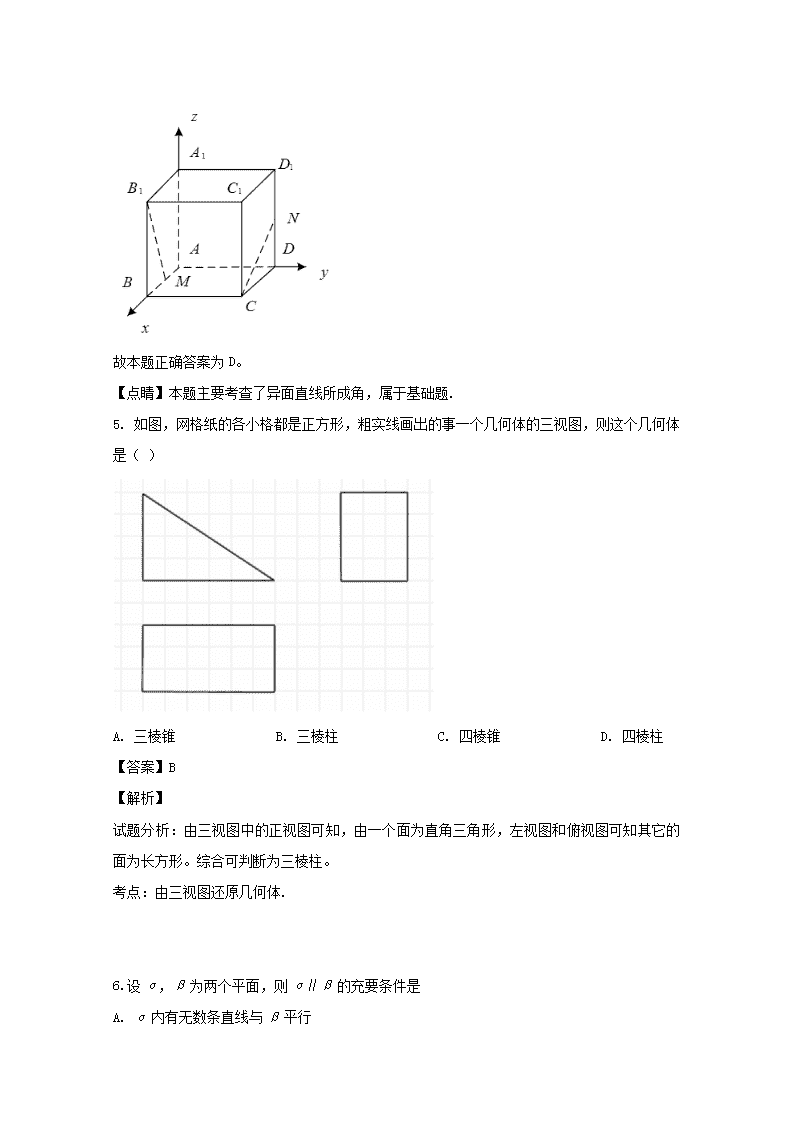
4.正方体ABCD—A′B′C′D′中,AB的中点为M,DD′的中点为N,则异面直线B′M与CN所成角的大小为
A. 0° B. 45° C. 60 ° D. 90°
【答案】D
【解析】
【分析】
以为原点,为 轴, 为轴,为轴建立空间直角坐标系,利用向量,的数量积为0,即可求解.
【详解】以为原点,为 轴, 为轴,为轴建立空间直角坐标系如图所示,
设正方体的棱长为,
由图可知,,,,
所以,
所以
所以异面直线与所成角为。
故本题正确答案为D。
【点睛】本题主要考查了异面直线所成角,属于基础题.
5. 如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( )
A. 三棱锥 B. 三棱柱 C. 四棱锥 D. 四棱柱
【答案】B
【解析】
试题分析:由三视图中的正视图可知,由一个面为直角三角形,左视图和俯视图可知其它的面为长方形。综合可判断为三棱柱。
考点:由三视图还原几何体.
6.设α,β为两个平面,则α∥β的充要条件是
A. α内有无数条直线与β平行
B. α内有两条相交直线与β平行
C. α,β平行于同一条直线
D. α,β垂直于同一平面
【答案】B
【解析】
【分析】
本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.
【详解】由面面平行的判定定理知:内两条相交直线都与平行是的充分条件,由面面平行性质定理知,若,则内任意一条直线都与平行,所以内两条相交直线都与平行是的必要条件,故选B.
【点睛】面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,则”此类的错误.
7.若直线mx+ny+3=0在y轴上的截距为-3,且它的倾斜角是直线的倾斜角的2倍,则( )
A. ,n=1 B. ,n=-3
C. ,n=-3 D. ,n=1
【答案】D
【解析】
对于直线,令得,即
∴
∵的斜率为,直线的倾斜角是直线的倍
∴直线的倾斜角为,即
∴
故选D
8.设等比数列中,前n项和为,已知,,则
A. B. C. D.
【答案】C
【解析】
试题分析:因为等比数列,故也成等比数列,所以
考点:等比数列的性质
9.如图给出的是计算的值的一个程序框图,则判断框内应填入的条件是( )
A. B. C. D.
【答案】A
【解析】
由算法流程图所提供的算法程序可知:当时,,运算程序结束,所以当时运算程序不再继续,故应填,应选答案A。
10.已知是定义域为的奇函数,满足.若,则( )
A. B. C. D.
【答案】C
【解析】
分析:先根据奇函数性质以及对称性确定函数周期,再根据周期以及对应函数值求结果.
详解:因为是定义域为的奇函数,且,
所以,
因此,
因为,所以,
,从而,选C.
点睛:函数的奇偶性与周期性相结合的问题多考查求值问题,常利用奇偶性及周期性进行变换,将所求函数值的自变量转化到已知解析式的函数定义域内求解.
11.经过点作直线,若直线l与连接、的线段总有公共点,则直线的倾斜角的取值范围为( )
A B.
C. D.
【答案】A
【解析】
【分析】
因为直线l与连接、的线段总有公共点,可得,再利用斜率公式即可计算得出直线l的斜率的范围,再由直线的斜率与倾斜角之间的关系得出直线的倾斜角的范围.
【详解】因,所以。
因为直线l与连接、的线段总有公共点,
,
,
设直线l的倾斜角为,所以,所以,
又因为,所以,
故选:A.
【点睛】本题考查直线的倾斜角与直线的斜率之间的关系,对于此类问题注意从正切函数的图象与性质着手能快速地求解,属于中档题.
12.已知函数f(x)=2x-1,g(x)=1-x2,规定:当|f(x)|≥g(x)时,h(x)=|f(x)|;当|f(x)|