专题3-1+导数概念及其几何意义（练）-2018年高考数学一轮复习讲练测（浙江版） 8页

A基础巩固训练 ‎1.若曲线在点处的切线方程是，则（ ）‎ A．， ‎ B．， ‎ C．， ‎ D．， ‎ ‎【答案】A ‎【解析】‎ ‎2.【2017四川成都摸底】曲线在点处的切线方程是（ ）‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】‎ ‎，，，曲线在点处的切线方程是，故选A.‎ ‎3.已知，是的导函数，即，，…，，，则 ( ) ‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】因为，所以，‎ 可知的解析式周期为4，因为，所以,故选D.‎ ‎4.函数的导数是 ‎ ‎【答案】, ‎ ‎【解析】根据乘法的导数法则及常见函数的导数公式可得.‎ ‎5.【2017福建4月质检】已知定义在上的函数满足，且当时， ，则曲线在处的切线方程是__________．‎ ‎【答案】‎ B能力提升训练 ‎1．曲线在点处的切线为（ ）‎ A. B. C. D. 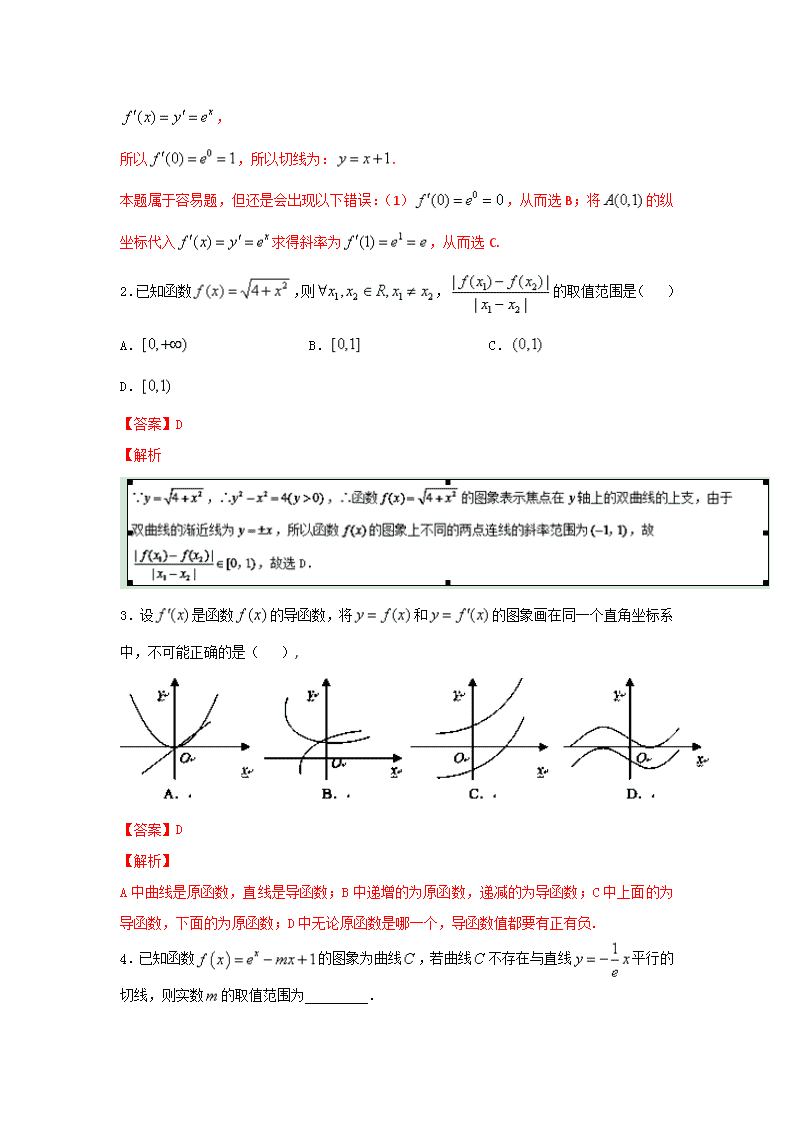‎ ‎【答案】A ‎【解析】函数在点处的切线方程：.在本题中，‎ ‎，‎ 所以，所以切线为：.‎ 本题属于容易题，但还是会出现以下错误：（1），从而选B；将的纵坐标代入求得斜率为，从而选C.‎ ‎2．已知函数，则，的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析 ‎3．设是函数的导函数，将和的图象画在同一个直角坐标系中，不可能正确的是（ ）, ‎ ‎【答案】D ‎【解析】‎ A中曲线是原函数，直线是导函数；B中递增的为原函数，递减的为导函数；C中上面的为导函数，下面的为原函数；D中无论原函数是哪一个，导函数值都要有正有负.‎ ‎4．已知函数的图象为曲线，若曲线不存在与直线平行的切线，则实数的取值范围为 ．‎ ‎【答案】‎ ‎【解析】‎ ‎，因为曲线不存在与直线平行的切线，所以方程无解，即无解，设，则，所以单调递增，所以，所以实数的取值范围为.‎ ‎5．若存在过点的直线与曲线和都相切，求的值.‎ ‎【答案】或．‎ ‎ C 思维拓展训练 ‎1.设曲线在点(3,2)处的切线与直线有相同的方向向量,则a等于（ ）‎ A．- B． C. -2 D．2‎ ‎【答案】B ‎【解析】‎ 因为，，在点处的切线与直线有相同的方向向量，所以，，故选B. ‎ ‎2．曲线上的点到直线的最短距离是 （ ）‎ A. B. C. D.0 ‎ ‎【答案】A ‎【解析】设直线与曲线相切与点且与直线平行，由得，所以，因此直线，直线到的距离为.所以曲线上的点到直线的最短距离是.‎ ‎3.曲线与有两条公切线，则的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ ‎4．设点P、Q分别是曲线是自然对数的底数）和直线上的动点，则P、Q 两点间距离的最小值为 【来.源：全,品…中&高*考*网】 ‎ ‎【答案】‎ ‎【解析】‎ ‎，令，即，，令，显然是增函数，且，即方程只有一解，曲线在处的切线方程为，两平行线和间的距离为.‎ ‎5．已知函数.‎ ‎（Ⅰ）求函数在点处的切线方程；‎ ‎（Ⅱ）求过点的函数的切线方程.‎ ‎【答案】（Ⅰ）（Ⅱ）或 ‎【解析】‎ 试题解析：（Ⅰ）∵, ‎ ‎∴在点处的切线的斜率 ‎∴函数在点处的切线方程为即【来.源：全,品…中&高*考*网】‎ ‎（Ⅱ）设函数与过点的切线相切于点，则切线的斜率 ‎∴切线方程为，即 ‎∵点在切线上 ‎∴即 ‎∴，解得或 ‎∴所求的切线方程为或.‎ ‎【来.源：全,品…中&高*考*网】‎ ‎ ‎