- 3.11 MB
- 2021-04-14 发布
静宁一中 2019-2020 学年度第一学期高二级第三次试题(卷)
数学(文科)
时间:120 分钟 满分:150 分
一、选择题(每小题 5 分,共 12 小题 60 分)
1、已知 ,则 等于( )
A. B. C. D.
2、从装有红球、黑球和白球的口袋中摸出一个球,若摸出的球是红球的概率是 ,摸出的
球是黑球的概率是 ,那么摸出的球是白球或黑球的概率是( )
A. B. C. D.
3、向如图所示的正方形内随机地投掷飞镖,飞镖落在阴影部分内的概率为( )
A.
B.
C.
D.
4、已知回归直线的斜率的估计值为 ,样本点的中心为 ,则回归直线方程为( )
A. B. C. D.
5、 点 在直线 上; 点 在曲线 上,则使“ ”为真命题的一个点
是( )
A. B. C. D.
6、抛物线 的准线方程为( )
A. B. C. D.
7、已知函数 的导函数 的图象如图所示,则 的图象可能是
( )
A. B. C. D.
8、设 ,则“ ”是“ ”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
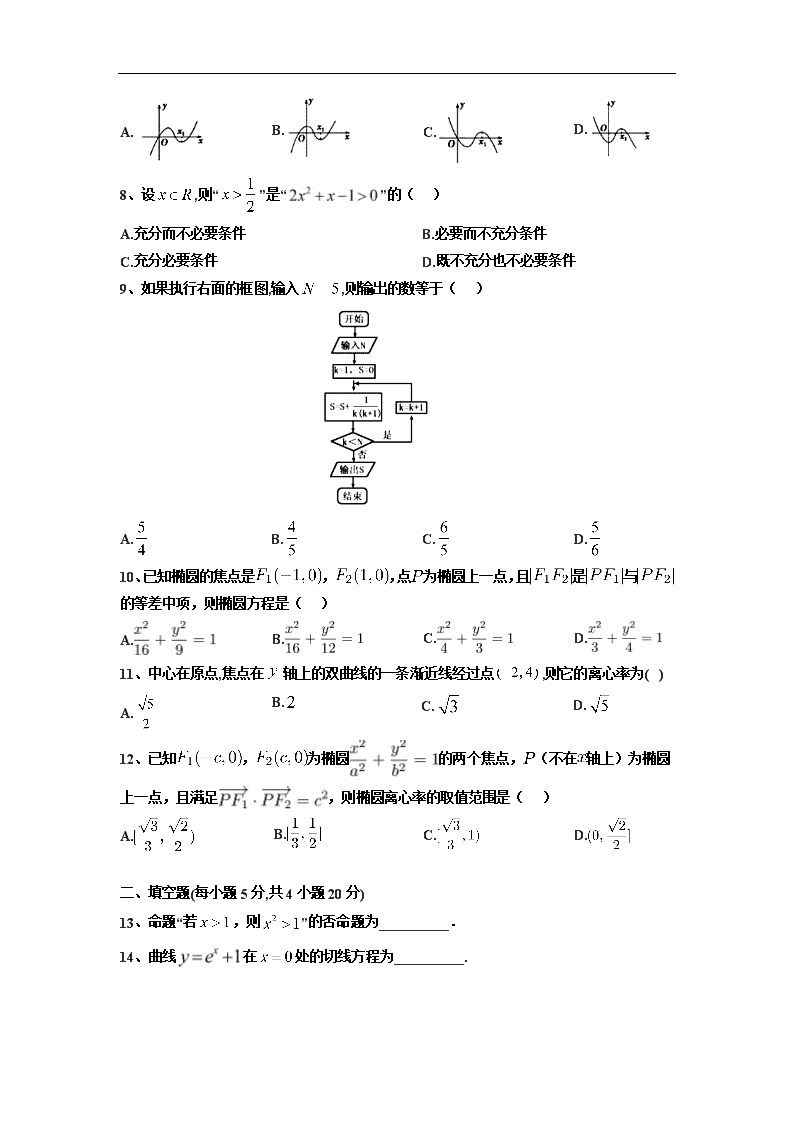
9、如果执行右面的框图,输入 ,则输出的数等于( )
A. B. C. D.
10、已知椭圆的焦点是 , ,点 为椭圆上一点,且 是 与
的等差中项,则椭圆方程是( )
A. B. C. D.
11、中心在原点,焦点在 轴上的双曲线的一条渐近线经过点 ,则它的离心率为( )
A. B. C. D.
12、已知 , 为椭圆 的两个焦点, (不在 轴上)为椭圆
上一点,且满足 ,则椭圆离心率的取值范围是( )
A. B. C. D.
二、填空题(每小题 5 分,共 4 小题 20 分)
13、命题“若 ,则 ”的否命题为__________.
14、曲线 在 处的切线方程为__________.
15、过点 作直线与双曲线 有且仅有一个公共点,这样的直线有________
条.
16、直线 经过抛物线 的焦点 ,且与抛物线交于 两点,若 ,则直
线 的斜率为__________.
三、解答题(第 17 题 10 分,第 18 题 12 分,第 19 题 12 分,第 20 题 12 分,第 21 题 12 分,第 22
题 12 分,共 6 小题 70 分)
17、一个袋中有四个形状大小完全相同的球,球的编号分别为 .
(1)从袋中随机取出两球,求取出两球的编号之和不大于 的概率.
(2)先从袋中随机取出一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取出一
个,该球的编号为 ,求 的概率.
18、已知函数 ,且 .
(1)求 的值;
(2)求函数 在 上的最大值和最小值.
19、省《体育高考方案》于 年 月份公布,方案要求以学校为单位进行体育测试,某校
对高
三班学按照高考测试项目按百分制进行了预备测试,并对 分以上的成绩进行统计,其频
率分布直方图如图所示,若 分数段的人数为 人.
(Ⅰ)请估计一下这组数据的平均数 ;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第
五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于 ,则称这两人为“帮扶
组”,试求选出的两人为“帮扶组”的概率.
20、已知抛物线 : 与直线 交于 两点.
(1)求弦 的长度;
(2)若点 在抛物线 上,且 的面积为 ,求点 的坐标.
21、已知函数 .
(1)求函数 的极值点;
(2)设函数 ,其中 ,求函数 在区间 上的最小值(其中
为自然对数的底数).
22、已知椭圆 的一个顶点是 ,离心率为 .
(1)求椭圆 的方程;
(2)已知矩形 的四条边都与椭圆 相切,设直线 AB 方程为 ,求矩形
面积的最小值与最大值.
静宁一中 2019-2020 学年度第一学期高二级第三次试题(卷)
数学(文)答案解析
第 1 题答案 C
第 1 题解析 , ,∴ .
第 2 题答案 D
第 2 题解析从袋中摸一个球,摸到的是红球,是白球,是黑球这三个事件是互斥的,因此摸出的球是
白球或黑球的概率为 .
第 3 题答案 B
第 3 题解析阴影部分内的面积 , ∴ .
第 4 题答案 C
第 4 题解析由回归直线的斜率的估计值为 ,可排除 D 由线性回归直线方程样本点的中心为
,将 分别代入 A、B、C,其值依次为 ,排除 A、B .
第 5 题答案 B
第 5 题解析点 的坐标满足 解得 或 .
第 6 题答案
第 6 题解析由题意,抛物线 ,可知 ,且开口向上,所以其准线方程为 .
第 7 题答案 D
第 7 题解析由图可知,设导函数的两个零点为 , ,则原函数在 单调递减, 单调递增,
单调递减,由图可知选项 D 正确.
第 8 题答案 A
第 8 题解析 由题意得,不等式 ,解得 或 ,所以“ ”是
“ ”的充分而不必要条件,故选 A.
第 9 题答案 D
第 9 题解析 初始值 , ,循环下去, , 成立; , , 成立;
, , 成立; , , 成立; ,
, 不成立,输出 .
第 10 题答案 C
第 10 题解析 由题意知: ,又∵ ,∴ ,则
, , ,故椭圆的方程为 .
第 11 题答案 A
第 11 题解析 由题意可知,此双曲线的渐近线方程为 ,则渐近线 过点
,即 , ,所以 .故选 A.
第 12 题答案 A
第 12 题解析 由椭圆的定义,得 ,平方得
①.
由 ,∴ ②,
由余弦定理,得 ③,
由①②③,得 ,∴ , .
,∴ ,即 ,∴ .
则椭圆离心率的取值范围是 .故选 C.
第 13 题答案“若 ,则 ”
第 13 题解析命题“若 ,则 ”的否命题为“若 ,则 ”,
第 14 题答案
第 14 题解析 的导数为 ,可得曲线 在 处的切线斜率为 ,即
有切线方程为 .
第 15 题答案 4
第 15 题解析由题可知有两条直线与双曲线相切,有两条与渐近线平行,共 条.
第 16 题答案
第 16 题解析 依题意,抛物线 的焦点 ,
设直线 的方程为
由 ,得 ,设 , .
∴ , ,∵ ,∴ 即 ,∵ ,∴
,解得 或 ,∴ 或 ,又 ,将 代入解得
.
第 17 题答案略
第 17 题解析 (1)从袋中随机取出两球,其一切可能的结果组成的基本事件有:“和 ”,“和 ”,“和
”,“ 和 ”,“ 和 ”,“ 和 ”,共 个;编号之和不大于 的基本事件有“和 ”,“和 ”,共 个,所
以所求事件的概率 ;
(2)先从袋中随机取出一个球,记下编号为 ,将球放回袋中,然后再从袋中随机取出一个球,
记下编号为 ,其结果用 表示,共有 ,
, , ,
个基本事件,其中不满足 的事件有 ,共 个,满足条件的共有
个,所以满足条件 的事件概率 .
第 18 题答案(1) ;(2) .
第 18 题解析
(1)∵ , ,∴ .
(2)令 ,得 或 ;令 ,得 .
∴ 在 , 上单调递增;在 上单调递减.
∴极大值为 ,极小值为 ,
又 ,∴ .
第 19 题答案略
第 19 题解析(1)数学成绩的平均数为
(分).
低于 分的频率为 ,
低于 分的频率为 ,
设数学成绩的中位数为 分,则 ,解得 .
所以该年级同学数学成绩的中位数约为 .
(2)不低于 分的同学中,由频率分布直方图估计在 内的概率为 ,在
内的概率 ,所以按照分层抽样的方式抽出 名同学,应该从成绩在
内的同学中抽取 名,分别设为 , ,从成绩在 内的同学中抽取 名,设为 .
先后发言,共有 种等可能结果: , , , , , ,
其中在同一组的同学发言时顺序相邻的有 种结果: , , , .
所以选出的 名同学中同一组的同学发言时顺序相邻的概率为 .
第 20 题答案见解答.
第 20 题解析 1)设点 ,由 可得 ,解得 或 4,
∴点 两点的坐标为 ,故 .
(2)设点 ,点 到 的距离为 , ,
,所以 ,即 ,解得 或 ,
所以 点的坐标为 或 .
第 21 题答案(1) 是函数 的极小值点,无极大值点;(2)见解析.
第 22 题解析 (1) , ,由 ,得 ,
所以 在区间 上单调递减,在区间 上单调递增.
所以 是函数 的极小值点,无极大值点.
(2) ,则 ,由 ,得 .
所以在区间 上, 为减函数,在区间 上, 为增函数.
当 ,即 时,在区间 上, 为增函数,
所以 的最小值为 ;
当 ,即 时, 的最小值为 ;
当 ,即 时,在区间 上, 为减函数,所以 的最小值为 .
综上,当 时, 的最小值为 ;当 时, 的最小值为 ;当 时,
的最小值为 .
第 22 题答案(1) ;(2)当 时 有最大值 10;当 时, 有最小值 8.
第 22 题解析(1)由题意,椭圆 的一个顶点是 ,
所以 ,又离心率为 ,即 ,
解得 ,故椭圆 C 的方程是 ;
(2)当 时,椭圆的外切矩形 面积为 8.当 时,椭圆的外切矩形 的边 所在
直线方程为 ,所以,直线 BC 和 AD 的斜率均为 .
由 ,消去 y 得 ,
,
化简得: ,
所以,直线 AB 方程为 ,
直线 DC 方程为 ,
直线 AB 与直线 DC 之间的距离为 ,
同理,可求 BC 与 AD 距离为 ,
则矩形 ABCD 的面积为
由均值定理 ,
仅当 ,即 时 有最大值 10.
因此,当 时 有最大值 10;当 时, 有最小值 8.