- 849.50 KB
- 2021-04-14 发布
内蒙古鄂尔多斯市一中2018~2019学年度第二学期期末考试试题
高二数学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~23题为选考题,其它题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.考生必须按照题号在答题卡各题号相对应的答题区域内(黑色线框)作答,写在草稿纸上、超出答题区域或非题号对应的答题区域的答案一律无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
第I卷
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,则
A. B. C. D.
2.i是虚数单位,复数z满足(1+i)z=1+3i,则z=
A.1+2i B.1-2i C. 2+i D.2-i
3.已知双曲线的离心率为,则此双曲线的渐近线方程为
A. B. C. D.
4.设函数在R上为增函数,则下列结论一定正确的是
A.在R上为减函数 B.在R上为增函数
C.在R上为增函数 D.在R上为减函数
5.从(40,30), (50,10), (20,30),(45,5),(10,10)中任取一个点,这个点在圆内部的概率是
A. B. C. D.
6.定义矩阵,若,则的图象向右平移个单位得到函数,则函数解析式为
A. B.
C. D.
7.已知,函数的图像经过点,则的最小值为
A. B.6 C. D.8
8.若点P在抛物线上,点Q(0,3),则|PQ|的最小值是
A. B. C. D.
9.以下四个命题中,真命题的个数是
①“若,则,中至少有一个不小于”的逆命题;
② 存在正实数a,b,使得
③ ;
④ 函数是奇函数,则的图像关于对称.
A. 0 B. 1 C. 2 D. 3
10.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能是
A. B. C. D.
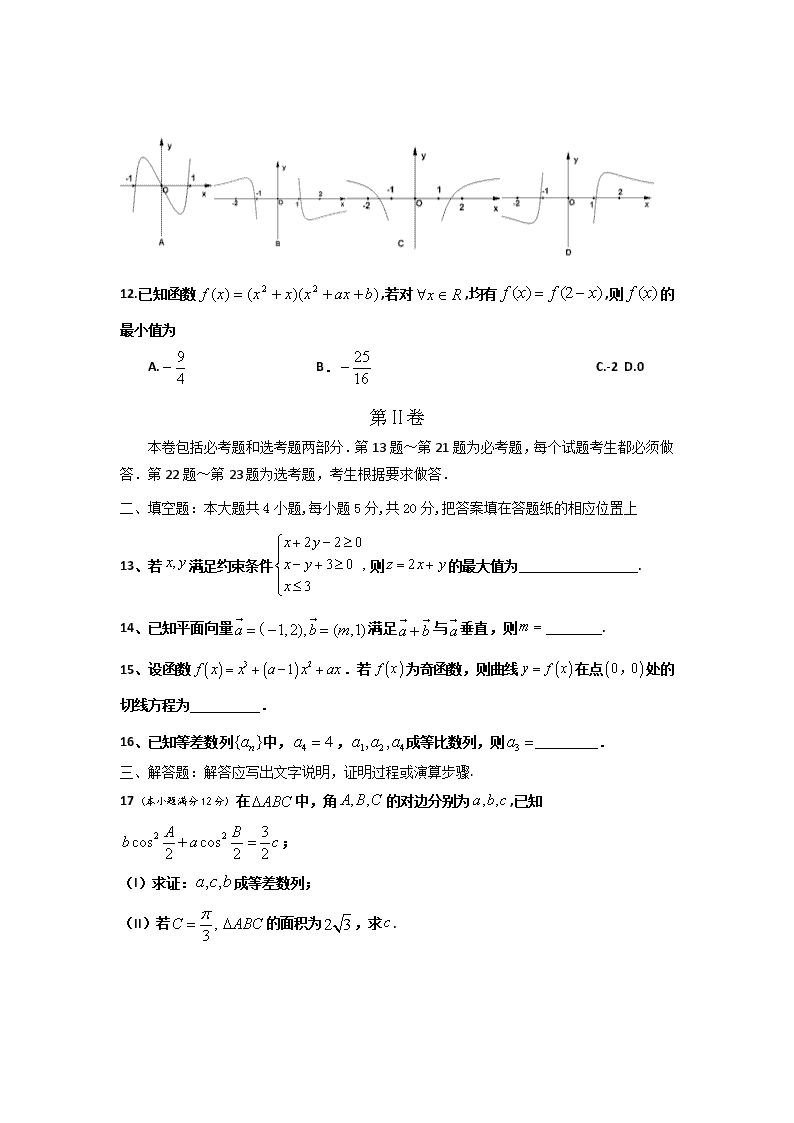
11.函数的图象大致为
12.已知函数,若对,均有,则的最小值为
A. B. C.-2 D.0
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第23题为选考题,考生根据要求做答.
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题纸的相应位置上
13、若满足约束条件则的最大值为 .
14、已知平面向量满足与垂直,则________.
15、设函数.若为奇函数,则曲线在点处的切线方程为__________.
16、已知等差数列中,,成等比数列,则_________.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17 (本小题满分12分) 在中,角的对边分别为,已知;
(I)求证:成等差数列;
(II)若的面积为,求.
18(本小题满分12分)某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:
(I)分别估计该市的市民对甲、乙两部门评分的中位数;
(II)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(III)根据茎叶图分析该市的市民对甲、乙两部门的评价.
19(本小题满分12分)如图,在三棱锥中,,,,,为线段的中点,为线段上一点.
(I)求证:平面平面;
(II)当平面时,求三棱锥的体积.
20(本小题满分12分)已知椭圆满足:过椭圆的右焦点且经过短轴端点的直线的倾斜角为.
(Ⅰ)求椭圆的方程;
(Ⅱ)设为坐标原点,若点在直线上,点在椭圆上,且,求线段长度的最小值.
21(本小题满分12分)已知函数其中
(Ⅰ)求的单调区间;
(Ⅱ)若在上存在,使得成立,求的取值范围.
选做题: 请考生从第22、23两题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分.
22 (本题满分10分)选修4-4:坐标系与参数方程
在直角坐标系中,圆C的参数方程为(为参数).
(I)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(II)已知A(-2, 0),B(0,2),圆C上任意一点M(x, y),求ABM面积的最大值.
23(本题满分10分)选修4-5:不等式选讲
设
(I)解不等式
(II)若不等式在上恒成立,求实数k的取值范围.
高二文科数学答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
D
C
C
D
B
A
D
B
D
C
B
A
12
7
3或4
17. 解(1)证明:由正弦定理得:
即,……2分
,……4分
……5分 成等差数列. ……6分
(2) ……8分
……10分 得…12分
18. 解:(I)由所给茎叶图知,50位市民对甲部门的评分由小到大排序,排在第25,26位的是75,75,故样本中位数为75,所以该市的市民对甲部门评分的中位数的估计值是75 .………………2分
50位市民对乙部门的评分由小到大排序,排在第25,26位的是66,68,故样本中位数为,所以该市的市民对乙部门评分的中位数的估计值是67. ………………4分
(Ⅱ)由所给茎叶图知,50位市民对甲、乙部门的评分高于90的比率分别为,,故该市的市民对甲、乙部门的评分高于90的概率的估计值分别为0.1,0.16. ………………8分
(Ⅲ)由所给茎叶图知,市民对甲部门的评分的中位数高于对乙部门的评分的中位数,而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门的评价较低、评价差较大。(注:考生利用其他统计量进行分析,结论合理的同样给分。)……………12分
19. (1)证明:, 平面又平面 ……2分
,为线段的中点 ……3分
又平面……5分 平面 平面平面 ……6分
(2)平面,平面平面 ……8分
为中点 为中点……9分
三棱锥的体积为 ……12分
20.解:(1)设椭圆的短轴端点为(若为上端点则倾斜角为钝角),则过右焦点与短轴端点的直线的斜率, ………………4分
(2)设点的坐标分别为,其中,即就是,………6分
解得.又……10分
,且当时等号成立,所以长度的最小值为………………12分
21. 解:(1). ………………2分
当时,在上在上单调递增;………………4分
当时,在上;在上;所以在
上单调递减,在上单调递增. ………………6分
综上所述,当时,的单调递增区间为;当时,的单调递减区间为,单调递增区间为.………………7分
(2) 若在上存在,使得成立,则在上的最小值小于0.………………8分
①当,即时,由(1)可知在上单调递增,在上的最小值为,由,可得………………9分
②当,即时,由(1)可知在上单调递减,在上的最小值为,由,可得………………10分
③当,即时,由(1)可知在上单调递减,在上单调递增,在上的最小值为,因为,所以,即,即,不满足题意,舍去. ………………11分
综上所述,实数a的取值范围为.………………12分
22. 解:(1)圆C的参数方程为(为参数),
圆C的普通方程为,所以圆C的极坐标方程为…5分
(2)易求直线AB方程为,,点M(x, y)到直线AB:的距离为
ABM的面积
ABM的面积最大值为.……10分
24. 解:(1)可转化为①或②
或③
解①得 解②得 解③得 原不等式的解集为 ……5分
(2)时,
不等式在上恒成立,在上恒成立
在上恒成立.设,在是上为增函数
. ……10分