北师大版初中数学 数怎么又不够用了(2课时)教案 5页

‎ ‎ ‎2.1数怎么又不够用了(二)‎ 教学目标：‎ ‎(一)教学知识点 ‎1.借助计算器探索无理数是无限不循环小数，并从中体会无限逼近的思想.‎ ‎2.会判断一个数是有理数还是无理数.‎ ‎(二)能力训练要求 ‎1.借助计算器进行估算，培养学生的估算能力，发展学生的抽象概括能力，并在活动中进一步发展学生独立思考、合作交流的意识和能力.‎ ‎2.探索无理数的定义，以及无理数与有理数的区别，并能辨别出一个数是无理数还是有理数，训练大家的思维判断能力.‎ ‎(三)情感与价值观要求 ‎1.让学生理解估算的意义，掌握估算的方法，发展学生的数感和估算能力.‎ ‎2.充分调动学生的积极性，培养他们的合作精神，提高他们的辨识能力.‎ 教学重点：‎ ‎1.无理数概念的探索过程.‎ ‎2.用计算器进行无理数的估算.‎ ‎3.了解无理数与有理数的区别，并能正确地进行判断.‎ 教学难点：‎ ‎1.无理数概念的建立及估算.‎ ‎2.用所学定义正确判断所给数的属性.‎ 教学过程：‎ Ⅰ.创设问题情境，引入新课 ‎［师］同学们，我们在上节课了解到有理数又不够用了，并且我们还发现了一些数，如a2=2,b2=5中的a，b既不是整数，也不是分数，那么它们究竟是什么数呢？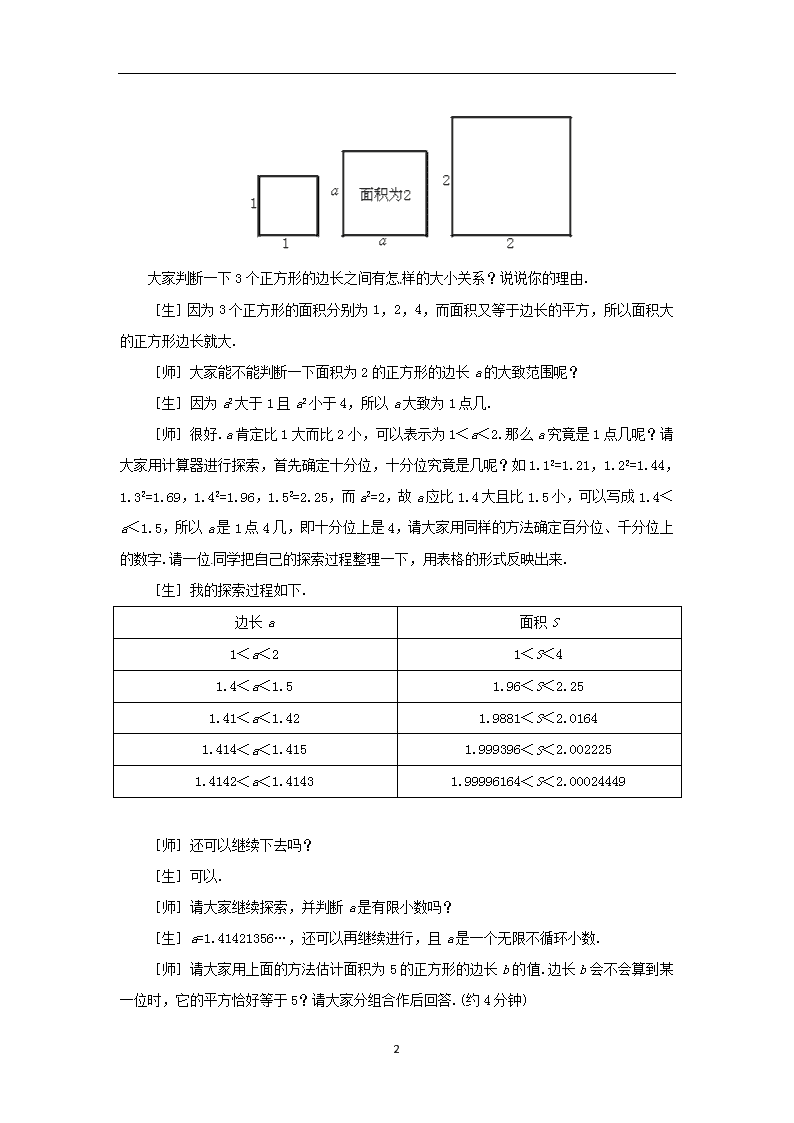本节课我们就来揭示它的真面目.‎ Ⅱ.讲授新课 ‎1.导入 ‎［师］请看图 5‎ ‎ ‎ 大家判断一下3个正方形的边长之间有怎样的大小关系？说说你的理由.‎ ‎［生］因为3个正方形的面积分别为1，2，4，而面积又等于边长的平方，所以面积大的正方形边长就大.‎ ‎［师］大家能不能判断一下面积为2的正方形的边长a的大致范围呢？‎ ‎［生］因为a2大于1且a2小于4，所以a大致为1点几.‎ ‎［师］很好.a肯定比1大而比2小，可以表示为1＜a＜2.那么a究竟是1点几呢？请大家用计算器进行探索，首先确定十分位，十分位究竟是几呢？如1.12=1.21，1.22=1.44，1.32=1.69，1.42=1.96，1.52=2.25，而a2=2，故a应比1.4大且比1.5小，可以写成1.4＜a＜1.5，所以a是1点4几，即十分位上是4，请大家用同样的方法确定百分位、千分位上的数字.请一位同学把自己的探索过程整理一下，用表格的形式反映出来.‎ ‎［生］我的探索过程如下.‎ 边长a 面积S ‎1＜a＜2‎ ‎1＜S＜4‎ ‎1.4＜a＜1.5‎ ‎1.96＜S＜2.25‎ ‎1.41＜a＜1.42‎ ‎1.9881＜S＜2.0164‎ ‎1.414＜a＜1.415‎ ‎1.999396＜S＜2.002225‎ ‎1.4142＜a＜1.4143‎ ‎1.99996164＜S＜2.00024449‎ ‎［师］还可以继续下去吗？‎ ‎［生］可以.‎ ‎［师］请大家继续探索，并判断a是有限小数吗？‎ ‎［生］a=1.41421356…，还可以再继续进行，且a是一个无限不循环小数. ‎ ‎［师］请大家用上面的方法估计面积为5的正方形的边长b的值.边长b会不会算到某一位时，它的平方恰好等于5？请大家分组合作后回答.(约4分钟)‎ 5‎ ‎ ‎ ‎［生］b=2.236067978…，还可以再继续进行，b也是一个无限不循环小数.‎ ‎2.无理数的定义 请大家把下列各数表示成小数.‎ ‎3，，并看它们是有限小数还是无限小数，是循环小数还是不循环小数.大家可以每个小组计算一个数，这样可以节省时间.‎ ‎［生］3=3.0，=0.8，=，‎ ‎，‎ ‎［生］3，是有限小数，是无限循环小数.‎ ‎［师］上面这些数都是有理数，所以有理数总可以用有限小数或无限循环小数表示.反过来，任何有限小数或无限循环小数都是有理数.‎ 像上面研究过的a2=2,b2=5中的a，b是无限不循环小数.‎ 无限不循环小数叫无理数(irrational number).‎ 除上面的a，b外，圆周率π=3.14159265…也是一个无限不循环小数，0.5858858885…(相邻两个5之间8的个数逐次加1)也是一个无限不循环小数，它们都是无理数.‎ ‎3.有理数与无理数的主要区别 ‎(1)无理数是无限不循环小数，有理数是有限小数或无限循环小数.‎ ‎(2)任何一个有理数都可以化为分数的形式，而无理数则不能.‎ ‎4.例题讲解 下列各数中，哪些是有理数？哪些是无理数？‎ ‎3.14，－，，0.1010010001…(相邻两个1之间0的个数逐次加1).‎ Ⅲ.课堂练习 ‎(一)随堂练习下列各数中，哪些是有理数？哪些是无理数？0.4583，，－π，－，18.‎ ‎ (二)补充练习：①、判断题 ‎(1)有理数与无理数的差都是有理数.‎ ‎(2)无限小数都是无理数.‎ ‎(3)无理数都是无限小数.‎ 5‎ ‎ ‎ ‎(4)两个无理数的和不一定是无理数.‎ ‎②、下列各数中，哪些是有理数？哪些是无理数？‎ ‎0.351，－，3.14159，－5.2323332…，123456789101112…(由相继的正整数组成).‎ 在下列每一个圈里，至少填入三个适当的数.‎ Ⅳ.课时小结 本节课我们学习了以下内容.‎ ‎1.用计算器进行无理数的估算.‎ ‎2.无理数的定义.‎ ‎3.判断一个数是无理数或有理数.‎ Ⅴ.课后作业 ‎1.P30习题2.2.‎ Ⅵ.探究与活动 设面积为5π的圆的半径为a.‎ ‎(1)a是有理数吗？说说你的理由.‎ ‎(2)估计a的值(精确到十分位，并利用计算器验证你的估计).‎ ‎(3)如果精确到百分位呢？‎ 解：∵πa2=5π ‎∴a2=5‎ ‎(1)a不是有理数，因为a既不是整数，也不是分数，而是无限不循环小数.‎ ‎(2)估计a≈2.2.‎ ‎(3)a≈2.24.‎ 板书设计：‎ 5‎ ‎ ‎ ‎2.1数怎么又不够用了（二）‎ 一、导入 二、新课 ‎1.无理数的定义 ‎2.举例 三、练习 四、补充练习 五、课时小节 六、课后作业 教学反思：这节内容是无理数的概念以及实数的分类。是数的范围的又一次扩充。是很重要的一节。培养学生的分类归纳的思想。但对概念的理解掌握一些同学还是不很好。只能在以后的教学过程中不断的加深。‎ 5‎