- 1.16 MB
- 2021-04-14 发布
1.7.2
定积分在物理中的应用
类型
1
:
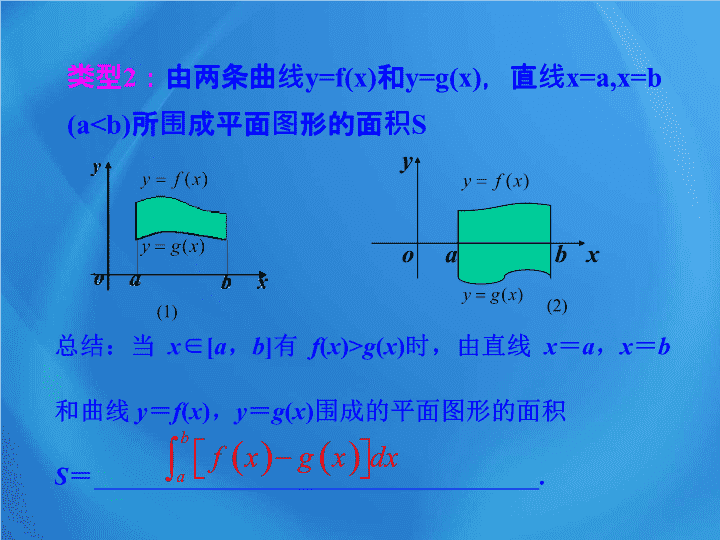
求由一条曲线
y=f(x)
和直线
x=a,x=b(a4
时,
P
点向
x
轴负方向运动.
故
t
=
3
时,点
P
离开原点的路程
s
1
=
(8t
-
2t
2
)dt
=
(4t
2
-
t
3
)|
=
18.
(2)
当
t
=
5
时,点
P
离开原点的位移
s
2
=
(8t
-
2t
2
)dt
=
(4t
2
-
t
3
)|
=
.
所以
点
P
在
x
轴正方向上距离原点
处.
(3)
从
t
=
0
到
t
=
5
时,点
P
经过的路程
s
3
=
(8t
-
2t
2
)dt
-
(8t
-
2t
2
)dt
=
(4t
2
-
t
3
)|
-
(4t
2
-
t
3
)|
=
26.
(4)
依题意
(8t
-
2t
2
)dt
=
0
,
即
4t
2
-
t
3
=
0
,
解得
t
=
0
或
t
=
6
,
t
=
0
对应于
P
点刚开始从原点出发的情况,
t
=
6
是所求的值.
C
4
求下列曲线所围成的图形的面积
:
(1)y=x
2
,y=2x+3;
(2)y=e
x
,y=e,x=0.
解:
解:
建立坐标系如图
这一薄层水的重力为
(
焦
)
.
3
设物体运动的速度
v=v(t)
(v(t)≥0)
,则此物体在时间区间
[a, b]
内运动的路程
s
为
1.
变速直线运动的路程
2.
变力沿直线所做的功
物体在变力
F(x)
的作用下做直线运动,并且物体沿着与
F(x)
相同的方向从
x=a
点移动到
x= b
点,则变力
F(x)
所做的功为
:
再长的路,一步步也能走完,再短的路,不迈开双脚也无法到达
.