- 399.50 KB
- 2021-04-13 发布
2017-2018学年黑龙江省牡丹江市第一高级中学高二上学期期中考试文科数学试题
一、选择题(本大题共有12个小题,每小题5分,共60分,在每小题给出的四选项中只有一项是符合题目要求的。)
1.已知点在椭圆上,则( )
A. 点不在椭圆上 B. 点不在椭圆上
C. 点在椭圆上 D. 无法判断点, , 是否在椭圆上
2.设椭圆的左、右焦点分别为, 是上任意一点,则的周长
为( )
A. B. C. D.
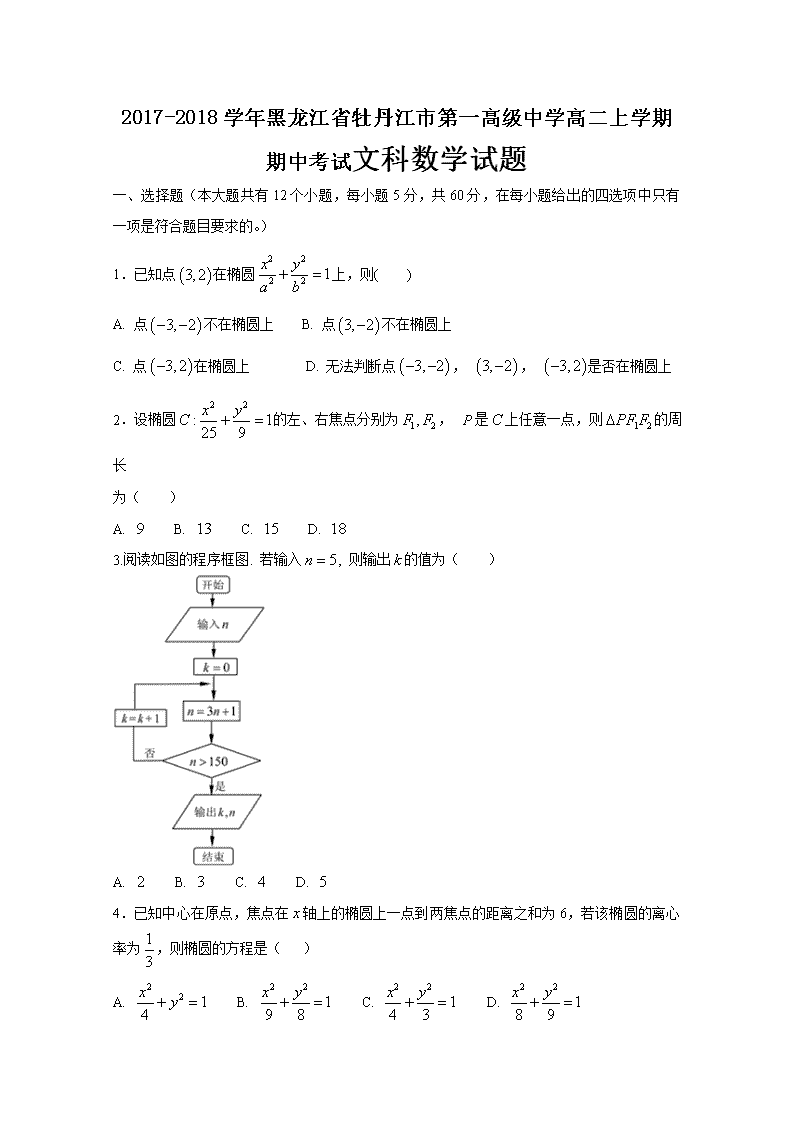
3.阅读如图的程序框图. 若输入, 则输出的值为( )
A. B. C. D.
4.已知中心在原点,焦点在轴上的椭圆上一点到两焦点的距离之和为6,若该椭圆的离心率为,则椭圆的方程是( )
A. B. C. D.
5.已知双曲线的一条渐近线方程为,它的焦距为8,则此双曲线的方程为( ).
A. B. C. D.
6.方程 (t为参数)表示的曲线是( )。
A. 一条直线 B. 两条射线 C. 一条线段 D. 抛物线的一部分
7. 把二进制的数11111(2)化成十进制的数为( )
A. 31 B. 15 C. 16 D. 11
8.已知双曲线的右焦点与抛物线的焦点重合,则该双曲线的离线率为( )
A. B. C. D.
9.抛物线的准线方程是( ).
A. B. C. D.
10.已知双曲线的中心为原点,点是双曲线的一个焦点,点到渐近线的距离
为1,则的方程为( )
A. B. C. D.
11.椭圆的焦点为,点在椭圆上,若,则的余弦值
为( )
A. B. C. D.
12.设抛物线的焦点为,过点的直线与抛物线相交于
两点,与抛物线的准线相交于点, ,则与的面积之比( )
A. B. C. D.
二、填空题(本大题共有4个小题,每小题5分,共20分)
13.在极坐标系中,点的坐标为,则点的直角坐标为__________.
14.已知椭圆与坐标轴依次交于四点,则四边形的面积为_______.
15.过抛物线的焦点且与轴垂直的直线交抛物线,则________.
16.是经过双曲线焦点且与实轴垂直的直线,是双曲线的两个顶点,若在上存在一点,使,则双曲线离心率的最大值为__________.
三、解答题(本大题共有6个小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(10分)已知曲线的参数方程为(为参数),以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.把的参数方程式化为普通方程, 的极坐标方程式化为直角坐标方程。
18.(12分)求与椭圆有相同的焦距,且离心率为的椭圆的标准方程。
19.(12分)已知直线:,圆C的极坐标方程为.
(Ⅰ)求圆C在直角坐标方程;
(Ⅱ)若圆C与直线相切,求实数的值。
20. (12分)在抛物线上找一点,使到直线的距离最短。
21. (12分)以直角坐标系的原点为极点,轴的非负半轴为极轴建立极坐标系,已知曲线的极坐标方程为.
(1)求曲线的直角坐标方程;
(2)若直线l的参数方程为(为参数),设点,直线l与曲线相交于两点,求的值。
22.(12分)椭圆的离心率为,右顶点为.
(Ⅰ)求椭圆方程.
(Ⅱ)该椭圆的左右焦点分别为,过的直线l与椭圆交于点A、B,且面积为,求直线l的方程。
2017—2018上学期期中考试高二文科数学参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
B
C
C
A
D
B
A
A
D
题号
13
14
15
16
答案
30
6
17.,
18.
19.(1);(2)-3或1。
20.
21. (1)由曲线C的原极坐标方程可得,化成直角方程为.
(2)联立直线线l的参数方程与曲线C方程可得,
整理得,
∵,于是点P在AB之间,
∴.
22. (Ⅰ)右顶点为,∴,∵,∴,∴,∴椭圆为.
(Ⅱ)设直线为,代入椭圆方程,∴,
整理得,
,.
∴.
∵,代入解出.
∴直线的方程为,.