- 160.00 KB
- 2021-04-13 发布
映射
一、考点突破
了解映射的概念及表示方法。
二、重难点提示
重点:理解映射的概念;
难点:理解象与原象的概念,会判断一些简单的对应是否是映射,会求象或原象。
◆ 映射的定义
设A,B是两个非空的集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有唯一的元素与之对应,那么这样的对应叫做从集合A到集合B的映射,记作:。
注意:
(1)要理解映射定义中的关键词;
(2)A中元素必须取完,B中元素可以取完,也可以不取完,这种对应可以是一对一,也可以是多对一,但不能是一对多;
(3)在映射中,集合A叫做映射的定义域,与A中元素x对应的B中元素y叫做x的象,记作:,x叫做y的原象。
◆ 映射的“三性”
1. “有序性”:映射是有方向的,从A到B的映射与从B到A的映射往往不是同一个映射;
2. “存在性”:对于集合A中的任何一个元素,集合B中都存在元素和它对应;
3. “唯一性”:对于集合A中的任何一个元素,在集合B中和它对应的元素是唯一的。
例题1 下列对应关系中,哪些是从A到B的映射,哪些不是?如果不是映射,如何修改可以使其成为映射?
(1)A=R,B=R,对应法则f:取倒数;
(2)A={平面内的三角形},B={平面内的圆},对应法则f:作三角形的外接圆。
思路分析:根据定义分析是否满足“A中元素的任意性”和“B中对应元素的唯一性”。
答案:(1)不是映射,集合A中的元素0在集合B中没有元素与之对应,不满足“A中任意性”;若把集合A改为A={x|x≠0}或者把对应法则f改为“加1”等,就可成为映射;
(2)是映射,集合A中的任意一个元素(三角形),在集合B中都有唯一的元素(该三角形的外接圆)与之对应,这是因为平面内不共线的三点可以确定一个圆。
技巧点拨:将不是映射的对应修改为映射,可以从出发集A、终止集B和对应法则f三个角度入手。
例题2 已知A=R,B={(x,y)|x,y
2
R},f:A→B是从集合A到集合B的映射,f:x→(x+1,x2+1),求A中的元素的象,B中元素的原象。
思路分析:把握好象与原象的关系,进而求象或原象。
答案:∵的映射关系为
∴A中元素的象为
故的原象为。
【思维拓展】
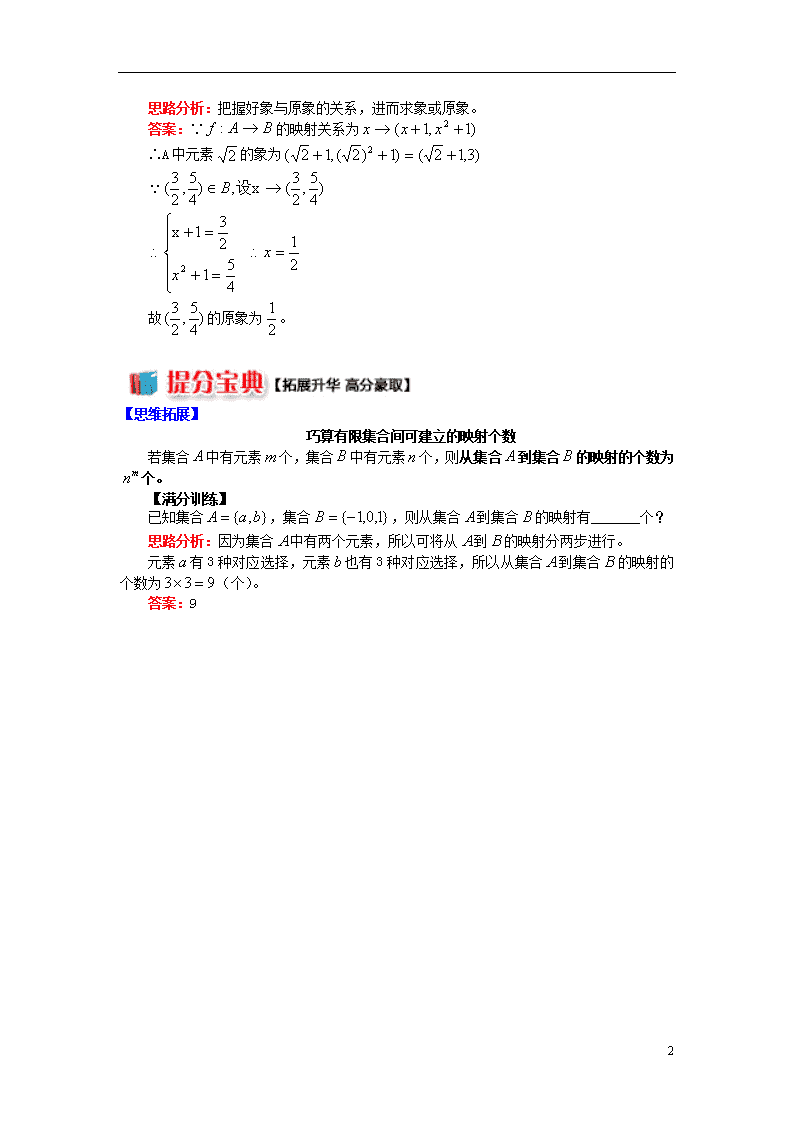
巧算有限集合间可建立的映射个数
若集合中有元素个,集合中有元素个,则从集合到集合的映射的个数为个。
【满分训练】
已知集合,集合,则从集合到集合的映射有_______个?
思路分析:因为集合中有两个元素,所以可将从到的映射分两步进行。
元素有3种对应选择,元素也有3种对应选择,所以从集合到集合的映射的个数为(个)。
答案:9
2
相关文档
- 精编202X年年度高中教师个人工作总2021-04-13 23:39:3714页
- 政教处工作总结范文之如何提高中学2021-04-13 23:39:055页
- 2020高中历史 课时跟踪训练12 新人2021-04-13 23:38:466页
- 高中语文精品课件雷雨12021-04-13 23:38:3220页
- 2019-2020学年新教材高中物理第1章2021-04-13 23:37:406页
- 高中数学第8章圆锥曲线方程(第18课2021-04-13 23:37:039页
- 高中地理第三章生产活动与地域联系2021-04-13 23:35:2117页
- 高中英语教案:必修二(Unit3 Computer2021-04-13 23:34:044页
- 高中数学必修4教案:2_备课资料(1_1_22021-04-13 23:33:203页
- 高中数学:《行线分线段成比例定理》2021-04-13 23:33:008页