2017-2018学年湖南省衡阳县高二下学期期末考试数学（文）试题-解析版 15页

绝密★启用前 湖南省衡阳县2017-2018学年高二下学期期末考试数学（文）试题 评卷人 得分 一、单选题 ‎1．已知集合A={1,2,3,4}，B={2,4,6,8}，则AB中元素的个数为 A． 1 B． 2 C． 3 D． 4‎ ‎【答案】B ‎【解析】由题意可得，故中元素的个数为2，所以选B.‎ ‎【名师点睛】集合基本运算的关注点：‎ ‎(1)看元素组成．集合是由元素组成的，从研究集合中元素的构成入手是解决集合运算问题的前提．‎ ‎(2)有些集合是可以化简的，先化简再研究其关系并进行运算，可使问题简单明了，易于解决．‎ ‎(3)注意数形结合思想的应用，常用的数形结合形式有数轴、坐标系和Venn图．‎ ‎2．设复数z满足，则＝（ ）‎ A． B． C． D． ‎ ‎【答案】C ‎【解析】由题意可得： .‎ 本题选择C选项.‎ ‎3．设实数，满足且，设实数，满足，则是的（ ）‎ A． 充分不必要条件 B． 必要不充分条件 C． 充要条件 D． 既不充分也不必要条件 ‎【答案】A ‎【解析】试题分析：“若且则”是真命题，其逆命题是假命题，故是的充分不必要条件,故选A.‎ 考点：充分必要条件.‎ 视频 ‎4． 执行如图所示的程序框图，输出S的值为（ ）‎ A． － B． C． － D． ‎ ‎【答案】D ‎【解析】试题分析：由已知可得，故选D.‎ 考点：程序框图.‎ 视频 ‎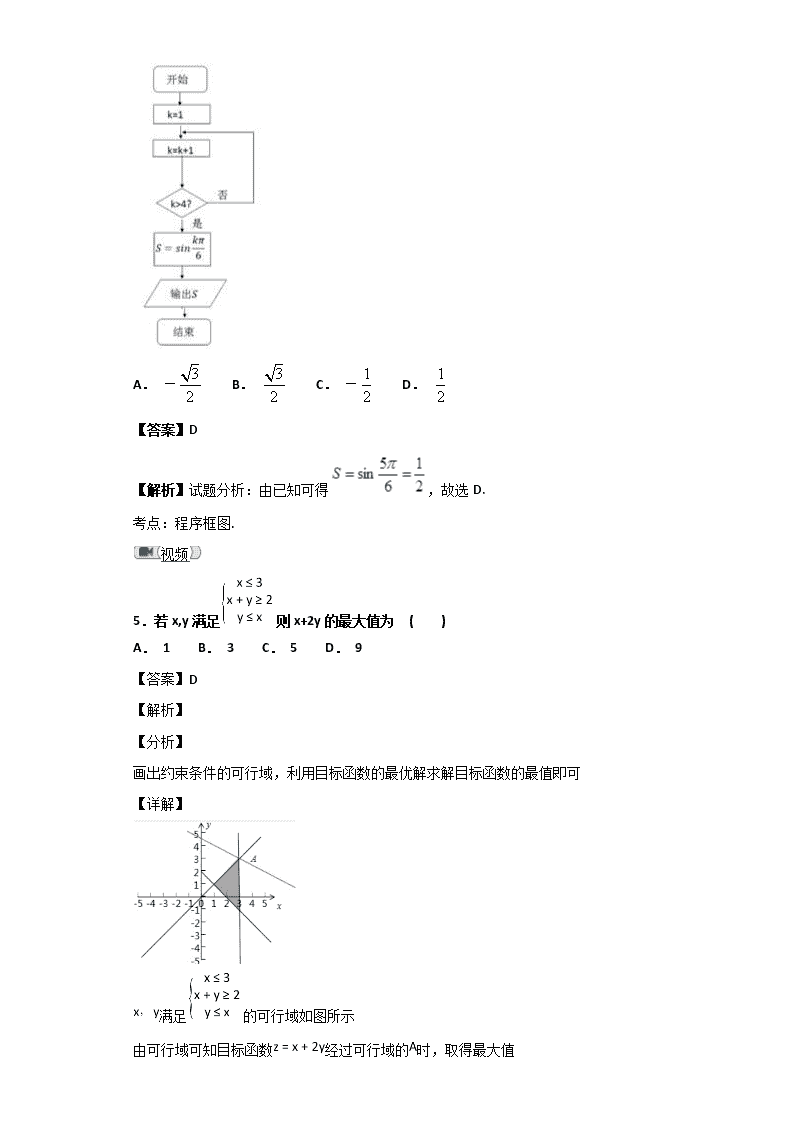5．若x,y满足则x+2y的最大值为　(　　)‎ A． 1 B． 3 C． 5 D． 9‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 画出约束条件的可行域，利用目标函数的最优解求解目标函数的最值即可 ‎【详解】‎ 满足的可行域如图所示 由可行域可知目标函数经过可行域的时，取得最大值 由，可得 目标函数的最大值为 故选 ‎【点睛】‎ 本题考查了简单的线性规划，解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义，属于基础题。‎ ‎6．函数的定义域为（ ）‎ A． (0,1) B． [0,1) C． (0,1] D． [0,1]‎ ‎【答案】B ‎【解析】‎ 选B.‎ 考点：该题主要考查函数的概念、定义域及其求法.‎ ‎7．甲、乙两人下棋，两人下成和棋的概率是，甲获胜的概率是，则甲不输的概率为（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎【解析】∵甲、乙两人下棋，两人下成和棋的概率是，甲获胜的概率是，‎ ‎∴甲不输的概率为P= ．‎ 故选项为：A．‎ ‎8．抛物线的准线方程是（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 先根据抛物线的标准方程得到焦点在轴上以及，再直接代入即可求出其准线方程 ‎【详解】‎ 抛物线的标准方程为，焦点在轴上 ‎，即 则准线方程为 故选 ‎【点睛】‎ 本题主要考查了抛物线的基本性质，先将其转换为标准方程，然后求出准线方程，属于基础题。‎ ‎9．设是等差数列的前项和,若,则 A． B． C． D． ‎ ‎【答案】A ‎【解析】，，选A.‎ 视频 ‎10．已知椭圆的左焦点为F1(－4,0)，则m等于 A． 9 B． 4 C． 3 D． 2‎ ‎【答案】C ‎【解析】因为左焦点为F1(－4,0)，‎ 所以 ，选C.‎ ‎11．在△ABC中，a=3，b=5，sinA=，则sinB=( )‎ A． B． C． D． 1‎ ‎【答案】B ‎【解析】‎ 试题分析：由正弦定理得，故选B．‎ 考点：正弦定理的应用 ‎12．函数的图像与函数的图像的交点个数为（ ）‎ A． 0 B． 1 C． 2 D． 3‎ ‎【答案】C ‎【解析】‎ 在同一直角坐标系下作出函数f(x)＝ln x与g(x)＝x2－4x＋4＝(x－2)2的图象，如图所示．‎ 由图知f(x)与g(x)的图象的交点个数为2，故选C.‎ 点睛：(1)图象法求函数零点个数的关键是正确画出函数的图象．在画函数的图象时，常利用函数的性质，如周期性、对称性等，同时还要注意函数定义域的限制．(2)对于一般函数零点个数的判断问题，不仅要判断区间[a，b]上是否有f(a)·f(b)<0，还需考虑函数的单调性．‎ 第II卷（非选择题）‎ 请点击修改第II卷的文字说明 评卷人 得分 二、填空题 ‎13．一个几何体的三视图如图所示（单位：)，则该几何体的体积为__________.‎ ‎【答案】.‎ ‎【解析】分析：首先根据题中所给的三视图，将几何体还原，分析得到其为一个圆柱和一个圆锥的组合体，所以其体积为圆柱和圆锥的体积之和，结合图中所给的数据，利用体积公式求得结果.‎ 详解：根据题中所给的几何体的三视图，将几何体还原，‎ 可以得到几何体是一个圆柱和圆锥的组合体，‎ 利用相关数据可知圆柱的体积为，圆 锥的体积为，‎ 所以该几何体的体积为，‎ 故答案是.‎ 点睛：该题考查的是有关根据几何体的三视图求其体积的问题，在解题的过程中，还原几何体是解题的关键，之后利用图中的相关数据，结合体积公式求得结果，注意组合体的体积在求解的时候将其分割，计算即可.‎ ‎14．若直线，过点，则的最小值为__________．‎ ‎【答案】8‎ ‎【解析】∵直线过点 ‎∴‎ ‎∴‎ ‎∵‎ ‎∴，当且仅当，即，时取等号 ‎∴的最小值为8‎ ‎15．若曲线在点处的切线经过坐标原点，则__________．‎ ‎【答案】2‎ ‎【解析】,则曲线在点（1,2）处的切线为: ,即,把（1,2）代入切线方程得: ,故填2.‎ 点睛:函数y＝f(x)在x＝x0处的导数的几何意义，就是曲线y＝f(x)在点P(x0，y0)处的切线的斜率，过点P的切线方程为： .求函数y＝f(x)在点P(x0，y0)处的切线方程与求函数y＝f(x)过点P(x0，y0)的切线方程意义不同，前者切线有且只有一条，且方程为y－y0＝f′(x0)(x－x0)，后者可能不只一条．‎ ‎16．已知点在圆上，点的坐标为，为原点，则的最大值为_________．‎ ‎【答案】6‎ ‎【解析】试题分析：所以最大值是6.‎ ‎【名师点睛】本题考查了转化与化归能力，因为是确定的，所以根据向量数量积的几何意义：若最大，即向量在 方向上的投影最大，根据数形结合分析可得当点在圆与轴的右侧交点处时最大，从而根据几何意义直接得到运算结果为.‎ 评卷人 得分 三、解答题 ‎17．已知向量，，，设函数．‎ ‎（Ⅰ）求的最小正周期；‎ ‎（Ⅱ）求在上的最大值和最小值．‎ ‎【答案】（1）（2）时，取最小值；时，取最大值1．‎ ‎【解析】试题分析：（1）根据向量数量积、二倍角公式及配角公式得，再根据正弦函数性质得．（2）先根据得，，再根据正弦函数性质得最大值和最小值．‎ 试题解析：（Ⅰ） ，‎ 最小正周期为．‎ ‎（Ⅱ）当时，，‎ 由图象可知时单调递增，时单调递减，‎ 所以当，即时，取最小值；‎ 当，即时，取最大值1．‎ 视频 ‎18．已知{an}是等差数列，{bn}是等比数列，且b2＝3，b3＝9，a1＝b1，a14＝b4.‎ ‎(1)求{an}的通项公式；‎ ‎(2)设cn＝an＋bn，求数列{cn}的前n项和．‎ ‎【答案】（1） （2） ‎ ‎【解析】试题分析：（Ⅰ）求出等比数列的公比，再求出a1，a14的值，根据等差数列的通项公式求解；‎ ‎（Ⅱ）根据等差数列和等比数列的前n项和公式求数列{cn}的前n项和.‎ 试题解析：（Ⅰ）等比数列的公比，‎ 所以， ．‎ 设等差数列的公差为．‎ 因为， ，‎ 所以，即．‎ 所以（， ， ， ）．‎ ‎（Ⅱ）由（Ⅰ）知， ， ．‎ 因此．‎ 从而数列的前项和 ‎．‎ ‎【考点】等差、等比数列的通项公式和前n项和公式，考查运算能力.‎ ‎【名师点睛】1.数列的通项公式及前n项和公式都可以看作项数n的函数，是函数思想在数列中的应用.数列以通项为纲，数列的问题，最终归结为对数列通项的研究，而数列的前n项和Sn可视为数列{Sn}的通项.通项及求和是数列中最基本也是最重要的问题之一；2.数列的综合问题涉及的数学思想：函数与方程思想（如：求最值或基本量）、转化与化归思想（如：求和或应用）、特殊到一般思想（如：求通项公式）、分类讨论思想（如：等比数列求和，或）等.‎ 视频 ‎19．如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.‎ ‎(1)求证:平面MOC⊥平面VAB．‎ ‎(2)求三棱锥V-ABC的体积.‎ ‎【答案】（1）见解析.‎ ‎（2）.‎ ‎【解析】‎ ‎【分析】‎ 先在中得到，再利用面面垂直的性质得到平面，最后利用面面垂直的判定得到结论 利用等体积法求三棱锥的体积 ‎【详解】‎ ‎(1)因为AC=BC,O为AB中点,所以OC⊥AB.‎ 因为平面VAB⊥平面ABC,交线AB,OC⊂平面ABC,所以OC⊥平面VAB.‎ 因为OC⊂平面MOC,所以平面MOC⊥平面VAB. ‎ ‎(2)由(1)知OC为三棱锥C-VAB的高,‎ 因为AC⊥BC且AC=BC=所以OC=1,AB=2.‎ 因为△VAB为等边三角形,所以S△VAB=×2×=.‎ ‎.‎ ‎【点睛】‎ 本题是一道关于面面垂直、求体积的题目，解题的关键是掌握面面垂直的性质定理和判定定理，在求棱锥的体积时需要运用等体积法进行转换，找出已知的高，本题考查了学生的空间想象能力，比较综合。‎ ‎20．某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：‎ 最高气温 ‎[10，15）‎ ‎[15，20）‎ ‎[20，25）‎ ‎[25，30）‎ ‎[30，35）‎ ‎[35，40）‎ 天数 ‎2‎ ‎16‎ ‎36‎ ‎25‎ ‎7‎ ‎4‎ 以最高气温位于各区间的频率代替最高气温位于该区间的概率.‎ ‎（1）求六月份这种酸奶一天的需求量不超过300瓶的概率；‎ ‎（2）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量为450瓶时，写出Y的所有可能值，并估计Y大于零的概率．‎ ‎【答案】（1）；（2）‎ ‎【解析】分析：（1）根据概率等于频数除以总数得结果，（2）先根据题意确定随机变量取法，再确定Y大于零实际意义，最后根据概率等于频数除以总数得结果.‎ 详解： ‎ ‎（1）最高气温低于25时这种酸奶的需求量不超过300‎ 则 ‎ ‎ （2）当最高气温不低于25时，需求量为500，进货450瓶均可售出 所以利润 （元）‎ 当最高气温位于区间[20，25），需求量为300瓶，进货450瓶只能售出300瓶 所以利润 （元）‎ 当最高气温低于20，需求量为200瓶，进货450瓶只能售出200瓶 所以利润 （元）‎ 当利润 时，最高气温不低于20，‎ 所以或者 点睛：在实际问题中经常以频率代替概率，而频率根据频数除以总数得到.‎ ‎21．椭圆（）的离心率是，点在短轴上，且。‎ ‎（1）球椭圆的方程；‎ ‎（2）设为坐标原点，过点的动直线与椭圆交于两点。是否存在常数，使得为定值？若存在，求的值；若不存在，请说明理由。‎ ‎【答案】（1）；（2）见解析.‎ ‎【解析】（Ⅰ）由已知，点C，D的坐标分别为（0，－b），（0，b）‎ 又点P的坐标为（0，1），且＝－1‎ 于是，解得a＝2，b＝‎ 所以椭圆E方程为.‎ ‎（Ⅱ）当直线AB斜率存在时，设直线AB的方程为y＝kx＋1‎ A，B的坐标分别为（x1，y1），（x2，y2）‎ 联立，得（2k2＋1）x2＋4kx－2＝0‎ 其判别式△＝（4k）2＋8（2k2＋1）＞0‎ 所以 从而＝x1x2＋y1y2＋λ[x1x2＋（y1－1）（y2－1）]‎ ‎＝（1＋λ）（1＋k2）x1x2＋k（x1＋x2）＋1‎ ‎＝‎ ‎＝－‎ 所以，当λ＝1时，－＝－3‎ 此时， ＝－3为定值 当直线AB斜率不存在时，直线AB即为直线CD 此时＝－2－1＝－3‎ 故存在常数λ＝－1，使得为定值－3.‎ 考点：本题主要考查椭圆的标准方程、直线方程、平面向量等基础知识，考查推理论证能力、运算求解能力，考查数形结合、化归与转化、特殊与一般、分类与整合等数学思想.‎ 视频 ‎22．[选修4—4:坐标系与参数方程]‎ 已知曲线C1的参数方程为 （为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为. ‎ ‎（Ⅰ）把C1的参数方程化为极坐标方程；‎ ‎（Ⅱ）求C1与C2交点的极坐标（ρ≥0,0≤θ＜2π）.‎ ‎【答案】(1) .‎ ‎(2) ，.‎ ‎【解析】‎ 试题分析：（1） 先根据同角三角函数关系cos2t＋sin2t=1消参数得普通方程：（x－4）2＋（y－5）2＝25 ，再根据将普通方程化为极坐标方程：（2）将代入得得，也可利用直角坐标方程求交点，再转化为极坐标 试题解析： （1）∵C1的参数方程为 ‎∴（x－4）2＋（y－5）2＝25（cos2t＋sin2t）＝25，‎ 即C1的直角坐标方程为（x－4）2＋（y－5）2＝25，‎ 把代入（x－4）2＋（y－5）2＝25，‎ 化简得：.[Z.X.X.K]‎ ‎（2）C2的直角坐标方程为x2＋y2＝2y，C1的直角坐标方程为（x－4）2＋（y－5）2＝25，‎ ‎∴C1与C2交点的直角坐标为（1，1），（0，2）.‎ ‎∴C1与C2交点的极坐标为.‎ 考点：参数方程化普通方程，直角坐标方程化极坐标方程 ‎23．[选修4—5:不等式选讲]‎ 已知函数 ‎(1)求不等式的解集.‎ ‎(2)若不等式的解集非空，求的取值范围.‎ ‎【答案】(1) [1,+∞).‎ ‎(2) .‎ ‎【解析】‎ 分析：（1）由绝对值的定义分类去掉绝对值符号后解一元一次不等式，最后合并可得解集；‎ ‎（2）不等式化为，利用绝对值的性质有 ‎，然后可利用二次函数性质求得其最大值，得到的取值范围．‎ 详解：（1）‎ 当时，无解；‎ 当时，由得，，解得；‎ 当时，由解得 所以的解集为 ‎（2）由得，而 ‎ ‎ 且当时，‎ 故的取值范围为 点睛：解含绝对值的不等式一般都是根据绝对值的定义分类去掉绝对值符号，然后再解不含绝对值的不等式，有时根据不等式的形貌直接由绝对值性质求解，如 ，或．‎