2018届二轮复习8-3空间点、直线、平面之间的位置关系课件（全国通用） 40页

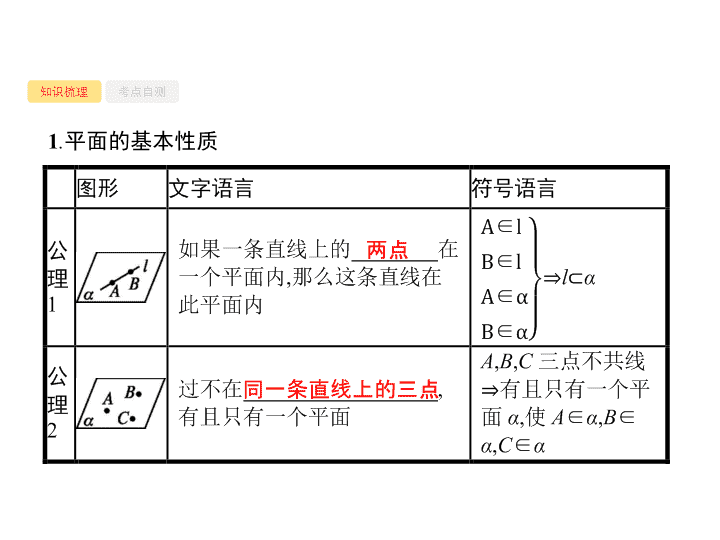
8 . 3 　 空间点、直线、平面之间 的位置关系 - 2 - - 3 - 知识梳理 考点自测 1 . 平面的基本性质 两点 同一条直线上的三点 - 4 - 知识梳理 考点自测 有且只有一条 - 5 - 知识梳理 考点自测 平行 相交 任何 锐角 ( 或直角 ) - 6 - 知识梳理 考点自测 4 . 等角定理 : 空间中如果两个角的两边分别对应平行 , 那么这两个角相等或互补 . 5 . 直线与平面的位置关系有平行、相交、在平面内三种情况 . 6 . 平面与平面的位置关系有平行、相交两种情况 . - 7 - 知识梳理 考点自测 1 . 公理 2 的三个推论 推论 1: 经过一条直线和这条直线外一点有且只有一个平面 . 推论 2: 经过两条相交直线有且只有一个平面 . 推论 3: 经过两条平行直线有且只有一个平面 . 2 . 异面直线判定的一个定理 过平面外一点和平面内一点的直线 , 与平面内不过该点的直线是异面直线 . - 8 - 知识梳理 考点自测 - 9 - 知识梳理 考点自测 1 . 判断下列结论是否正确 , 正确的画 “ √ ”, 错误的画 “ × ” . (1) 两个不重合的平面只能把空间分成四个部分 . ( 　　 ) (2) 两个平面 α , β 有一个公共点 A , 就说 α , β 相交于 A 点 , 记作 α ∩ β =A. ( 　　 ) (3) 已知 a , b 是异面直线 , 直线 c 平行于直线 a , 则 c 与 b 不可能是平行直线 . ( 　　 ) (4) 两个不重合的平面 α , β 有一条公共直线 a , 就说平面 α , β 相交 , 并记作 α ∩ β =a. ( 　　 ) (5) 若 a , b 是两条直线 , α , β 是两个平面 , 且 a ⊂ α , b ⊂ β , 则 a , b 是异面直线 . ( 　　 ) × × √ √ × - 10 - 知识梳理 考点自测 2 . 如图 , 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , E , F 分别为 BC , BB 1 的中点 , 则下列直线与直线 EF 相交的是 ( 　　 ) A. 直线 AA 1 B. 直线 A 1 B 1 C. 直线 A 1 D 1 D. 直线 B 1 C 1 D 解析 : 只有 B 1 C 1 与 EF 在同一平面内 , 是相交的 . 选项 A,B,C 中直线与 EF 都是异面直线 , 故选 D . - 11 - 知识梳理 考点自测 3 . 已知 a , b 是异面直线 , 直线 c 平行于直线 a , 则 c 与 b ( 　　 ) A. 一定是异面直线 B. 一定是相交直线 C. 不可能是平行直线 D. 不可能是相交直线 C 解析 : 由已知得 , 直线 c 与 b 可能为异面直线 , 也可能为相交直线 , 但不可能为平行直线 , 若 b ∥ c , 则 a ∥ b , 与已知 a , b 为异面直线相矛盾 . - 12 - 知识梳理 考点自测 4 . (2017 全国 Ⅰ , 文 6) 如图 , 在下列四个正方体中 , A , B 为正方体的两个顶点 , M , N , Q 为所在棱的中点 , 则在这四个正方体中 , 直线 AB 与平面 MNQ 不平行的是 ( 　　 ) A - 13 - 知识梳理 考点自测 解析 : 易知选项 B 中 , AB ∥ MQ , 且 MQ ⊂ 平面 MNQ , AB ⊄ 平面 MNQ , 则 AB ∥ 平面 MNQ ; 选项 C 中 , AB ∥ MQ , 且 MQ ⊂ 平面 MNQ , AB ⊄ 平面 MNQ , 则 AB ∥ 平面 MNQ ; 选项 D 中 , AB ∥ NQ , 且 NQ ⊂ 平面 MNQ , AB ⊄ 平面 MNQ , 则 AB ∥ 平面 MNQ. 故排除选项 B,C,D . 故选 A . - 14 - 知识梳理 考点自测 5 . 下列命题正确的个数为 　　　　　 .   ① 经过三点确定一个平面 ; ② 梯形可以确定一个平面 ; ③ 两两相交的三条直线最多可以确定三个平面 ; ④ 若两个平面有三个公共点 , 则这两个平面重合 . 2 解析 : 经过不共线的三点可以确定一个平面 , ∴① 不正确 ; 两条平行线可以确定一个平面 , ∴② 正确 ; 两两相交的三条直线可以确定一个或三个平面 , ∴③ 正确 ; 命题 ④ 中没有说清三个点是否共线 , ∴④ 不正确 . - 15 - 考点一 考点二 考点三 平面的基本性质及应用 例 1 (1) 如图所示 , 四边形 ABEF 和 ABCD 都是直角梯形 , ∠ BAD= ∠ FAB= 90 ° , , G , H 分别为 FA , FD 的中点 . ① 四边形 BCHG 的形状是 　　　　　 ;   ② 点 C , D , E , F , G 中 , 能共面的四点是 　　　　　 .   (2) 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , 对角线 A 1 C 与平面 BDC 1 交于点 O , AC 与 BD 交于点 M , 则点 O 与直线 C 1 M 的关系是 　　　　　 .   平行四边形 C , D , E , F 点 O 在直线 C 1 M 上 - 16 - 考点一 考点二 考点三 - 17 - 考点一 考点二 考点三 (2) 如图所示 , 因为 A 1 C ⊂ 平面 A 1 ACC 1 , O ∈ A 1 C , 所以 O ∈ 平面 A 1 ACC 1 , 而 O 是平面 BDC 1 与直线 A 1 C 的交点 , 所以 O ∈ 平面 BDC 1 , 所以点 O 在平面 BDC 1 与平面 A 1 ACC 1 的交线上 . 因为 AC ∩ BD=M , 所以 M ∈ 平面 BDC 1 . 又 M ∈ 平面 A 1 ACC 1 , 所以平面 BDC 1 ∩ 平面 A 1 ACC 1 =C 1 M , 所以 O ∈ C 1 M. - 18 - 考点一 考点二 考点三 思考 共面、共线、共点问题的证明有哪些方法 ? 解题心得 共面、共线、共点问题的证明 (1) 证明点或线共面问题的两种方法 : ① 首先由所给条件中的部分线 ( 或点 ) 确定一个平面 , 然后证其余的线 ( 或点 ) 在这个平面内 ; ② 将所有条件分为两部分 , 然后分别确定平面 , 再证两平面重合 . (2) 证明点共线问题的两种方法 : ① 先由两点确定一条直线 , 再证其他各点都在这条直线上 ; ② 直接证明这些点都在同一条特定直线上 . (3) 证明线共点问题的常用方法是 : 先证其中两条直线交于一点 , 再证其他直线经过该点 . - 19 - 考点一 考点二 考点三 对点训练 1 (1) 如图 , α ∩ β =l , A , B ∈ α , C ∈ β , 且 C ∉ l , 直线 AB ∩ l=M , 过 A , B , C 三点的平面记作 γ , 则 γ 与 β 的交线必通过 ( 　　 ) A. 点 A B. 点 B C. 点 C 但不过点 M D. 点 C 和点 M (2) 以下四个命题中 : ① 不共面的四点中 , 其中任意三点不共线 ; ② 若点 A , B , C , D 共面 , 点 A , B , C , E 共面 , 则点 A , B , C , D , E 共面 ; ③ 若直线 a , b 共面 , 直线 a , c 共面 , 则直线 b , c 共面 ; ④ 依次首尾相接的四条线段必共面 . 正确命题的个数是 ( 　　 ) A.0 B.1 C.2 D.3 D B - 20 - 考点一 考点二 考点三 解析 : (1) ∵ A , B ∈ γ , M ∈ AB , ∴ M ∈ γ . 又 α ∩ β =l , M ∈ l , ∴ M ∈ β . 根据公理 3 可知 , M 在 γ 与 β 的交线上 . 同理可知 , 点 C 也在 γ 与 β 的交线上 . (2) ① 正确 , 否则三点共线和第四点必共面 ; ② 错 , 如图三棱锥 , 能符合题意 , 但 A , B , C , D , E 不共面 ; 从 ② 的几何体知 , ③ 错 ; 由空间四边形可知 , ④ 错 . - 21 - 考点一 考点二 考点三 空间两条直线的位置关系 ( 多考向 ) 考向 1 　 两直线位置关系的判定 例 2 a , b , c 为三条不重合的直线 , 已知下列结论 : ① 若 a ⊥ b , a ⊥ c , 则 b ∥ c ; ② 若 a ⊥ b , a ⊥ c , 则 b ⊥ c ; ③ 若 a ∥ b , b ⊥ c , 则 a ⊥ c. 其中正确的个数为 ( 　　 ) A.0 B.1 C.2 D.3 B 解析 : 方法一 : 在空间中 , 若 a ⊥ b , a ⊥ c , 则 b , c 可能平行 , 也可能相交 , 还可能异面 , 所以 ①② 错误 , ③ 显然成立 . 方法二 : 构造长方体或正方体模型可快速判断 , ①② 错误 , ③ 正确 . 思考 如何比较直观地判断两直线的位置关系 ? - 22 - 考点一 考点二 考点三 考向 2 　 异面直线的判定 例 3 如图所示 , 正方体 ABCD-A 1 B 1 C 1 D 1 中 , M , N 分别为棱 C 1 D 1 , C 1 C 的中点 , 有以下四个结论 : ① 直线 AM 与 CC 1 是相交直线 ; ② 直线 AM 与 BN 是平行直线 ; ③ 直线 BN 与 MB 1 是异面直线 ; ④ 直线 AM 与 DD 1 是异面直线 . 其中正确的结论为 　　　　 ( 把你认为正确的结论序号都填上 ) .   ③④ 解析 : 因为点 A 在平面 CDD 1 C 1 外 , 点 M 在平面 CDD 1 C 1 内 , 直线 CC 1 在平面 CDD 1 C 1 内 , CC 1 不过点 M , 所以 AM 与 CC 1 是异面直线 , 故 ① 错 ; 取 DD 1 中点 E , 连接 AE , 则 BN ∥ AE , 但 AE 与 AM 相交 , 故 ② 错 ; 因为点 B 1 与直线 BN 都在平面 BCC 1 B 1 内 , 点 M 在平面 BCC 1 B 1 外 , BN 不过点 B 1 , 所以 BN 与 MB 1 是异面直线 , 故 ③ 正确 ; 同理 ④ 正确 . 故填 ③④ . - 23 - 考点一 考点二 考点三 思考 空间两条直线位置关系的判定方法有哪些 ? - 24 - 考点一 考点二 考点三 考向 3 　 异面直线所成的角 例 4 (2017 全国 Ⅱ , 理 10) 已知直三棱柱 ABC-A 1 B 1 C 1 中 , ∠ ABC= 120 ° , AB= 2, BC=CC 1 = 1, 则异面直线 AB 1 与 BC 1 所成角的余弦值为 ( 　　 ) C 解析 : 方法一 : 如图 , 取 AB , BB 1 , B 1 C 1 的中点 M , N , P , 连接 MN , NP , PM , 可知 AB 1 与 BC 1 所成的角等于 MN 与 NP 所成的角 . - 25 - 考点一 考点二 考点三 - 26 - 考点一 考点二 考点三 思考 求异面直线所成角的方法有哪些 ? - 27 - 考点一 考点二 考点三 解题心得 1 . 点、线、面之间的位置关系可借助正方体为模型 , 以正方体为主线直观感知并认识空间点、线、面的位置关系 , 准确判定线线平行、线线垂直、线面平行、线面垂直、面面平行、面面垂直 . 2 . 空间两条直线位置关系的判定方法 - 28 - 考点一 考点二 考点三 3 . 求解异面直线所成角的方法 - 29 - 考点一 考点二 考点三 对点训练 2 (1) 若直线 l 1 和 l 2 是异面直线 , l 1 在平面 α 内 , l 2 在平面 β 内 , l 是平面 α 与平面 β 的交线 , 则下列命题正确的是 ( 　　 ) A. l 与 l 1 , l 2 都不相交 B. l 与 l 1 , l 2 都相交 C. l 至多与 l 1 , l 2 中的一条相交 D. l 至少与 l 1 , l 2 中的一条相交 (2) 若空间中四条两两不同的直线 l 1 , l 2 , l 3 , l 4 , 满足 l 1 ⊥ l 2 , l 2 ⊥ l 3 , l 3 ⊥ l 4 , 则下列结论一定正确的是 ( 　　 ) A. l 1 ⊥ l 4 B. l 1 ∥ l 4 C. l 1 与 l 4 既不垂直也不平行 D. l 1 与 l 4 的位置关系不确定 D D - 30 - 考点一 考点二 考点三 (3) 在图中 , G , N , M , H 分别是正三棱柱的顶点或所在棱的中点 , 则表示直线 GH , MN 是异面直线的图形有 　　　　　 . ( 填上所有正确答案的序号 )   ②④ - 31 - 考点一 考点二 考点三 (4)(2017 四川成都三诊 , 文 8) 在我国古代数学名著《九章算术》中 , 将四个面都为直角三角形的四面体称为鳖臑 , 如图 , 在鳖臑 ABCD 中 , AB ⊥ 平面 BCD , 且 AB=BC=CD , 则异面直线 AC 与 BD 所成角的余弦值为 ( 　　 ) A - 32 - 考点一 考点二 考点三 解析 : (1) l 1 与 l 在平面 α 内 , l 2 与 l 在平面 β 内 , 若 l 1 , l 2 与 l 都不相交 , 则 l 1 ∥ l , l 2 ∥ l , 根据直线平行的传递性 , 则 l 1 ∥ l 2 , 与已知矛盾 , 故 l 至少与 l 1 , l 2 中的一条相交 . (2) 构造如图所示的正方体 ABCD-A 1 B 1 C 1 D 1 , 取 l 1 为 AD , l 2 为 AA 1 , l 3 为 A 1 B 1 , 当取 l 4 为 B 1 C 1 时 , l 1 ∥ l 4 , 当取 l 4 为 BB 1 时 , l 1 ⊥ l 4 , 故排除 A,B,C, 选 D . - 33 - 考点一 考点二 考点三 (3) 图 ① 中 , 直线 GH ∥ MN ; 图 ② 中 , G , H , N 三点共面 , 但 M ∉ 平面 GHN , 因此直线 GH 与 MN 异面 ; 图 ③ 中 , 连接 GM , 则 GM ∥ HN , 因此 GH 与 MN 共面 ; 图 ④ 中 , G , M , N 共面 , 但 H ∉ 平面 GMN , 因此 GH 与 MN 异面 . 所以在图 ②④ 中 , GH 与 MN 异面 . (4) 如图所示 , 分别取 AB , AD , BC , BD 的中点 E , F , G , O , 则 EF ∥ BD , EG ∥ AC , FO ⊥ OG , ∴ ∠ FEG 为异面直线 AC 与 BD 所成角 . - 34 - 考点一 考点二 考点三 空间中线面的位置关系 例 5 设直线 m 与平面 α 相交但不垂直 , 则下列说法正确的是 ( 　　 ) A. 在平面 α 内有且只有一条直线与直线 m 垂直 B. 过直线 m 有且只有一个平面与平面 α 垂直 C. 与直线 m 垂直的直线不可能与平面 α 平行 D. 与直线 m 平行的平面不可能与平面 α 垂直 B - 35 - 考点一 考点二 考点三 解析 : 如图 , m 是平面 α 的斜线 , PA ⊥ α , l ⊂ α , l ⊥ AB , 则 l ⊥ m , 平面 α 内所有与 l 平行的直线都垂直于 m , 故 A 错 ; 由题意可知过 m 有且只有一个平面 PAB 与平面 α 垂直 , 假设有两个平面都与平面 α 垂直 , 则这两个平面的交线 m 应与平面 α 垂直 , 与条件矛盾 , 故 B 正确 ; 又 l' ⊄ α , l' ∥ l , ∴ l' ∥ α , ∵ l ⊥ m , ∴ l' ⊥ m , 故 C 错 ; 又在平面 α 内取不在直线 AB 上的一点 D , 过 D 可作平面 β 与平面 PAB 平行 , ∴ m ∥ β , ∵ 平面 PAB ⊥ α , ∴ 平面 β ⊥ α , 故 D 错 . - 36 - 考点一 考点二 考点三 思考 如何借助空间图形确定线面位置关系 ? 解题心得 解决这类问题的关键就是熟悉直线与直线、直线与平面、平面与平面的各种位置关系及相应的公理定理 , 归纳整理平面几何中成立但立体几何中不成立的命题 , 并在解题过程中注意避免掉入由此设下的陷阱 . 判断时可由易到难进行 , 一般是作图分析 , 构造出符合题设条件的图形或反例来判断 . - 37 - 考点一 考点二 考点三 对点训练 3 已知正方体 ABCD-A 1 B 1 C 1 D 1 , 点 P , Q , R 分别是线段 B 1 B , AB 和 A 1 C 上的动点 , 观察直线 CP 与 D 1 Q , CP 与 D 1 R , 给出下列结论 : ① 对于任意给定的点 P , 存在点 Q , 使得 D 1 Q ⊥ CP ; ② 对于任意给定的点 Q , 存在点 P , 使得 CP ⊥ D 1 Q ; ③ 对于任意给定的点 P , 存在点 R , 使得 D 1 R ⊥ CP ; ④ 对于任意给定的点 R , 存在点 P , 使得 CP ⊥ D 1 R. 其中正确的结论是 　　　　　 . ( 填序号 ) ②③ - 38 - 考点一 考点二 考点三 解析 : ① 当点 P 与 B 重合时 , DD 1 ⊥ CP , 若 D 1 Q ⊥ CP , 又 DD 1 ∩ D 1 Q=D 1 , 则 CP ⊥ 平面 DD 1 Q , CP ⊥ DQ , 此时 , 在 AB 上不存在点 Q 使 CP ⊥ DQ , 所以 ① 错误 ; ② 当点 P 与 B 1 重合时 , CP ⊥ AB , 且 CP ⊥ AD 1 , 所以 CP ⊥ 平面 ABD 1 . 因为对于任意给定的点 Q , 都有 D 1 Q ⊂ 平面 ABD 1 , 所以对于任意给定的点 Q , 存在点 P , 使得 CP ⊥ D 1 Q , 所以 ② 正确 ; ③ 只有 CP 垂直 D 1 R 在平面 BCC 1 B 1 中的射影时 , D 1 R ⊥ CP , 所以 ③ 正确 ; ④ 当点 R 与 A 1 重合时 , D 1 R ∥ B 1 C 1 , 若 D 1 R ⊥ CP , 则 B 1 C 1 ⊥ CP , 此时在 BB 1 上不存在点 P 使 B 1 C 1 ⊥ CP , 所以 ④ 错误 . - 39 - 考点一 考点二 考点三 1 . 公理 1 是判断一条直线是否在某个平面内的依据 ; 公理 2 及其推论是判断或证明点、线共面的依据 ; 公理 3 是证明三线共点或三点共线的依据 . 要能够熟练用文字语言、符号语言、图形语言来表示公理 . 2 . 判定空间两条直线是异面直线的方法 (1) 判定定理 : 平面外一点 A 与平面内一点 B 的连线和平面内不经过点 B 的直线是异面直线 . (2) 反证法 : 证明两线不可能平行、相交或证明两线不可能共面 , 从而可得两线异面 . - 40 - 考点一 考点二 考点三 1 . 异面直线易误解为 “ 分别在两个不同平面内的两条直线为异面直线 ”, 实质上两异面直线不能确定任何一个平面 , 因此异面直线既不平行 , 也不相交 . 2 . 直线与平面的位置关系在判断时最易忽视 “ 线在面内 ” .