- 846.00 KB
- 2021-04-13 发布
云天化中学2016—2017学年度下学期阶段测试(二)
高二年级 数学试卷(理科)
第I卷(选择题,共分)
一、 选择题:本大题共小题,每小题分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,集合,则( )
A. B. C. D.
2. 定义运算=ad-bc,则符合条件=0的复数z的共轭复数在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若椭圆的离心率为,则双曲线的渐近线方程为( )
A. B. C. D.
4.已知函数,若=-1,则实数a的值为( )
A.2 B.±1 C.1 D.一1
5.“0≤m≤l”是“函数有零点”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
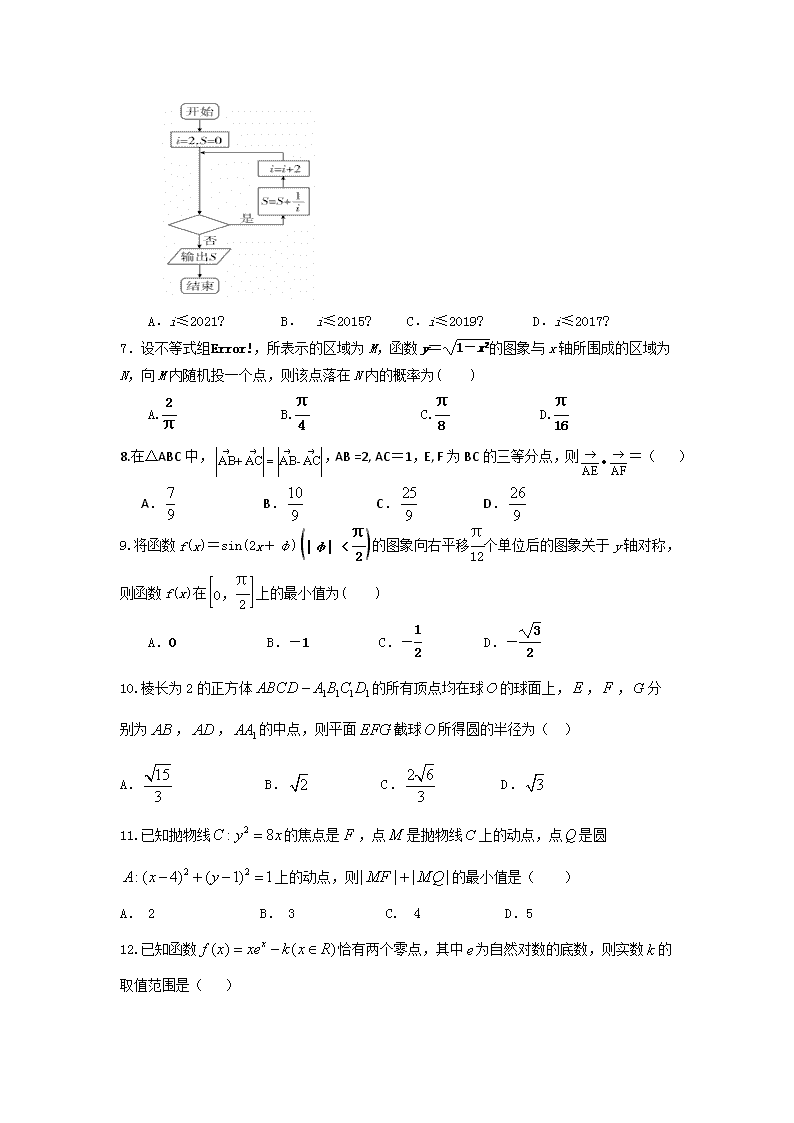
6. 如图,给出的是计算+++…+的值的程序框图,其中判断框内应填入的是( )
A.i≤2021? B. i≤2015? C.i≤2019? D.i≤2017?
7.设不等式组,所表示的区域为M,函数y=的图象与x轴所围成的区域为N,向M内随机投一个点,则该点落在N内的概率为( )
A. B. C. D.
8.在△ABC中,,AB =2, AC=1,E, F为BC的三等分点,则=( )
A. B. C. D.
9.将函数f(x)=sin(2x+φ)的图象向右平移个单位后的图象关于y轴对称,则函数f(x)在上的最小值为( )
A.0 B.-1 C.- D.-
10.棱长为2的正方体的所有顶点均在球的球面上,,,分别为,,的中点,则平面截球所得圆的半径为( )
A. B. C. D.
11.已知抛物线的焦点是,点是抛物线上的动点,点是圆上的动点,则的最小值是( )
A. 2 B. 3 C. 4 D.5
12.已知函数恰有两个零点,其中为自然对数的底数,则实数的取值范围是( )
A. B. C. D.
第Ⅱ卷 客观题(共分)
一、 填空题(每小题分,小题共分)
13设函数若,则的值为_____ ;
14. 设Sn为等比数列{an}的前n项和,a2-8a5=0,则的值为 ;
15. 某几何体的三视图如图所示,则该几何体的体积是 ;
16.已知函数满足,且,当时,,那么在区间内,关于的方程且恰有4个不同的根,则的取值范围是 .
三、解答题(第题分,其余每题分,共分,解答应写出证明过程或演算步骤)
17.(本题10分)
在△ABC中,角A,B,C的对边分别为a,b,c。已知a=1,A=,。
(I)求B,C的值;
(II)求△ABC的面积.
18. (本题12分)
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在[30,50)和[130,150]的学生中共抽取6人,该6人中成绩在[130,150]的有几人?
(3)在(2)中抽取的6人中,随机抽取2人,求分数在[30,50)和[130,150]各1人的概率.
19. (本题12分)
若数列满足为常数),则称数列为调和数列.
(1)已知数列调和数列,且满足求的通项公式;
(2)若数列为调和数列,且,求的前项和.
20. (本题12分)
如图,在三棱锥A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
(Ⅰ)证明:DQ∥平面CPM;
(Ⅱ)若二面角C﹣AB﹣D的大小为,求∠BDC的正切值.
21. (本题12分)
已知椭圆的焦点在轴上,离心率等于,且过点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右焦点作直线交椭圆于两点,交轴于点,若,求证:为定值.
22. (本题12分)
已知函数
(1)若函数的最小值为0,求的值;
(2)证明:.
云天化中学2016—2017学年度下学期阶段测试(二)
高二数学(理科) 参考答案
附参考答案:
一、选择题(本大题共12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
A
C
A
D
B
B
D
A
D
C
【解析】
1.,,,故选C.
2.由题意得,2zi-[-i(1+i)]=0,则z==--,∴=-+,其在复平面内对应的点在第二象限,故选B.
3.椭圆的离心率为,可得,可得,解得,∴双曲线的渐近线方程为:,故选A.
4.,故选C.
5.,由,得,且,所以函数有零点.反之,函数有零点,只需 ,故选A.
6. 判断框内可填“i≤2016?”或“i≤2017?”或“i<2017?”或“i<2018?”选D.
7.本题考查不等式组表示的平面区域、几何概型.在平面直角坐标系内画出题中的不等式组表示的平面区域为以(,0),(-,0),(0,)为顶点的三角形区域,函数y=的图象与x轴围成的区域如图中的阴影部分所示,则所求概率为=,故选B.
8.由知,以所在直线分别为x轴、y轴建立平面直角坐标系,则,于是,据此,,故选B.
9. f(x)=sin(2x+φ)的图象向右平移个单位后得到g(x)=sin=sin的图象,又g(x)的图象关于y轴对称,
∴g(0)=sin=±1,
∴-+φ=+kπ(k∈Z),
∴φ=+kπ(k∈Z),又|φ|<,
∴φ=-,∴f(x)=sin,又x∈,
∴2x-∈,∴f(x)min=-.故选D。
10.如图2,正方体的外接球球心O为对角线的中点,球半径,球心O到平面的距离为,所以小圆半径,故选A.
11.解析:抛物线的准线是,作于,由抛物线的定义知,所以要使最小,即最小,只要,,三点共线且在与之间即可,此时的最小值是:,选D.
12.解析:函数有两个零点,可转化为函数与恰有两个交点,因为,当时,,单调递减;当时,,单调递增,在处取得极小值;而当时,恒成立,
利用图像可知,选.
二、填空题:
13.解:
14.解:设{an}的公比为q,依题意得==q3,因此q=.注意到a5+a6+a7+a8=q4(a1+a2+a3+a4),即有S8-S4=q4S4,因此S8=(q4+1)S4,=q4+1=,
15.本题考查几何体的三视图和体积.由三视图得该几何体为底面半径为1,高为2的圆柱体挖去一个底面边长为的正方形,高为1的正四棱锥后剩余的部分,则其体积为2×π×12-×()2×1=2π-,
16.令,则化为,即直线恒过.根据题意,画出的图象与直线,如图所示,由图象可知当直线介于直线与之间时,关于x的方程(且)恰有4个不同的根,又因为,,所以.
三、解答题
17.解:(Ⅰ),
,
,
,
又.
又,. ………………………………(6分)
(Ⅱ)由,得,
.………………………(10分)
18.解:(1)由频率分布直方图,得该校高三学生本次数学考试的平均分为:
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100+0.0125×20×120+0.0025×20×140=92.…(4分)
(2)样本中分数在[30,50)和[130,150]的人数分别为6人和3人,
所以抽取的6人中分数在[130,150]的人有(人)…(8分)
(3)由(2)知:抽取的6人中分数在[30,50)的有4人,记为A1,A2,A3,A4
分数在[130,150]的人有2人,记B1,B2,
从中随机抽取2人总的情形有:
(A1,A2)、(A1,A3)、(A1,A4)、(A1,B1)、(A1,B2)、(A2,A3)、
(A2,A4)、(A2,B1)、(A2,B2)、(A3,A4)、(A3,B1)、(A3,B2)、
(A4,B1)、(A4,B2)、(B1,B2)15种;
而分数在[30,50)和[130,150]各1人的情形有(A1,B1)、(A1,B2)、(A2,B1)、
(A2,B2)、(A3,B1)、(A3,B2)、(A4,B1)、(A4,B2)8种
故分数在[30,50)和[130,150]各1人的概率…(12分)
19.解:(Ⅰ)因为为调和数列,故为等差数列,
又, ……………………(2分)
故是以1为首项,1为公差的等差数列,
故,
故. ………………………………(5分)
(Ⅱ)为调和数列,故.
由知道,,
故是以1为首项,2为公差的等差数列, ……………………………(7分)
故,, ……(9分)
. ………………………………(12分)
20.解:(Ⅰ)取AB的中点E,则,所以EQ∥PC.
又EQ⊄平面CPM,所以EQ∥平面CPM. …
又PM是△BDE的中位线,所以DE∥PM,
从而DE∥平面CPM.…
所以平面DEQ∥平面CPM,…
故DQ∥平面CPM. …(5分)
(Ⅱ)解法1:由AD⊥平面BCD知,AD⊥CM
由BC=CD,BM=MD,知BD⊥CM,
故CM⊥平面ABD. …
由(Ⅰ)知DE∥PM,而DE⊥AB,故PM⊥AB.
所以∠CPM是二面角C﹣AB﹣D的平面角,
即. …
设PM=a,则,,
在Rt△CMD中,. …
所以∠BDC的正切值为.…(12分)
解法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系.
设MC=a,MD=b,则C(a,0,0),B(0,﹣b,0),A(0,b,2b)…
则,
设平面ABC的一个法向量,
则即取…
平面ABD的一个法向量为,…
所以,所以
在Rt△CMD中,
所以∠BDC的正切值为. …(12分)
21.(本小题满分12分)
(Ⅰ)解:设椭圆C的方程为,
,,
∴椭圆C的标准方程为. ………………………………………………(4分)
(Ⅱ)证明:设点A,B,M的坐标分别为,
又易知F点的坐标为.
显然直线l存在斜率,设直线l的斜率为k,
则直线l的方程是,
将直线l的方程代入到椭圆C的方程中,消去y并整理得
, ……………………………………………(8分)
, ……………………………………………(9分)
又,
将各点坐标代入得, …………………………………(11分)
. ………………………………………………(12分)
22.(本小题满分12分)
解 (1)f(x)=ln x+-1的定义域为(0,+∞),
且f′(x)=-=.
若a≤0,则f′(x)>0,于是f(x)在(0,+∞)上单调递增,
故f(x)无最小值,不符合题意.
若a>0,则当0a时,f′(x)>0.
故f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.
于是当x=a时,f(x)取得最小值ln a.
由已知得ln a=0,解得a=1.
综上,a=1. (6分)
(2)证明:①下面先证当x∈(0,π)时,ex+(ln x-1)sinx>0.
因为x∈(0,π),所以只要证>1-ln x.
由(1)可知≥1-ln x,
于是只要证>,即只要证xex-sinx>0.
令h(x)=xex-sinx,则h′(x)=(x+1)ex-cosx.
当01·e0-1=0,
所以h(x)在(0,π)上单调递增.
所以当0h(0)=0,即xex-sinx>0.
故当x∈(0,π)时,不等式ex+(ln x-1)sinx>0成立.
②当x∈[π,+∞)时,由(1)知≥1-ln x,
于是有x≥1-ln,即x≥1+ln x.
所以ex≥e1+ln x,即ex≥ex,
又因为ex≥e(1+ln x),所以ex≥e(1+ln x),
所以ex+(ln x-1)sinx≥e(ln x+1)+(ln x-1)sinx
=(e+sinx)ln x+(e-sinx)>0.
综上,不等式ex+(ln x-1)sinx>0成立.(12分)