2020届中考数学全程演练 第二部分 图形与几何 第十一单元 解直角三角形 第34课时 锐角三角函数 7页

第十一单元 解直角三角形 第34课时 锐角三角函数 ‎(60分)‎ 一、选择题(每题3分，共21分)‎ ‎1．[2017·杭州]在直角三角形ABC中，已知∠C＝90°，∠A＝40°，BC＝3，则AC＝ (D)‎ A．3sin40° B．3sin50° C．3tan40° D．3tan50°‎ 图34－1‎ ‎2．[2016·山西]如图34－1，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是 (D)‎ A．2 B. C. D. ‎【解析】　如答图，连结AC，由勾股定理，得AC＝，AB＝2，BC＝，AB2＋AC2＝BC2，AC⊥AB.‎ 第2题答图 则tan∠B＝＝.‎ 图34－2‎ ‎3．[2016·丽水]如图34－2，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是 (C)‎ A. B. C. D. ‎4．[2017·汕尾]在Rt△ABC中，∠C＝90°，若sinA＝，则cosB的值是(B)‎ A. B. C. D. 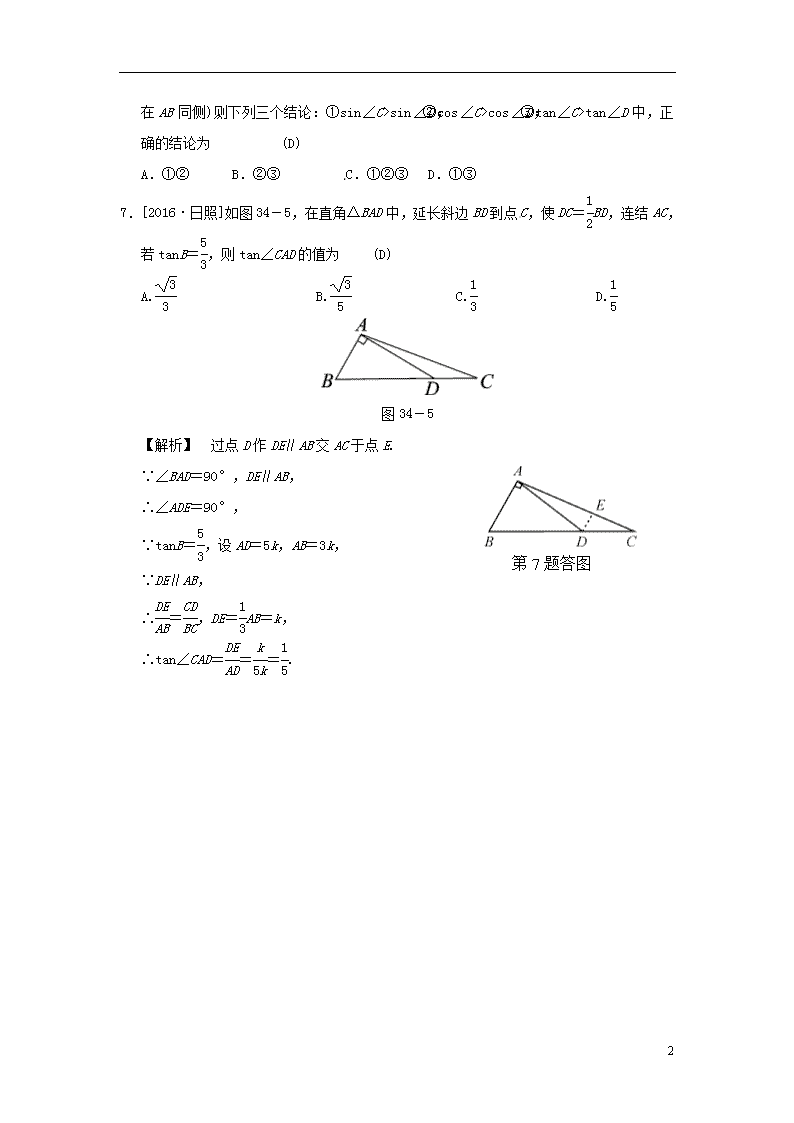图34－3‎ ‎5．[2017·湖州]如图34－3，已知在Rt△ABC中，∠C＝90°，AC＝4，tanA＝，则BC的长是 (A)‎ A．2 B．‎3 ‎ C．4 D．8‎ 图34－4‎ ‎6．[2016·扬州]如图34－4，若锐角△ABC内接于⊙O，点D在⊙O外(与点C 7‎ 在AB同侧)，则下列三个结论：①sin∠C>sin∠D；②cos∠C>cos∠D；③tan∠C>tan∠D中，正确的结论为 (D)‎ A．①② B．②③ C．①②③ D．①③‎ ‎7．[2016·日照]如图34－5，在直角△BAD中，延长斜边BD到点C，使DC＝BD，连结AC，若tanB＝，则tan∠CAD的值为 (D)‎ A. B. C. D. 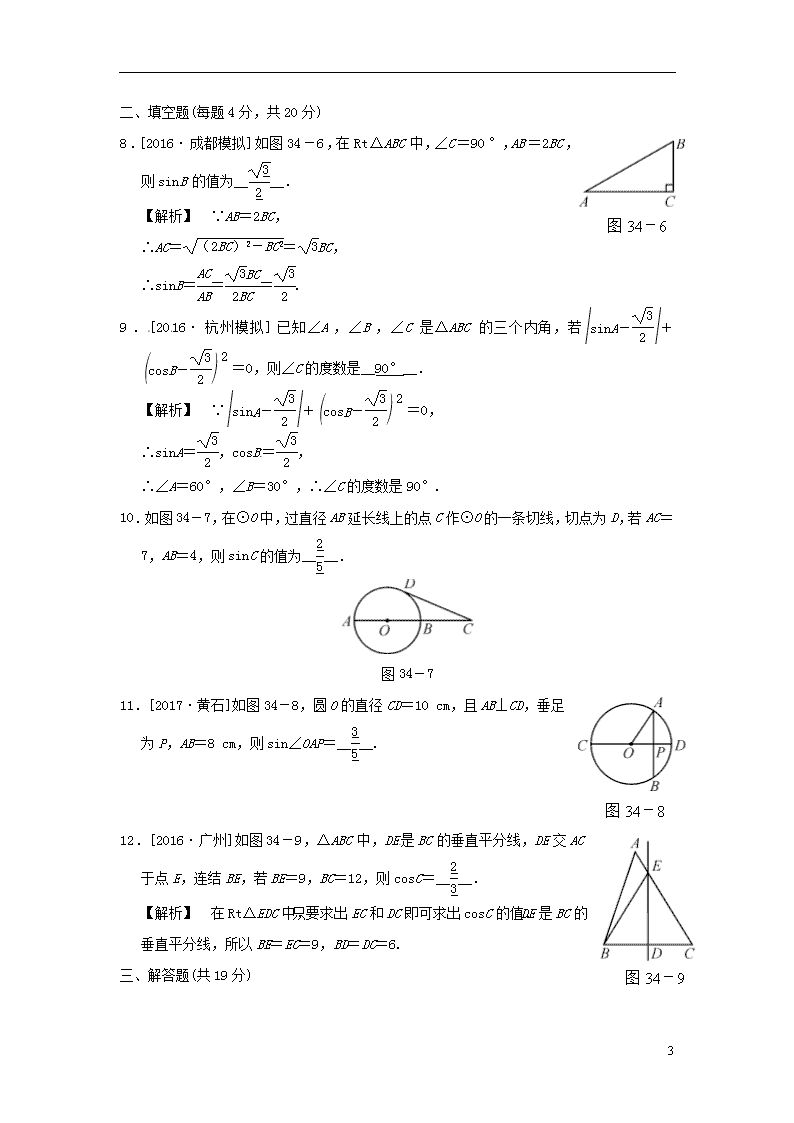图34－5‎ ‎【解析】　过点D作DE∥AB交AC于点E.‎ 第7题答图 ‎∵∠BAD＝90°，DE∥AB，‎ ‎∴∠ADE＝90°，‎ ‎∵tanB＝，设AD＝5k，AB＝3k，‎ ‎∵DE∥AB，‎ ‎∴＝，DE＝AB＝k，‎ ‎∴tan∠CAD＝＝＝.‎ 7‎ 二、填空题(每题4分，共20分)‎ 图34－6‎ ‎8．[2016·成都模拟]如图34－6，在Rt△ABC中，∠C＝90°，AB＝2BC，则sinB的值为____．‎ ‎【解析】　∵AB＝2BC，‎ ‎∴AC＝＝BC，‎ ‎∴sinB＝＝＝.‎ ‎9．[2016·杭州模拟]已知∠A，∠B，∠C是△ABC的三个内角，若＋＝0，则∠C的度数是__90°__．‎ ‎【解析】　∵＋＝0，‎ ‎∴sinA＝，cosB＝，‎ ‎∴∠A＝60°，∠B＝30°，∴∠C的度数是90°.‎ ‎10．如图34－7，在⊙O中，过直径AB延长线上的点C作⊙O的一条切线，切点为D，若AC＝7，AB＝4，则sinC的值为____．‎ 图34－7‎ 图34－8‎ ‎11．[2017·黄石]如图34－8，圆O的直径CD＝‎10 cm，且AB⊥CD，垂足为P，AB＝‎8 cm，则sin∠OAP＝____.‎ 图34－9‎ ‎12．[2016·广州]如图34－9，△ABC中，DE是BC的垂直平分线，DE交AC于点E，连结BE，若BE＝9，BC＝12，则cosC＝____．‎ ‎【解析】　在Rt△EDC中，只要求出EC和DC即可求出cosC的值．DE是BC的垂直平分线，所以BE＝EC＝9，BD＝DC＝6.‎ 三、解答题(共19分)‎ 7‎ ‎13．(9分)如图34－10，在Rt△ABC中，∠C＝90°，AB＝10，sinA＝，求BC的长和tanB的值．‎ 图34－10‎ 解：∵sinA＝＝，‎ 又∵AB＝10，∴BC＝4.‎ 又∵AC＝＝2，‎ ‎∴tanB＝＝.‎ ‎14．(10分)计算：‎ ‎(1)[2016·永州]cos30°－＋；‎ ‎(2)[2016·绵阳]＋－＋.‎ 解：(1)原式＝－＋22‎ ‎＝－＋4‎ ‎＝4；‎ ‎(2)原式＝－(1－)＋－＋ ‎＝－1＋－＋(－2)‎ ‎＝－1＋4－－2＝1.‎ ‎(28分)‎ ‎15．(8分)[2017·重庆]如图34－11，△ABC中，AD⊥BC，垂足是D，若BC＝14，AD＝12，tan∠BAD＝，求sinC的值．‎ 7‎ 图34－11‎ 解：∵AD⊥BC，‎ ‎∴tan∠BAD＝，‎ ‎∵tan∠BAD＝，AD＝12，‎ ‎∴BD＝9，‎ ‎∴CD＝BC－BD＝14－9＝5，‎ ‎∴在Rt△ADC中，AC＝＝＝13，‎ ‎∴sinC＝＝.‎ ‎16．(10分)[2016·酒泉]如图34－12①，将直尺摆放在三角板上，使直尺与三角板的边分别交于点D，E，F，G，已知∠CGD＝42°.‎ 图34－12‎ ‎(1)求∠CEF的度数；‎ ‎(2)将直尺向下平移，使直尺的边缘通过三角板的顶点B，交AC边于点H，如图②所示，点H，B在直尺上的度数分别为4，13.4，求BC的长(结果保留两位小数)．‎ ‎(参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90)‎ 解：(1)∵∠CGD＝42°，∠C＝90°，‎ ‎∴∠CDG＝90°－42°＝48°，‎ ‎∵DG∥EF，∴∠CEF＝∠CDG＝48°；‎ ‎(2)∵点H，B的读数分别为4，13.4，‎ ‎∴HB＝13.4－4＝9.4，‎ ‎∴BC＝HB·cos42°≈9.4×0.74≈6.96.‎ 7‎ ‎∴BC的长为6.96.‎ 图34－13‎ ‎17．(10分)[2017·长沙]如图34－13，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O.‎ ‎(1)求证：△AOE≌COD；‎ ‎(2)若∠OCD＝30°，AB＝，求△AOC的面积．‎ 解：(1)证明：由折叠的性质可得：AE＝AB，∠E＝∠B＝90°，‎ ‎∵四边形ABCD是矩形，‎ ‎∴CD＝AB，∠D＝90°，‎ ‎∴AE＝CD，∠E＝∠D＝90°，‎ 又∵∠AOE＝∠COD，‎ ‎∴△AOE≌△COD(AAS)；‎ ‎(2)∵∠OCD＝30°，AB＝＝CD，‎ ‎∴OD＝CD·tan∠OCD＝·tan30°＝×＝1，OC＝2，‎ 由折叠知∠BCA＝∠ACO，‎ ‎∵AD∥BC，∴∠OAC＝∠BCA，‎ ‎∴∠OAC＝∠ACO，∴OA＝OC＝2，‎ ‎∴S△AOC＝·OA·CD＝×2×＝.‎ ‎(12分)‎ ‎18．(12分)[2017·遂宁]如图34－14，根据图中数据完成填空，再按要求答题：‎ 图34－14‎ ‎(1)sin‎2A1＋sin2B1＝__1__；sin‎2A2＋sin2B2＝__1__；sin‎2A3＋sin2B3＝__1__；‎ ‎(2)观察上述等式，猜想：在Rt△ABC中，∠C＝90°.都有：sin‎2A＋sin2B＝__1__；‎ ‎④‎ ‎(3)如图④，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别是a，b，c；利用三角函数的定义和勾股定理，证明你的猜想；‎ 7‎ ‎ (4)已知：∠A＋∠B＝90°，且sinA＝，求sinB.‎ 解：(3)证明：∵sinA＝，sinB＝，a2＋b2＝c2，‎ sin‎2A＋sin2B＝＋＝＝1；‎ ‎(4)∵sinA＝，sin‎2A＋sin2B＝1，‎ ‎∴sinB＝＝.‎ 7‎