2017-2018学年福建省永春县第一中学高二下学期期末考试数学（文）试题（Word版） 12页

‎2017-2018学年福建省永春县第一中学高二下学期期末考试（文）数学科试卷（2018.07）‎ 命题：张隆亿 时间：120分钟 满分：150分 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．若命题：，则为(　　)‎ A． B． ‎ C． D． ‎ ‎2．已知集合，，则(　　)‎ A． B． C． D．‎ ‎3．若复数满足是虚数单位，则复数的共轭复数 (　　)‎ A． B． C． D．‎ ‎4．为了得到函数的图象，只需把函数的图象上的所有的点(　　)‎ A．向左平移1个单位长度，再向下平移1个单位长度 B．向右平移1个单位长度，再向下平移1个单位长度 C．向左平移1个单位长度，再向上平移1个单位长度 D．向右平移1个单位长度，再向上平移1个单位长度 ‎5．若函数为偶函数，则等于(　　)‎ A．－2 B．－1 C．1 D．2‎ ‎6．已知函数在区间上的图象是连续的曲线，若在区间上是增函数，‎ 则(　　)‎ A．在上一定有零点 B．在上一定没有零点 C．在上至少有一个零点 D．在上至多有一个零点 ‎7．已知定义在上的奇函数，当时，恒有，且当时，‎ ‎，则(　　)‎ A．0 B． C． D．‎ ‎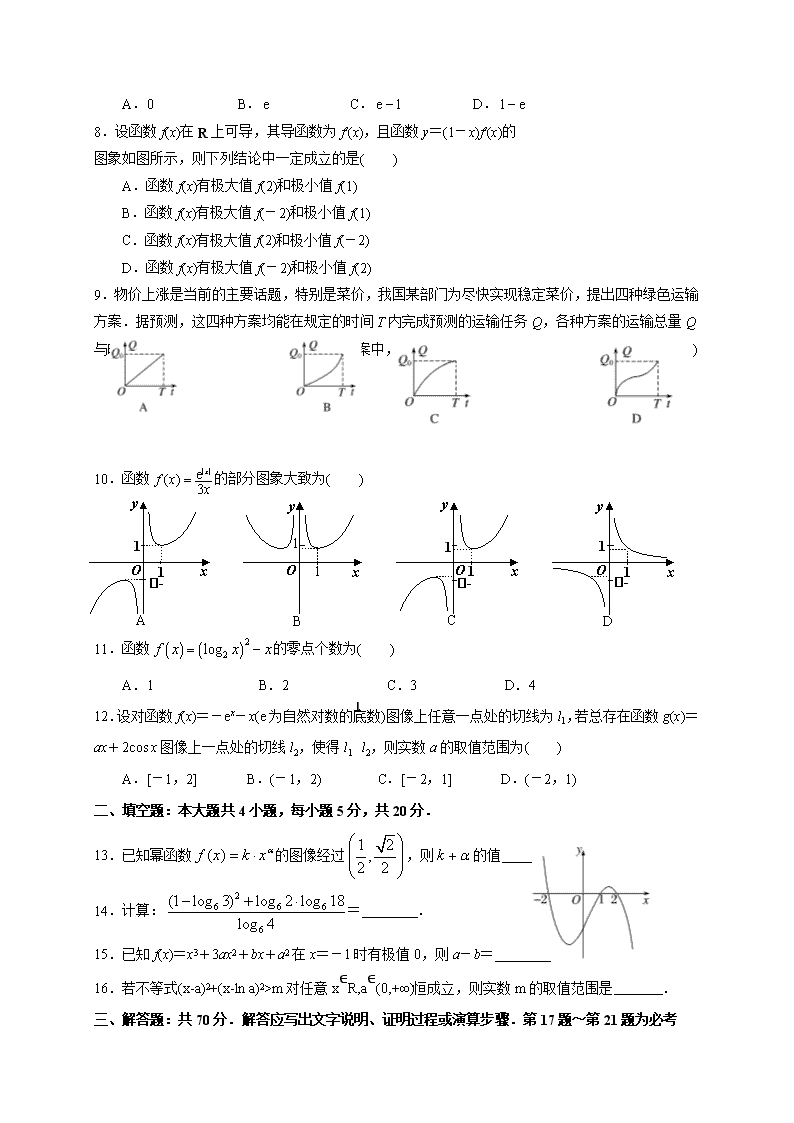8．设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的 图象如图所示，则下列结论中一定成立的是(　　)‎ A．函数f(x)有极大值f(2)和极小值f(1)‎ B．函数f(x)有极大值f(－2)和极小值f(1)‎ C．函数f(x)有极大值f(2)和极小值f(－2)‎ D．函数f(x)有极大值f(－2)和极小值f(2)‎ ‎9．物价上涨是当前的主要话题，特别是菜价，我国某部门为尽快实现稳定菜价，提出四种绿色运输方案．据预测，这四种方案均能在规定的时间T内完成预测的运输任务Q，各种方案的运输总量Q与时间t的函数关系如图所示，在这四种方案中，运输效率(单位时间的运输量)逐步提高的是(　　)‎ B ‎1‎ ‎1‎ O x y --1‎ ‎1‎ ‎1‎ O D x y ‎1‎ ‎1‎ O A x y --1‎ ‎1‎ ‎1‎ O C x y --1‎ ‎10．函数的部分图象大致为(　　)‎ ‎11．函数的零点个数为(　　)‎ A．1　　　　 B．2　　　 　C．3　　 　 　D．4‎ ‎12．设对函数f(x)＝－ex－x(e为自然对数的底数)图像上任意一点处的切线为l1，若总存在函数g(x)＝ax＋2cos x图像上一点处的切线l2，使得l1⊥l2，则实数a的取值范围为(　　)‎ A．[－1，2] B．(－1，2) C．[－2，1] D．(－2，1) ‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．已知幂函数的图像经过，则的值 ．‎ ‎14．计算：＝ ．‎ ‎15．已知f(x)＝x3＋3ax2＋bx＋a2在x＝－1时有极值0，则a－b＝________．‎ ‎16．若不等式(x-a)2+(x-ln a)2>m对任意x∈R,a∈(0,+∞)恒成立，则实数m的取值范围是 ．‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17题～第21题为必考 题，每个试题考生都必须做答.第22、23题为选考题，考生根据要求做答．‎ ‎（一）必考题（共60分）‎ ‎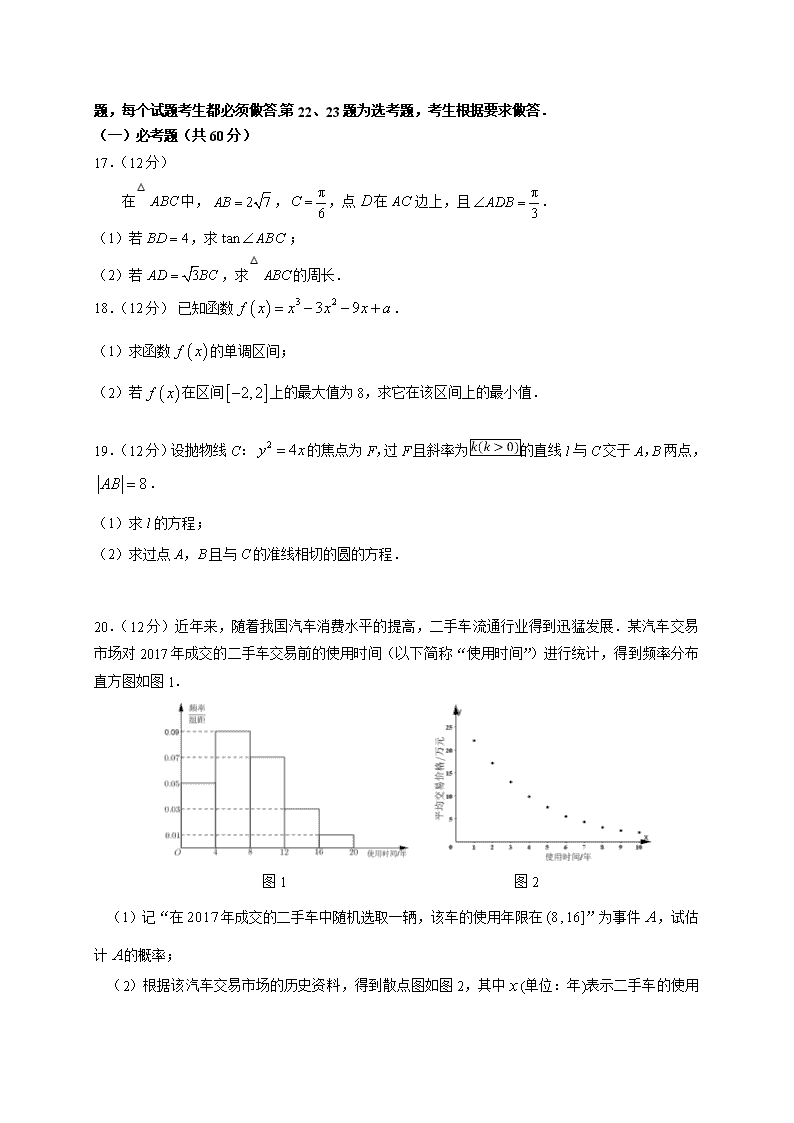17．（12分）‎ 在△中，，，点在边上，且．‎ ‎（1）若，求；‎ ‎（2）若，求△的周长．‎ ‎18．（12分） 已知函数．‎ ‎（1）求函数的单调区间；‎ ‎（2）若在区间上的最大值为8，求它在该区间上的最小值．‎ 19． ‎（12分）设抛物线C：的焦点为F，过F且斜率为的直线l与C交于A，B两点，．‎ ‎（1）求l的方程；‎ ‎（2）求过点A，B且与C的准线相切的圆的方程．‎ ‎20．（12分）近年来，随着我国汽车消费水平的提高，二手车流通行业得到迅猛发展．某汽车交易市场对2017年成交的二手车交易前的使用时间（以下简称“使用时间”）进行统计，得到频率分布直方图如图1． ‎ ‎ ‎ 图1 图2‎ ‎（1）记“在年成交的二手车中随机选取一辆，该车的使用年限在”为事件，试估计的概率；‎ ‎（2）根据该汽车交易市场的历史资料，得到散点图如图2，其中 ‎(单位：年)表示二手车的使用时间，(单位：万元)表示相应的二手车的平均交易价格．‎ 由散点图看出，可采用作为二手车平均交易价格关于其使用年限的回归方程，相关数据如下表（表中，）： ‎ ‎5.5‎ ‎8.7‎ ‎1.9‎ ‎301.4‎ ‎79.75‎ ‎385‎ ‎①根据回归方程类型及表中数据，建立关于的回归方程；‎ ‎②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格的佣金，对使用时间8年以上(不含8年)的二手车收取成交价格的佣金．在图1对使用时间的分组中，以各组的区间中点值代表该组的各个值．若以2017年的数据作为决策依据，计算该汽车交易市场对成交的每辆车收取的平均佣金．‎ 附注：①对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为；‎ ‎②参考数据：．‎ ‎21．（12分）已知函数． ‎（1）求曲线在点(0,－1)处的切线方程；‎ ‎（2）证明：当时，．‎ 选考题：共10分．请考生在（22）、（23）两题中任选一题作答．如果多做，则按所做第一题计分．‎ ‎22．选修4－4：坐标系与参数方程（10分）‎ 在平面直角坐标系中，直线的参数方程为为参数．在以原点为极点，轴正半轴为极轴的极坐标系中，曲线的极坐标方程为．‎ ‎（1）求直线的极坐标方程和曲线的直角坐标方程；‎ ‎（2）设与交于两点，求．‎ ‎23．选修4－5：不等式选讲（10分）‎ 已知函数，，．‎ ‎（1）当时，解关于的不等式；‎ ‎（2）若对任意，都存在，使得不等式成立，求实数的取值范围．‎ 永春一中高二年（文）期末考数学参考答案和评分细则 评分说明：‎ ‎1. 本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要 考查内容比照评分标准制定相应的评分细则。‎ ‎2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分。 ‎ ‎3．解答右端所注分数，表示考生正确做到这一步应得的累加分数。‎ ‎4．只给整数分数。选择题和填空题不给中间分。‎ 一、选择题：本大题共12小题，每小题5分，共60分。‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C D A C D D D B C C A 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎13． 14． 1 15．－7 16．(-∞,)‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。‎ ‎17．解法一：如图，已知，，‎ 所以，则.………………1分 在△中，根据余弦定理，，‎ 所以. 2分 ‎（1）在△中，，，，‎ 由余弦定理，‎ 所以，解得，所以，‎ 在△中，由正弦定理，‎ 所以，， 4分 由，，，在△中，由，得 ‎ ‎，故， 5分 所以 ，‎ 所以 7分 ‎（2）设，则，从而，‎ 故． 9分 在△中，由余弦定理得，‎ 因为 ，所以，解得． 11分 所以．故△周长为． 12分 解法二：如图，已知，，所以，则. …… 1分 在△中，根据余弦定理，，‎ 所以. 2分 ‎（1）在△中，，，，‎ 由余弦定理，‎ 所以，解得， 3分 由余弦定理， ‎ 又因为，所以．‎ 所以， 5分 所以． 7分 ‎（2）同解法一． 12分 ‎18．解析：(1)由题知： 2分 令则x<-1或x>3; 令则-10）． 1分 设A（x1，y1），B（x2，y2）．‎ 由得． 3分 ‎△=，故． 5分 所以．‎ 由题设知，解得k=–1（舍去），k=1． 6分 因此l的方程为y=x–1． 7分 ‎（2）由（1）得AB的中点坐标为（3，2），所以AB的垂直平分线方程为 ‎，即． 8分 设所求圆的圆心坐标为（x0，y0），则 解得或 10分 因此所求圆的方程为或． 12分 ‎20．解：（1）由频率分布直方图得，该汽车交易市场2017年成交的二手车使用时间在的频率为，在的频率为 3分 所以． 4分 ‎（2）①由得，即关于的线性回归方程为． 5分 因为，‎ ‎[]‎ 所以关于的线性回归方程为， 7分 即关于的回归方程为 8分 ‎②根据①中的回归方程和图1，对成交的二手车可预测：‎ 使用时间在的平均成交价格为，对应的频率为；‎ 使用时间在的平均成交价格为，对应的频率为；‎ 使用时间在的平均成交价格为，对应的频率为；‎ 使用时间在的平均成交价格为，对应的频率为；‎ 使用时间在的平均成交价格为，对应的频率为 所以该汽车交易市场对于成交的每辆车可获得的平均佣金为 万元 12分 ‎21．解：（1）， 2分 ‎． 3分 因此曲线在点(0,-1)处的切线方程是． 4分 ‎（2）当时，． 6分 ‎ 3分 令，则． 8分 ‎∵在R上单调递增，且 ‎∴当时，，单调递减；当时，，单调递增； 10分 所以． 11分 故． 12分 ‎22．解法一：（1）由得的普通方程为， 1分 又因为， 所以的极坐标方程为． 3分 由得，即， 4分 所以的直角坐标方程为． 5分 ‎（2）设的极坐标分别为，则 6分 由消去得， 7分 化为，即， 8分 因为，即，所以，或， 9分 即或所以． 10分 解法2： （1）同解法一 5分 ‎（2）曲线的方程可化为，表示圆心为且半径为1的圆． 6分 将的参数方程化为标准形式(其中为参数)，代入的直角坐标方程为得，，‎ 整理得，，解得或． 8分 设对应的参数分别为 ，则．所以， 9分 又因为是圆上的点，所以 10分 解法3： （1）同解法一 5分 ‎（2）曲线的方程可化为，表示圆心为且半径为1的圆． 6分 又由①得的普通方程为， 7分 则点到直线的距离为， 8分 所以，所以是等边三角形，所以， 9分 又因为是圆上的点，所以 10分 ‎23．解：（1）当时，，则 2分 当时，由得，，解得； ‎ 当时，恒成立；‎ 当时，由得，，解得． 4分 所以的解集为． 5分 ‎（2）因为对任意，都存在，使得不等式成立，‎ 所以． 6分 因为，所以，‎ 且，…①‎ 当时，①式等号成立，即． 7分 又因为，…②‎ 当时，②式等号成立，即． 8分 所以，整理得，， 9分 解得或，即的取值范围为． 10分