北师大版八年级数学 上册 第五章五节 同步课时练习题（附参考答案） 29页

北师八上数学测试题第五章五节 ‎1.如图5-7-1,l甲,l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象,并回答下列问题.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　图5-7-1‎ ‎(1)乙出发时,与甲相距　　　　　　km; ‎ ‎(2)走了一段路程后,乙的自行车发生故障,停下来修理,修车的时间为　　　　　　h; ‎ ‎(3)乙从出发起,经过　　　　　　h与甲相遇; ‎ ‎(4)甲行走的路程s(km)与时间t(h)之间的函数关系是　　　　　　　　; ‎ ‎(5)如果乙的自行车不出现故障,那么乙出发后经过　　　　h与甲相遇,相遇处离乙的出发点　　　km.‎ ‎2.如图5-7-2,直线l1和l2的交点坐标为(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图5-7-2‎ A.(4,-2)‎ B.(2,-4)‎ C.(-4,2)‎ D.(3,-1)‎ ‎3.如图5-7-3,l1,l2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(小时)的函数图象,假设两种灯泡的使用寿命都是2 000小时,照明效果一样.‎ ‎(1)l1的函数关系式为　　　　　　　　　　;l2的函数关系式为　　　　　　　　　　.‎ ‎(2)当照明时间为　　　　　　小时,两种灯的费用相等.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　图5-7-3‎ ‎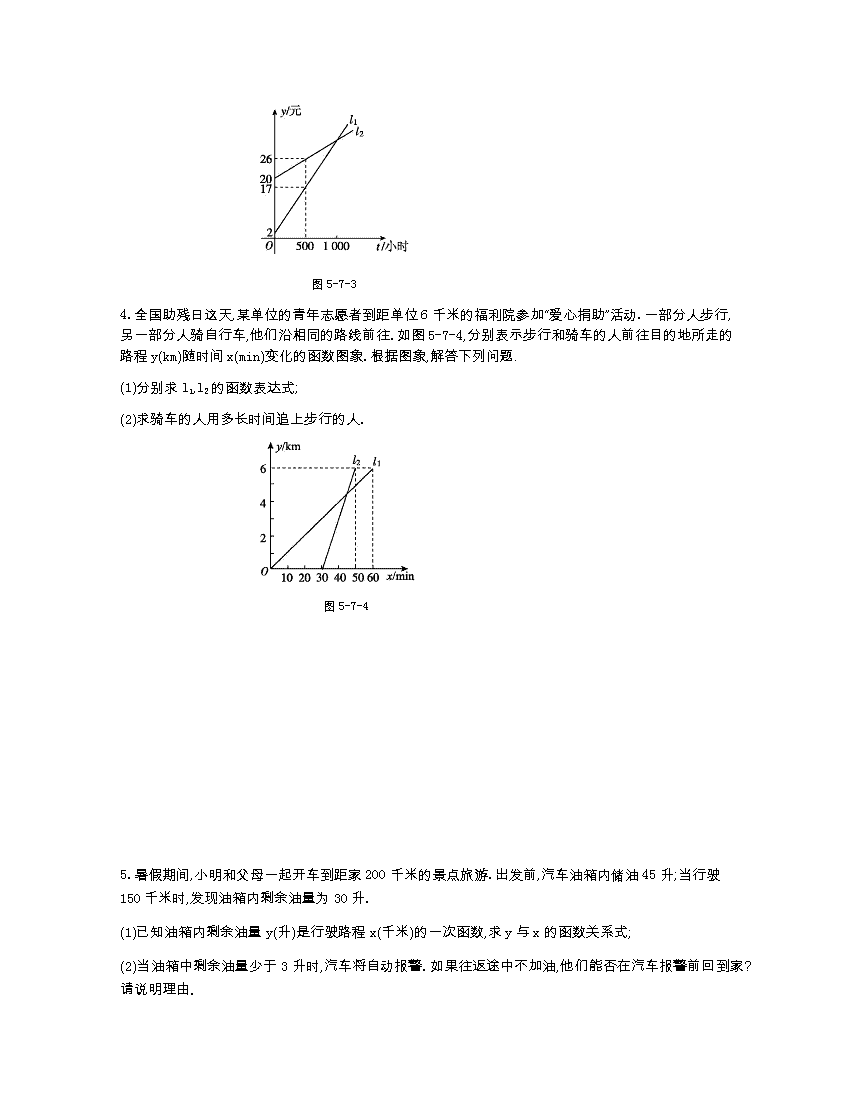4.全国助残日这天,某单位的青年志愿者到距单位6千米的福利院参加“爱心捐助”活动.一部分人步行,另一部分人骑自行车,他们沿相同的路线前往.如图5-7-4,分别表示步行和骑车的人前往目的地所走的路程y(km)随时间x(min)变化的函数图象.根据图象,解答下列问题.‎ ‎(1)分别求l1,l2的函数表达式;‎ ‎(2)求骑车的人用多长时间追上步行的人.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　图5-7-4‎ ‎5.暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱内剩余油量为30升.‎ ‎(1)已知油箱内剩余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;‎ ‎(2)当油箱中剩余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.‎ ‎6.A地向B地打国际长途电话,设通话时间为x(分),需付电话费y(元),通话3分以内话费为3.6元.根据如图5-7-5所示的y随x变化的图象,可得通话8分钟需付电话费　　　　　　元.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图5-7-5‎ ‎7.已知一次函数图象经过点(3,-3),并与直线y=4x-3相交于x轴上一点,求此函数的表达式.‎ ‎8.如图5-7-6,直线l1,l2的交点坐标可以看成一个方程组的解,则这个方程组是(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图5-7-6‎ A.‎ B.‎ C.‎ D.‎ ‎9.某自来水公司为了鼓励市民节约用水,采取分段收费标准,若某用户居民每月应缴水费y(元)是用水量x(立方米)的函数,其图象如图5-7-7所示,根据图象,回答下列问题.‎ ‎(1)分别求出0≤x≤5和x>5时,y与x的函数关系式.‎ ‎(2)自来水公司的收费标准是什么?‎ ‎(3)若某户居民缴水费50元,该月用水多少立方米?‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　　图5-7-7‎ ‎10.小颖和小亮上山游玩,小颖乘缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m /min,设小亮出发x min后行走的路程为y m,图5-7-8中的折线表示小亮在整个行走过程中y与x的函数关系.‎ ‎(1)当50≤x≤80时,求y与x的函数关系式;‎ ‎(2)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图5-7-8‎ ‎11.图5-7-9是某工程队在“村村通”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象.根据图象提供的信息,可知该公路的长度是　　　　　　米.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图5-7-9‎ ‎12.如图5-7-10所示,直线l1的表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.‎ ‎(1)求点D的坐标;‎ ‎(2)求直线l2的表达式;‎ ‎(3)求△ADC的面积.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　图5-7-10‎ ‎13.星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.注完之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图5-7-11所示.‎ ‎(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气?‎ ‎(2)当x≥0.5时,求储气罐中的储气量y(m3)与时间x(h)的函数表达式;‎ ‎(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图5-7-11‎ ‎14.如果(a-1)x+5yb+1+2z|a|=10是一个三元一次方程,那么a=　　　　　　,b=　　　　　　.‎ ‎15.下列方程组中,为三元一次方程组的是(　　)‎ A.‎ B.‎ C.‎ D.‎ ‎16.三元一次方程x+2y+z=5的解有(　　)‎ A.1个 B.2个 C.3个 D.无数个 ‎17.下面四组数中,是方程组的解的是(　　)‎ A.‎ B.‎ C.‎ D.‎ ‎18.解下列三元一次方程组.‎ ‎(1)‎ ‎(2)‎ ‎(3)‎ ‎ (4)‎ ‎ (5)‎ ‎19.甲、乙、丙三个数的和是35,甲数的2倍比乙数大5,乙数的等于丙数的.求这三个数.‎ ‎20.解三元一次方程组时,为把它转化为二元一次方程组,最简便的方法(　　)‎ A.由②③消去未知数z B.由②③消去未知数y C.由①②消去未知数x D.由①③消去未知数x ‎21.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需31.5元;若购铅笔4支,练习本8本,圆珠笔2支共需42元,那么,购铅笔、练习本、圆珠笔各1件共需(　　)‎ A. 12元 B. 10.5元 C. 9.5元 D. 9元 ‎22.已知x+2y+3z=12,6x+5y+4z=16,则x+y+z的值为(　　)‎ A.3‎ B.4‎ C.5‎ D.不确定 ‎23.在方程5x+y-2z=1中,若x=1,y=-2,则z=　　　　　　.‎ ‎24.已知三元一次方程组则x+y+z=　　　　　.‎ ‎25.如果方程组的解使等式kx+2y-z=10成立,那么k的值为　　　　　　.‎ ‎26.若|x-1|+(2y+1)2+(3z+2)2=0,则2x-y+z=　　　　　　.‎ ‎27.解下列三元一次方程组.‎ ‎(1)‎ ‎ (2)‎ ‎ (3)‎ ‎ (4)‎ ‎(5)‎ ‎28.某单位职工在植树节时去植树,甲、乙、丙三个小组共植树50株,乙组植树的株数是甲、丙两组的和的,甲组植树的株数恰是乙组与丙组的和,问每组各植树多少株?‎ ‎29.下列四组数值中,方程组的解的是(　　)‎ A.‎ B.‎ C.‎ D.‎ ‎30.解下列三元一次方程组.‎ ‎(1)‎ ‎ (2) = = =2‎ ‎ (3)‎ ‎31.在等式y=ax2+bx+c中,当x=1时,y=0;当x=2时,y=3;当x=-3时,y=28.求a,b,c的值.‎ ‎32.汛期来临,某乡防汛指挥部紧急购进草袋、编织袋、麻袋共5 000条,共支出2 700元.已知三种袋子的单价依次是0.3元、0.75元和1.5元,又知买草袋与编织袋所花的钱数相等,求三种袋子各购进多少条.‎ ‎33.某种食品由油、糖、面三种主要成分混合加工而成,如果这三种成分重量的比依次为1:2:5,那么要加工这种食品1 000千克,需要油、糖、面各多少千克?‎ ‎34.有1元、5元、10元的人民币共30张,合计178元,其中5元的比1元的多2张,三种人民币各有多少张?‎ ‎35.某汽车在相距70千米的A,B两地往返行驶,从A地到B地,依次分别是一段平路,一段上坡路,一段下坡路.已知该汽车从A地到B地需要2小时30分钟,而从B地返回A地则只需2小时18分钟.若汽车在平地上行驶的速度为每小时30千米,上坡的速度为每小时20千米,下坡的速度为每小时40千米,问从A地到B地,平路、上坡路、下坡路各是多少千米?‎ ‎36.某农场有300人耕种51公顷土地,计划种植水稻、棉花和蔬菜,各种农作物每公顷所需的劳动力人数和所需要投入的资金如下表.‎ 如果该农场计划投入资金67万元,那么应如何安排这3种农作物的种植面积,才能使所有人都有工作,并且使计划投入资金正好够用?‎ 农作物品种 每公顷所需劳动力 每公顷所需投入资金 水稻 ‎4人 ‎1万元 棉花 ‎8人 ‎1万元 蔬菜 ‎5人 ‎2万元 回答问题.‎ 参考答案 ‎1.(1)10‎ ‎(2)1‎ ‎(3)2.5‎ ‎(4)s=5t+10(t≥0)‎ ‎(5)1　　　15‎ ‎2.A ‎3.(1)y=0.03x+2　　　y=0.012x+20‎ ‎(2)1000‎ ‎4.解:(1)设l1的表达式为y1=k1x.由图象知l1过点(60,6),所以60k1=6,即k1=.所以y1=x(0≤x≤60).‎ 设l2的表达式为y2=k2x+b.‎ 由图象知l2经过(30,0)和(50,6)两点,‎ 所以 解得 所以y2=x-9(30≤x≤50).‎ ‎(2)当骑车的人追上步行的人时,y1=y2,即 = x-9,所以x=45.‎ 又45-30=15(min),所以骑车的人用15 min追上步行的人.‎ ‎5.解:(1)设y=kx+b.‎ 依题意,得 解得 所以函数关系式为y=-x+45.‎ ‎(2)当x=400时,y=-×400+45=5>3,‎ 所以他们能在汽车报警前回到家 ‎6.9.6‎ ‎7.解:因为直线y=4x-3与x轴的交点坐标是 (,0),一次函数的图象与直线y=4x-3交于x轴上一点,‎ 所以此一次函数图象与直线y=4x-3的交点是(,0).‎ 设此一次函数的表达式为y=kx+b.①‎ 将(3,-3)和(,0)分别代入①,‎ 得 解得 所以此函数的表达式为y=-x+1.‎ ‎8.A ‎9.解:(1)y=‎ ‎(2)每月不超过5立方米,则每立方米水收取4元;若超过5立方米,则超出部分每立方米收取6元.‎ ‎(3)10立方米.‎ ‎10.解:(1)当50≤x≤80时,设y与x的函数关系式为y=kx+b.‎ 根据题意,当x=50时,y=1950;‎ 当x=80时,y=3600.‎ 所以 解得 所以当50≤x≤80时,y与x的函数关系式为y=55x-800.‎ ‎(2)缆车到山顶的路线长为3600÷2=1800(m),‎ 缆车到达终点所需时间为1800÷180=10(min),‎ 小颖到达终点时,小亮行走的时间为10+50=60(min),‎ 把x=60代入y=55x-800,得y=55×60-800=2500.‎ 所以当小颖到达缆车终点时,小亮离缆车终点的路程是3600-2500=1100(m).‎ ‎11.504‎ ‎12.解:(1)由y=-3x+3,令y=0,得-3x+3=0.所以x=1.所以D(1,0).‎ ‎(2)设直线l2的表达式为y=kx+b.由图象知,直线l2过点A(4,0)和点B(3,-),‎ 所以 解得 所以直线l2的表达式为y=x-6.‎ ‎(3)由 解得 所以C(2,-3).‎ 因为AD=3,所以S△ADC=×3×|-3|=.‎ ‎13.解:(1)由图可知,星期天当日注入了10000-2000=8000(m3)的天然气.‎ ‎(2)当x≥0.5时,设储气罐中的储气量y(m3)与时间x(h)的函数表达式为y=kx+b(k,b为常数,且k≠0),‎ 因为它的图象过点(0.5,10000),(10.5,8000),‎ 所以 解得 所以,当x≥0.5时,储气罐中的储气量y(m3)与时间x(h)的函数表达式为y=-200x+10 100(x≥0.5).‎ ‎(3)可以.因为给18辆车加气需18×20=360(立方米),储气量为10 000-360=9 640(立方米),‎ 于是有9 640=-200x+10 100,解得x=2.3.‎ 而从8:00到10:30相差2.5小时,‎ 显然有2.3<2.5,‎ 故第18辆车在当天10:30之前可以加完气.‎ ‎14.-1　　　0‎ ‎15.C ‎16.D ‎17.B ‎18.(1)解:①+②,得5x+2y=16.　　④‎ ‎③+②,得3x+4y=18.　　⑤‎ 由④⑤得方程组 解得 代入③,得2+3+z=6.‎ 解得z=1.‎ 所以原方程组的解为 ‎(2)解:由①×3+③,得7x+y=15.　④‎ ‎②与④组成二元一次方程组 解这个二元一次方程组,得 把x=2代入①,得z=3.‎ 所以原方程组的解为 ‎(3)解:由③+①,得 ‎3x+5y=11.　④‎ 由③×2+②,得 ‎3x+3y=9.　⑤‎ 由④-⑤,得2y=2,y=1.‎ 将y=1代入⑤,得 ‎3x=6,x=2.‎ 将x=2,y=1代入①,得 z=6-2×2-3×1=-1.‎ 所以原方程组的解为 ‎(4)解:由①-②,得 x-z=-2.　④‎ ‎③与④组成二元一次方程组 解这个二元一次方程组,得 把x=代入①,得y=.‎ 所以原方程组的解为 ‎(5)解:由①-②,得3y=3.‎ 解得y=1.‎ 把y=1代入①,得 x+z=1.　④‎ 把y=1代入③,得 x+3z=-3.　⑤‎ ‎④与⑤组成二元一次方程组 解这个二元一次方程组,得 所以原方程组的解为 ‎19.解:设甲数为x,乙数为y,丙数为z.‎ 由题意可得方程组:‎ 解得 所以甲数为10,乙数为15,丙数为10.‎ ‎20.B ‎21.B ‎22.B ‎23.1‎ ‎24.3‎ ‎25.‎ ‎26.‎ ‎27.(1)解:由①×2-②,得 ‎-y-3z=0.④‎ 由①-③,得3y=-15.‎ 解得y=-5.‎ 将y=-5代入方程④,得z=.‎ 把y,z的值代入①,得x-5-=5.‎ 解得x=.‎ 所以原方程组的解为 ‎(2)解:①+②,得2y=16.‎ 解这个方程,得y=8.‎ ‎①+③,得2x=12.‎ 解这个方程,得x=6.‎ 把x=6,y=8代入①,得z=3.‎ 所以原方程组的解为 ‎(3)解:①-③,得y=-3.‎ 把y=-3代入②,得z=5.‎ 把z=5代入①,得x=1.‎ 所以原方程组的解为 ‎(4)解:将原方程组改写为 由方程②,得x=6+4y.‎ 代入①化简,得 ‎11y-4z=-19.④‎ 由③得2y+3z=4.⑤‎ 由④×3+⑤×4,得33y+8y=-57+16.‎ 解得y=-1.‎ 将y=-1代入⑤,得z=2.‎ 将y=-1代入②,得x=2.‎ 所以原方程组的解为 ‎(5)解:由①-②,得3y=3.‎ 解得y=1.‎ 将y=1分别代入②③,得 解得 所以原方程组的解为 ‎28.解:设甲组植树x株,乙组植树y株,丙组植树z株.‎ 由题意,得,‎ 解得 答:甲组植树25株,乙组植树10株,丙组植树15株.‎ ‎29.D ‎30.(1)解:由①变形,得y=x.　④‎ 由②变形,得z=x.　⑤‎ 把④与⑤代入③,得2x-x=34.‎ 解这个方程,得x=35.‎ 把x=35代入④,得y=21.‎ 把x=35代入⑤,得z=15.‎ 所以原方程组的解为 ‎(2)解:原方程组可化为 由②,得y=3.‎ 把y=3代入③,得 ‎5x-z=9.　④‎ ‎①与④组成二元一次方程组 解这个二元一次方程组,得 所以原方程组的解为 ‎(3)解:又①-②,得 x-y=0.　④‎ 由③×2-②×3,得 ‎4x+y=20.　⑤‎ ‎④与⑤组成二元一次方程组 解这个二元一次方程组,得 把x=4,y=4代入①,得z=-3.‎ 所以原方程组的解为 ‎31.解:根据题意得 解得 故a,b,c的值分别为2,-3,1.‎ ‎32.解:设购进草袋x条,编织袋y条,麻袋z条.‎ 根据题意,得 解得 答:购进草袋3 200条,编织袋1 280条,麻袋520条.‎ ‎33.解:设需要油x千克,糖y千克,面z千克.‎ 根据题意,得 解得 答:需要油125千克,糖250千克,面625千克.‎ ‎34.解:设1元的人民币有x张,5元的有y张,10元的有z张.‎ 根据题意,得 解得 答:1元的人民币有8张,5元的有10张,10元的有12张.‎ ‎35.解:设从A地到B地,平路为x千米,上坡路为y千米,下坡路为z千米.‎ 根据题意,得 解得 答:从A地到B地,平路为54千米,上坡路为12千米,下坡路为4千米.‎ ‎36.解:设种植水稻x公顷,棉花y公顷,蔬菜z公顷.‎ 根据题意,得 解得 答:种植水稻15公顷,棉花20公顷,蔬菜16公顷.‎