2018-2019学年湖北省宜昌市协作体高一上学期期末考试数学试题（解析版） 14页

‎2018-2019学年湖北省宜昌市协作体高一上学期期末考试数学试题 一、单选题 ‎1．已知集合，，则（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】利用集合交集的概念，求得两个集合的公共元素，也即两个集合的交集.‎ ‎【详解】‎ 根据集合交集的概念可知，，故选B.‎ ‎【点睛】‎ 本小题主要考查考查集合交集的概念及运算，属于基础题.‎ ‎2．的值是 ( )‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由于==.‎ 故选A．‎ ‎3．已知关于的不等式，则该不等式的解集为（ ）‎ A．［4，+∞) B．(-4，+∞) C．(-∞,-4 ) D．‎ ‎【答案】B ‎【解析】现将不等式两边化为同底，然后利用指数函数单调性列一元一次不等式，由此求得不等式的解集.‎ ‎【详解】‎ 依题意可知，原不等式可转化为，由于指数函数为增函数，故，故选B.‎ ‎【点睛】‎ 本小题主要考查指数运算，考查指数函数的单调性以及指数不等式的解法，属于基础题.‎ ‎4．函数的周期，振幅，初相分别是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】利用求得周期，直接得出振幅为，在中令求得初相.‎ ‎【详解】‎ 依题意，，函数的振幅为，在中令求得初相为.故选C.‎ ‎【点睛】‎ 本小题主要考查中所表示的含义，考查三角函数周期的计算.属于基础题.其中表示的是振幅，是用来求周期的，即，要注意分母是含有绝对值的.称为相位，其中称为初相.还需要知道的量是频率，也即是频率是周期的倒数.‎ ‎5．已知向量a=(3，1)，b=(2k－1，k），a⊥b，则k的值是（ ）‎ A．－1 B． C．－ D．‎ ‎【答案】B ‎【解析】根据两个向量垂直的坐标表示列方程，解方程求得的值.‎ ‎【详解】‎ 由于两个向量垂直，故，，故选B.‎ ‎【点睛】‎ 本小题主要考查两个平面向量垂直的坐标表示，考查方程的思想，属于基础题.‎ ‎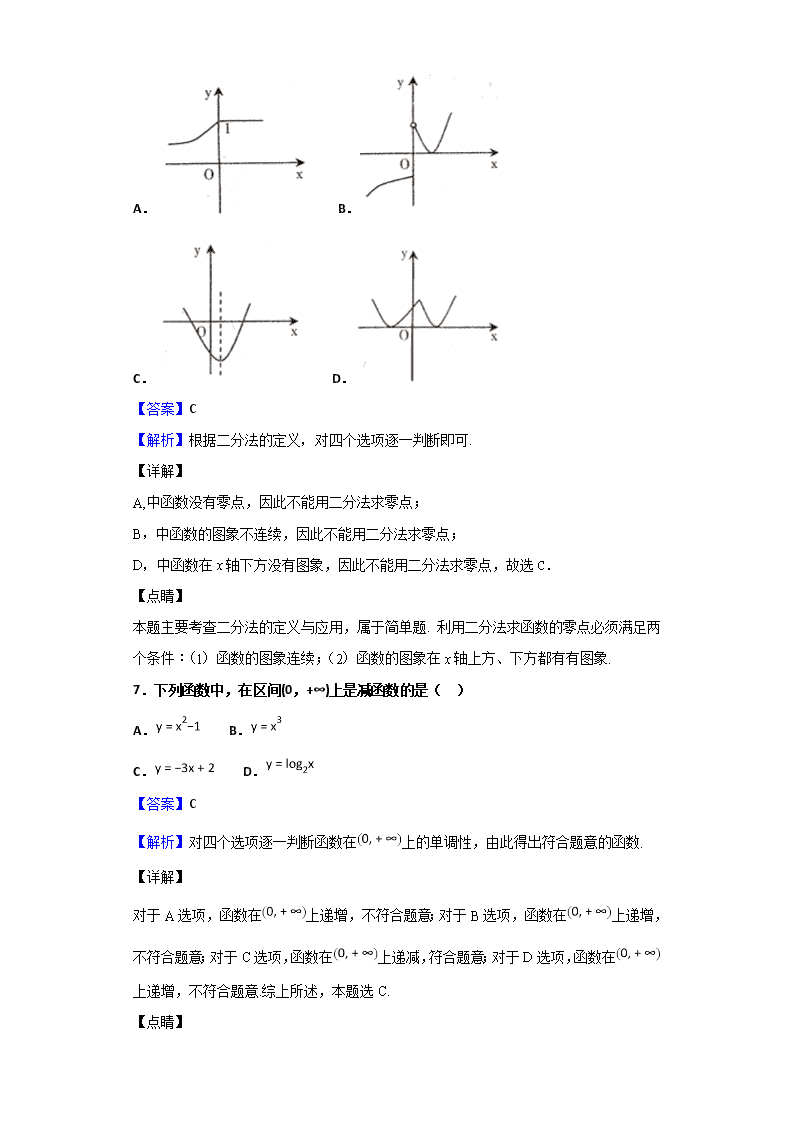6．下列图像表示的函数能用二分法求零点的是（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】根据二分法的定义，对四个选项逐一判断即可.‎ ‎【详解】‎ A,中函数没有零点，因此不能用二分法求零点；‎ B，中函数的图象不连续，因此不能用二分法求零点；‎ D，中函数在x轴下方没有图象，因此不能用二分法求零点，故选C．‎ ‎【点睛】‎ 本题主要考查二分法的定义与应用，属于简单题. 利用二分法求函数的零点必须满足两个条件：（1）函数的图象连续；（2）函数的图象在x轴上方、下方都有有图象.‎ ‎7．下列函数中，在区间(0，+∞)上是减函数的是（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】对四个选项逐一判断函数在上的单调性，由此得出符合题意的函数.‎ ‎【详解】‎ 对于A选项，函数在上递增，不符合题意；对于B选项，函数在上递增，不符合题意；对于C选项，函数在上递减，符合题意；对于D选项，函数在上递增，不符合题意.综上所述，本题选C.‎ ‎【点睛】‎ 本小题主要考查基本初等函数的单调性，属于基础题.其中二次函数的单调性由和对称轴共同决定，时，函数图像开口向上，在对称轴两边左减右增.时，函数图像开口向下，在对称轴两边左增右减.一次函数的单调性由来决定，当时递增，当时递减.‎ ‎8．已知，，，则（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】试题分析：由指数函数，对数函数的性质，可知，‎ ‎，即，选A ‎【考点】指数函数，对数函数的性质 ‎9．函数的图象的一部分如图所示，则、的值分别为（ ）‎ A．1， B．1，‎ C．2， D．2，‎ ‎【答案】D ‎【解析】由f（0）=sinφ=，|φ|＜可以求得φ，又ω?+φ=π，可求ω的值．‎ 解：∵f（x）=sin（ωx+φ），‎ ‎∴f（0）=sinφ，又f（0）=，‎ ‎∴sinφ=，又|φ|＜，‎ ‎∴φ=；‎ 又ω?+φ=π，即ω?+=π，‎ ‎∴ω=2．‎ 故答案为D．‎ ‎10．要得到函数y=sin(2x+)的图像,只需把函数y=sin2x的图像（ ）‎ A．向左平移个单位 B．向左平移个单位 C．向右平移个单位 D．向右平移个单位 ‎【答案】B ‎【解析】将目标函数变为，由此求得如何将变为目标函数.‎ ‎【详解】‎ 依题意，目标函数可转化为，故只需将向左平移个单位，故选B.‎ ‎【点睛】‎ 本小题主要考查三角函数图像变换中的平移变换，属于基础题.‎ ‎11．某同学从家里赶往学校，一开始乘公共汽车匀速前进，在离学校还有少许路程时，改为步行匀速前进到校．下列图形纵轴表示该同学与学校的距离s，横轴表示该同学出发后的时间t，则比较符合该同学行进实际的是（ ）‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】由于表示离校的距离，所以最终为零，在根据的变化快慢，判断出正确的图像.‎ ‎【详解】‎ 依题意可知，表示离校的距离，所以最终为零，故排除A,B两个选项.由于车的速度快，在图像上距离下降比较快；而步行较慢，距离下降比较慢.根据一项两点，可以判断出D选项符合题意.故选D.‎ ‎【点睛】‎ 本小题主要考查函数图像的识别，考查速度和距离变化快慢的关系，属于基础题.‎ ‎12．方程恰有三个不相等的实数根，则（ ）‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】对分成两类，画出与的图像，两个函数图像有三个不同的交点，由此求得的取值范围.‎ ‎【详解】‎ 当时，画出的图像，与的图像如下图所示：‎ 注意到和时，对应的函数值，将代入，解得、.由图像可知时，两个函数图像交点有个，符合题意.‎ 当时，画出的图像，与的图像如下图所示：‎ 注意到时，对应的函数值，将代入，解得、.由图像可知时，两个函数图像交点有个，符合题意.综上所述，本小题选D.‎ ‎【点睛】‎ 本小题主要考查三角函数的图像，考查对数函数的图像，考查方程的根于函数图像交点的对应，属于中档题.‎ 二、填空题 ‎13．已知全集U＝{0,1,2,3,4}，集合A＝{1,2,3}，B＝{2,4}，则(∁UA)∪B为____‎ ‎【答案】｛0，2，4｝‎ ‎【解析】根据集合补集与并集的定义求结果.‎ ‎【详解】‎ ‎.‎ ‎【点睛】‎ 本题考查集合补集与并集概念，考查基本求解能力，属基础题.‎ ‎14．已知tanα=2,则 =_____‎ ‎【答案】0‎ ‎【解析】将所求式子分子分母同时除以，变为只含有的表达式，代入的值求得最终的结果.‎ ‎【详解】‎ 将所求式子分子分母同时除以得.‎ ‎【点睛】‎ 本小题主要考查同角三角函数的基本关系式，考查齐次方程的应用，属于基础题.‎ ‎15．若扇形的面积是1㎝ 2它的周长是4㎝，则圆心角的弧度数是_________.‎ ‎【答案】2‎ ‎【解析】试题分析：设扇形的半径为r，弧长为l，则2r+l=4，,，∴，故圆心角的弧度数是 ‎【考点】本题考查了弧度的定义 点评：掌握扇形面积公式及弧度的定义是解决此类问题的关键 ‎16．已知函数在（－∞，+∞）上是增函数，则a的取值范围是___.‎ ‎【答案】（1,2］‎ ‎【解析】由于函数为 上的递增函数，故分段函数每一段都是递增函数，且在分界点第一段要在第二段上方，由此列不等式组，求得的取值范围.‎ ‎【详解】‎ 由于分段函数是上的增函数，故，解得.故填 ‎【点睛】‎ 本小题主要考查分段函数的单调性，考查指数函数以及一次函数的单调性，属于基础题.‎ 三、解答题 ‎17．设集合A＝{x|x＋1≤0或x－4≥0}，B＝{x|2a≤x≤a＋2}．若A∩B＝B，求实数a的取值范围．‎ ‎【答案】{a|a≤－3或a ≥2}．‎ ‎【解析】由于，故集合是集合的子集，分成和两类进行讨论，由此求得的取值范围.‎ ‎【详解】‎ ‎∵A∩B＝B，∴B⊆A. ‎ ‎①B＝∅时，满足B⊆A，则2a>a＋2⇒a>2， ‎ ‎②B≠∅时，则或 即a≤－3或a＝2. ‎ 综上所述，实数a的取值范围为{a|a≤－3或a ≥2}．‎ ‎【点睛】‎ 本小题主要考查集合交集的概念，考查子集的概念及应用，考查空集是任何集合的子集这一知识.属于基础题.‎ ‎18．已知，与的夹角为60°．‎ 试求：（1）；‎ ‎（2）与的夹角的余弦值．‎ ‎【答案】（1）（2）-‎ ‎【解析】（1）将两边平方，代入已知条件计算出结果，再开方求得的值.（2）利用（1）的方法，计算出的值，再利用夹角公式计算出与的夹角的余弦值.‎ ‎【详解】‎ ‎（1）|a＋b|2=a2＋b2＋2a·b ‎ ‎=9＋16＋2×3×4×cos60°=37‎ ‎∴|a＋b|= ‎ ‎（2）|a－b|2=a2＋b2－2a·b=9＋16－2×3×4×cos60°=13‎ ‎∴|a－b|= ‎ cosθ==‎ ‎【点睛】‎ 本小题主要考场向量数量积的运算，考查向量模的问题的求解策略，属于基础题.‎ ‎19．已知x∈[－，]，‎ ‎（1）求函数y＝cosx的值域；‎ ‎（2）求函数y＝－3sin2x－4cosx＋4的值域．‎ ‎【答案】（1）[－，1]（2）[－，]‎ ‎【解析】（1）根据余弦函数在上的单调性，求得函数的最大值以及最小值，由此求得值域.（2）将原函数用同角三角函数的基本关系式变为只含有的函数，利用配方法，结合二次函数的知识，求得函数的值域.‎ ‎【详解】‎ ‎(1)∵y＝cosx在[－，0]上为增函数，在[0，]上为减函数，‎ ‎∴当x＝0时，y取最大值1；‎ x＝时，y取最小值－. ‎ ‎∴y＝cosx的值域为[－，1]． ‎ ‎(2)原函数化为：y＝3cos2x－4cosx＋1，‎ 即y＝3(cosx－)2－，由(1)知，cosx∈[－，1]，‎ 故y的值域为[－，]．‎ ‎【点睛】‎ 本小题主要考查余弦函数在给定区间上的值域，考查含有三角函数的二次型函数求值域的方法，属于中档题.‎ ‎20．设函数,‎ ‎（1）求证: 不论为何实数总为增函数; ‎ ‎（2）确定的值,使为奇函数。‎ ‎【答案】（1）见证明；（2）见解析 ‎【解析】（1）先求得函数的定义域为，在定义域上任取，通过计算.证得不论为何值，函数为上的增函数.（2）利用列方程，求得的值.‎ ‎【详解】‎ ‎(1) 因为 的定义域为R,设 x1