- 858.00 KB
- 2021-04-12 发布
四川省泸县第二中学2019-2020学年高二下学期第一次在线月考
文科数学试题
注意事项:
1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
第I卷 选择题(60分)
一、选择题:本题共12小题,每小题5分,共60分。在每小题给的四个选项中,只有一项是符合题目要求的。
1.直线的倾斜角是
A. B. C. D.
2.命题“”的否定是
A. B.
C. D.
3.“”是“”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.已知命题“设、、,若,则”,则它的逆命题、否命题、逆否命题中真命题共有
A.0个 B.1个 C.2个 D.3个
5.过抛物线的焦点作直线交抛物线于两点,若线段的中点的横坐标为4,则
A.6 B.8 C.12 D.16
6. 若圆的半径为,则实数
A. B.-1 C.1 D.
7.已知圆,圆,则圆和圆的位置关系为
A.相切 B.内含 C.外离 D.相交
8.若方程表示焦点在轴上的椭圆,则锐角的取值范围是
A. B. C. D.
9.已知定点,点在圆上运动,则线段的中点的轨迹方程是
A. B.
C. D.
10.三棱锥的三条侧棱两两垂直,其长分别为,则该三棱锥的外接球的表面积
A. B. C. D.
11.若椭圆C:+=1的焦点为F1,F2,点P在椭圆C上,且|PF1|=4,则∠F1PF2=
A.30° B.60° C.120° D.150°
12.已知双曲线的左、右焦点分别为、,为左顶点,过点且斜率为的直线与双曲线的渐近线在第一象限的交点为,若,则该双曲线的离心率是
A. B. C. D.
第II卷 非选择题(90分)
二、填空题:本题共4小题,每小题5分,共20分。
13.不等式的解集用区间表示为______.
14.抛物线的焦点坐标是___________.
15.双曲线上一点到它的一个焦点的距离等于9,那么点到另一个焦点的距离等于_____.
16.已知点,若动点满足,则点的轨迹方程为__________.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)给定如下两个命题:命题“曲线是焦点在轴上的椭圆,其中为常数”;命题“曲线是焦点在轴上的双曲线,其中为常数”.已知命题“”为假命题,命题“”为真命题,求实数的取值范围.
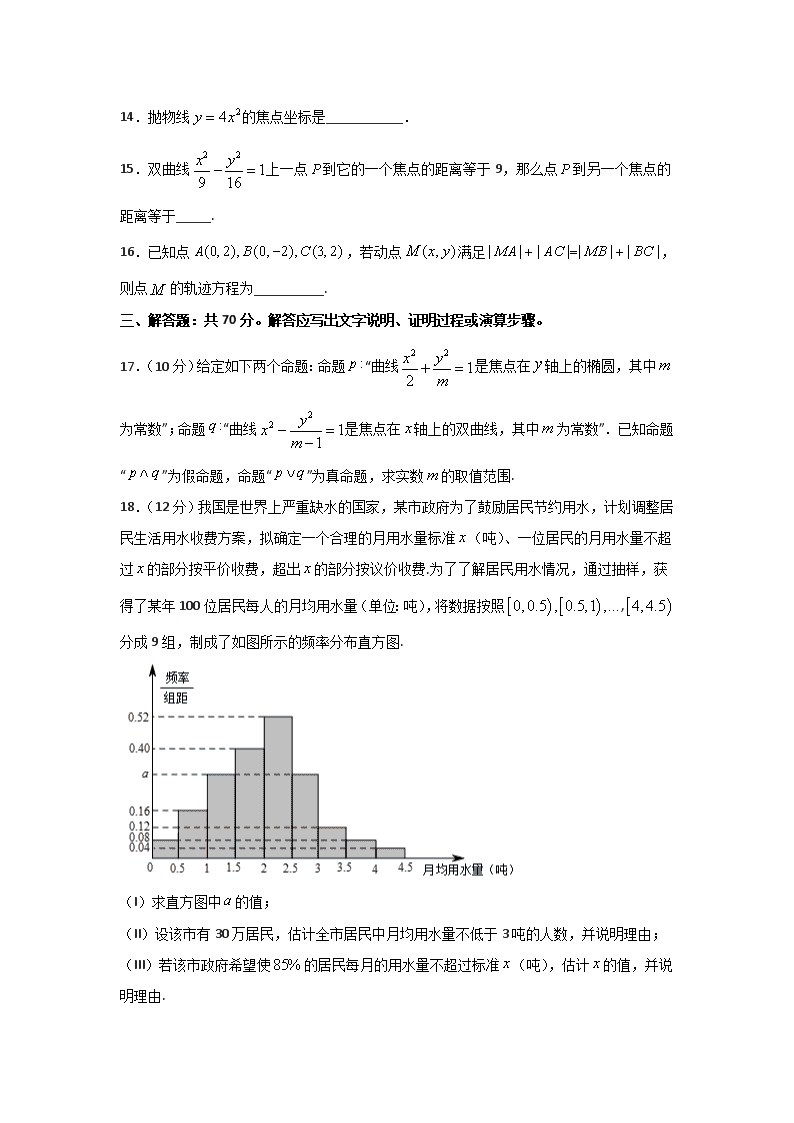
18.(12分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨)、一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(III)若该市政府希望使的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
19.(12分)已知动点到定点的距离比到定直线的距离小,其轨迹为.
(I)求的方程
(II)过点且不与坐标轴垂直的直线与交于、两点,线段的垂直平分线与轴交于点,求的取值范围.
20.(12分)足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x
2014
2015
2016
2017
2018
足球特色学校y(百个)
0.30
0.60
1.00
1.40
1.70
(I)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:,则认为y与x线性相关性很强;,则认为y与x线性相关性一般;,则认为y与x线性相关性较):
(II)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据:,
,.
21.(12分)如图,在平行四边形中,,,,分别是和的中点,将沿着向上翻折到的位置,连接,.
(I)求证:平面;
(II)若翻折后,四棱锥的体积,求的面积.
22.(12分)已知椭圆的一个焦点是F(1,0),O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点,若直线l绕点F任意转动,总有,求a的取值范围.
2020年春四川省泸县第二中学高二第一学月考试
文科数学试题参考答案
1.C 2.C 3.A 4.B 5.C 6.B 7.B 8.C 9.C 10.D 11.C 12.B
13. 14. 15.3或15 16.
17.若命题为真命题,则,若命题为真命题,则,
由题知与一真一假,若真假,则,此时无解.
若假真,则,得,
综上:实数的取值范围是.
18:(1)由频率分布直方图知,月均用水量在[0,0.5)中的频率为0.08×0.5=0.04,
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)中的频率分别为0.08,0.20,0.26,0.06,0.04,0.02.由0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1,解得a=0.30.
(2)由(1),100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计全市30万居民中月均用水量不低于3吨的人数为
300 000×0.12="36" 000.
(3)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85,
而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,
所以2.5≤x<3.
由0.3×(x–2.5)=0.85–0.73,解得x=2.9.
所以,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
19.解:(1)由题意知,动点到与定直线的距离与到定点的距离相等,由抛物线的定义可知,曲线的方程为:.
(2)由题意知直线存在斜率,设直线的方程为,,,中点,
则由得,
所以,,
则线段的中垂线的方程为,则,
又,即,
所以的取值范围是.
20.(1)由题得
所以,
y与x线性相关性很强.
(2)
,
,
关于的线性回归方程是.
当时,,即该地区2020年足球特色学校有244个.
(1)取的中点,连接,∵是的中点,∴
又∵是的中点,∴
∴,∴四边形是平行四边形,∴,
又∵平面,平面,
∴平面;
(2)取的中点,连接,过作的垂线于点,连接则
∵四棱锥的体积,而四边形的面积为,
设四棱锥的高为,则解得,∴,∴平面,
又∵平面,∴,又∵,∴平面,
又平面,∴,∴是的高,而在中,,
∴的面积.
22.(1)设为短轴的两个三等分点,为正三角形,
所以,,解得.,所以椭圆方程为.
(2)设
(ⅰ)当直线与轴重合时,
.
(ⅱ)当直线不与轴重合时,设直线的方程为:
整理得
因恒有,所以恒为钝角,
即恒成立.
又,所以对恒成立,
即对恒成立,
当时,最小值为0,所以,,
因为,即,解得或(舍去),
即,综合(i)(ii),的取值范围为.