- 274.00 KB
- 2021-04-12 发布
高二重点班期末考试
文科数学试题
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若复数z的共轭复数,则复数z的模长为( )
A.2
B.-1
C.5
D.
2.下列命题正确的是( )
A.命题“,使得x2-1<0”的否定是: ,均有x2-1<0.
B.命题“若x=3,则x2-2x-3=0”的否命题是:若x≠3,则x2-2x-3≠0.
C.“”是“”的必要而不充分条件.
D.命题“cosx=cosy,则x=y”的逆否命题是真命题.
3.下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程必经过点;
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A.0
B.1
C.2
D.3
4.抛物线的准线方程是( )
A.
B.
C.x=2
D.y=2
5.甲、乙两人练习射击, 命中目标的概率分别为和, 甲、乙两人各射击一次,目标被命中的概率为:
A. B. C. D.
6.下列函数中,满足“任意, ,且, ”的是
A. B. C. D.
7.曲线在处切线的斜率等于( )
A. 2e B. e C. 2 D. 1
8.不等式的解集是( )
A.(,+) B.(4,+) C.(﹣,﹣3)∪(4,+) D.(﹣,﹣3)∪(,+)
9.用反证法证明命题“若a2+b2=0(a,b∈R),则a,b全为0”,其反设正确的是( )
A.a,b至少有一个为0 B.a,b至少有一个不为0
C.a,b全部为0 D.a,b中只有一个为0
10.下列说法正确的是( )
A.如果两个复数的实部的差和虚部的差都等于0,那么这两个复数相等
B.ai是纯虚数(a∈R)
C.如果复数x+yi(x,y∈R)是实数,则x=0,y=0
D.复数a+bi(a,b∈R)不是实数
11.已知复平面内的平面向量,表示的复数分别是﹣2+i,3+2i,则向量所表示的复数的模为( )
A. B. C. D.
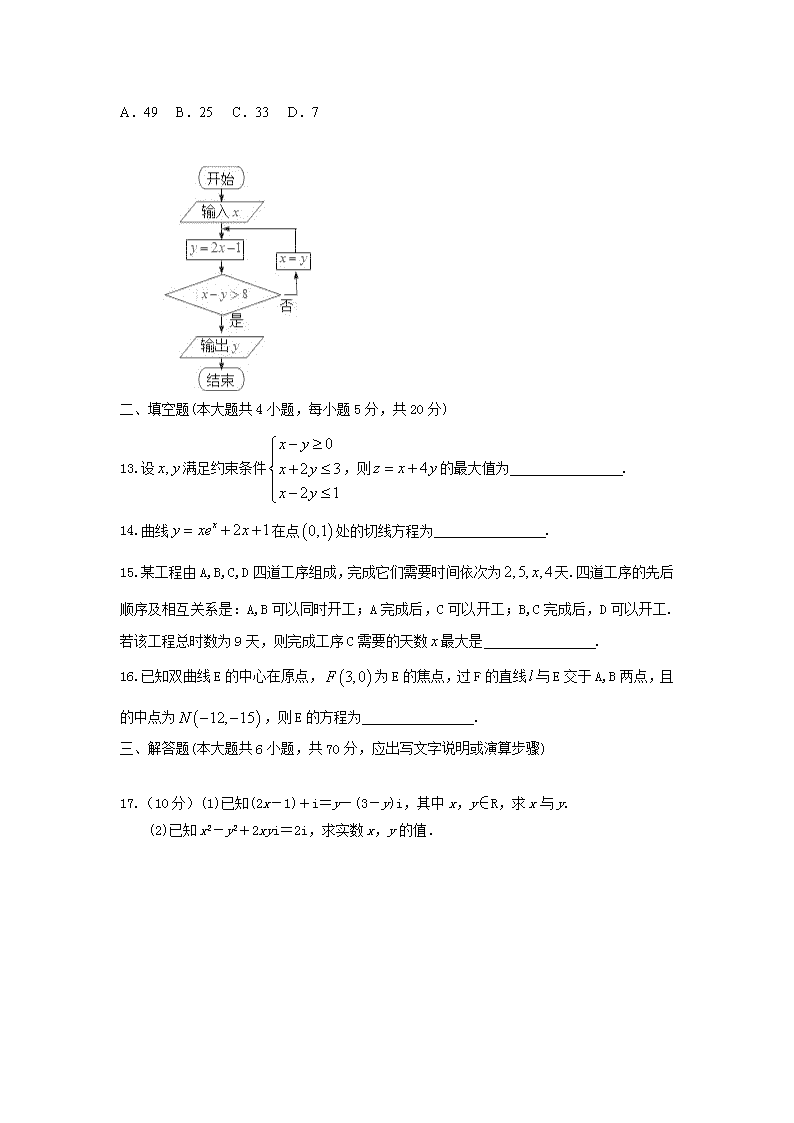
12.运行如图所示的程序框图.若输入x=5,则输出y的值为( )
A.49 B.25 C.33 D.7
二、填空题(本大题共4小题,每小题5分,共20分)
13.设满足约束条件,则的最大值为 .
14.曲线在点处的切线方程为 .
15.某工程由A,B,C,D四道工序组成,完成它们需要时间依次为天.四道工序的先后顺序及相互关系是:A,B可以同时开工;A完成后,C可以开工;B,C完成后,D可以开工.若该工程总时数为9天,则完成工序C需要的天数最大是 .
16.已知双曲线E的中心在原点,为E的焦点,过F的直线与E交于A,B两点,且的中点为,则E的方程为 .
三、解答题(本大题共6小题,共70分,应出写文字说明或演算步骤)
17.(10分)(1)已知(2x-1)+i=y-(3-y)i,其中x,y∈R,求x与y.
(2)已知x2-y2+2xyi=2i,求实数x,y的值.
18. (12分)已知函数在定义域上为增函数,且满足
(1)求的值. (2)解不等式
19.(12分)(Ⅰ)求下列各函数的导数:(1);
(2);
(Ⅱ)过原点O作函数f(x)=lnx的切线,求该切线方程.
20.(12分)设点O为坐标原点,椭圆的右顶点为A,上顶点为B,过点O且斜率为的直线与直线AB相交M,且.
(Ⅰ)求证:a=2b;
(Ⅱ)PQ是圆C:(x-2)2+(y-1)2=5的一条直径,若椭圆E经过P,Q两点,求椭圆E的方程.
21. (12分)在直角坐标系中,圆的方程为.
(Ⅰ)以坐标原点为极点,轴正半轴为极轴建立极坐标系,求的极坐标方程;
(Ⅱ)直线的参数方程是(为参数), 与交于两点,,求的斜率.
22.(12分)已知关于x的方程x2+(k+2i)x+2+ki=0有实根,求这个实根以及实数k的值.
文科数学答案
1-5.DBDDA 6-10AADBA 11-12CC
填空题
(13) 5 (14) (15) 3 (16)
三. 解答题
17.解析: (1)根据复数相等的充要条件得解得x=,y=4.
(2)∵x2-y2+2xyi=2i,
∴
解得或
18.(1)
(2) 解得
即原不等式的解集为(8,9)
19.解.(Ⅰ),∴;
(2);
(Ⅱ)设切点为T(x0,lnx0),∵,,解x0=e,
所以切点为T(e,1),故切线方程为.
20.解:(Ⅰ)∵A(a,0),B(0,b),,所以,
∴,解得a=2b,
(Ⅱ)由(Ⅰ)知a=2b,∴椭圆E的方程为即x2+4y2=4b2(1)
依题意,圆心C(2,1)是线段PQ的中点,且.
由对称性可知,PQ与x轴不垂直,设其直线方程为y=k(x-2)+1,
代入(1)得:
(1+4k2)x2-8k(2k-1)x+4(2k-1)2-4b2=0
设P(x1,y1),Q(x2,y2),则,,
由得,解得.
从而x1x2=8-2b2.
于是
解得b2=4,a2=16,∴椭圆E的方程为.
21.(I)由可得的极坐标方程
直线的直角坐标系方程得到:
所以的斜率为或.
22.解析: 设x=x0是方程的实根,代入方程并整理得(x+kx0+2)+(2x0+k)i=0.
由复数相等的条件得
解得或
∴方程的实根为x=或x=-,
相应的k的值为k=-2或k=2.