2014年山东省高考模拟数学（四）（文科） 14页

2014 年山东省高考模拟数学（四）（文科） 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 1.（5 分）已知集合 A={1，2，3，4}，B={x|x2=n，n∈A}，则 A∩B=（ ） A.{1，4} B.{﹣1，1} C.{1，2} D.∅ 解：根据 x2=n，n∈A，求出 x 的值，确定 B， ∵集合 A={1，2，3，4}，B={x|x2=n，n∈A}， ∴x=±1，± ，± ，±2， 即 B={﹣1，﹣1， ，﹣ ，﹣ ， ，﹣2，2}， 则 A∩B={1，2}. 答案：C 2.（5 分）复数 z=i（﹣2﹣i）（ i 为虚数单位）在复平面内所对应的点在（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 解析：化简可得复数 z=i（﹣2﹣i）=﹣2i﹣i2=1﹣2i， 故复数在复平面内所对应的点的坐标为（1，﹣2）在第四象限， 答案：D. 3.（5 分）已知命题：p：“∀x∈[1，2]，x2﹣a≥0”，命题 q：“∃x∈R，x2+2ax+2﹣a=0”， 若命题“￢p 且 q”是真命题，则实数 a 的取值范围是（ ） A.a≤﹣1 或 a=1 B.a≤﹣1 或 1≤a≤2 C.a≥1 D.a＞1 解析：因为命题“￢p 且 q”是真命题， 因此￢p 且 q，均为真命题， 命题 p：“∀x∈[1，2]，x2﹣a≥0”，为真命题，则 a≤1，所以￢p 为真命题时，a＞1； 命题 q：“∃x∈R，x2+2ax+2﹣a=0”，为真命题，则△=4a2﹣4（2﹣a）≥0，所以 a≤﹣2 或 a≥1， 所以 a＞1， 答案：D. 4.（5 分） “（2x﹣1）x=0”是“x=0”的（ ） A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 解析：若（2x﹣1）x=0 则 x=0 或 1x=x=0.2 ，不一定推出 x= 若 x=0，则（2x﹣1）x=0，即 x=0 推出（2x﹣1）x=0 所以“（2x﹣1）x=0”是“x=0”的 必要不充分条件. 答案：B 5.（5 分）若曲线 C1：x2+y2﹣2x=0 与曲线 C2：y（y﹣mx﹣m）=0 有四个不同的交点，则实数 m 的取值范围是（ ） A.（﹣ ， ） B.（﹣ ，0）∪（0， ） C.[﹣ ， ] D.（﹣∞，﹣ ）∪（ ，+∞） 解析：可知曲线 C1 表示一个圆，曲线 C2 表示两条直线 y=0 和 y﹣mx﹣m=0， 曲线 C1：x2+y2﹣2x=0 化为标准方程得：（x﹣1）2+y2=1，所以圆心坐标为（1，0），半径 r=1； 曲线 C2：y（y﹣mx﹣m）=0 表示两条直线 y=0 和 y﹣mx﹣m=0， 由直线 y﹣mx﹣m=0 可知：此直线过定点（﹣1，0）， 在平面直角坐标系中画出图象如图所示： 当直线 y﹣mx﹣m=0 与圆相切时，圆心到直线的距离 d= =r=1， 化简得：m2= ，解得 m=± ， 而 m=0 时，直线方程为 y=0，即为 x 轴，不合题意， 则直线 y﹣mx﹣m=0 与圆相交时，m∈（﹣ ，0）∪（0， ）. 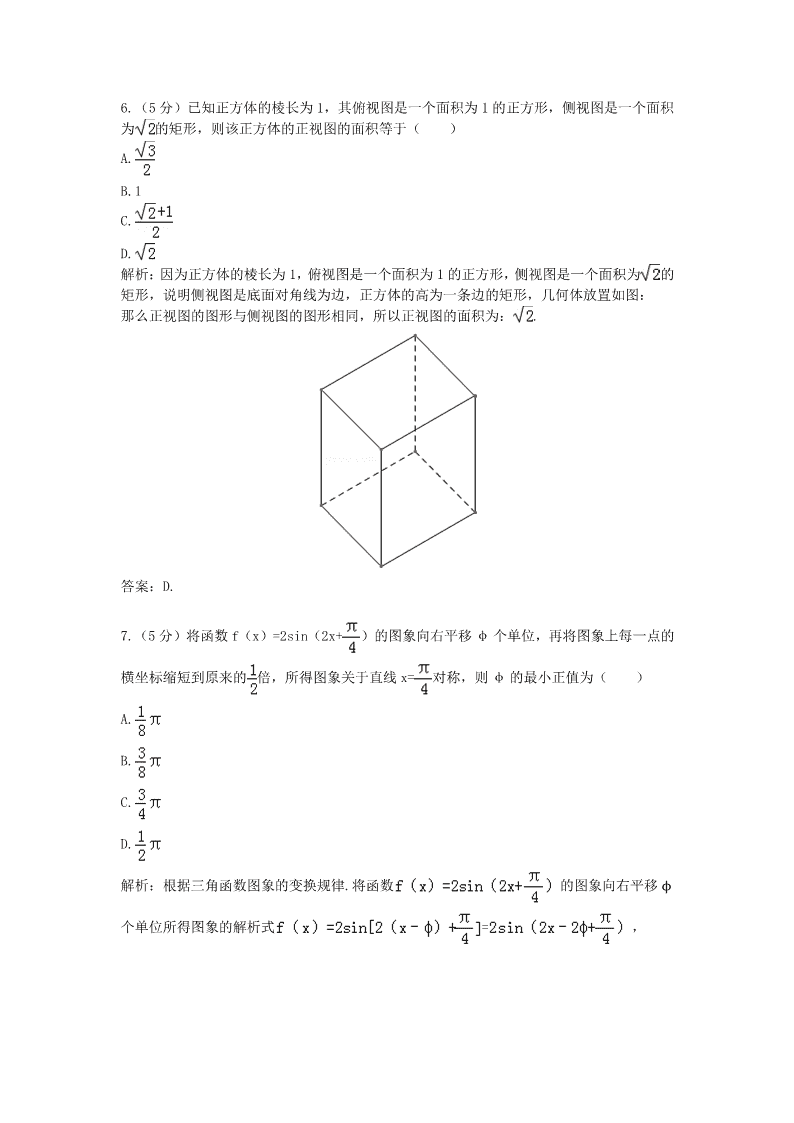答案：B 6.（5 分）已知正方体的棱长为 1，其俯视图是一个面积为 1 的正方形，侧视图是一个面积 为 的矩形，则该正方体的正视图的面积等于（ ） A. B.1 C. D. 解析：因为正方体的棱长为 1，俯视图是一个面积为 1 的正方形，侧视图是一个面积为 的 矩形，说明侧视图是底面对角线为边，正方体的高为一条边的矩形，几何体放置如图： 那么正视图的图形与侧视图的图形相同，所以正视图的面积为： . 答案：D. 7.（5 分）将函数 f（x）=2sin（2x+ ）的图象向右平移 φ 个单位，再将图象上每一点的 横坐标缩短到原来的 倍，所得图象关于直线 x= 对称，则 φ 的最小正值为（ ） A. B. C. D. 解析：根据三角函数图象的变换规律.将函数 的图象向右平移 ϕ 个单位所得图象的解析式 = ， 再将图象上每一点的横坐标缩短到原来的 倍所得图象的解析式 f（x） = 因为所得图象关于直线 对称，所以当 时函数取得最值，所以 =kπ+ ，k∈Z 整理得出 ϕ= ，k∈Z 当 k=0 时，ϕ取得最小正值为 . 答案：B. 8.（5 分）已知函数 f（x）是定义在 R 上的奇函数，且满足 f（x+2）=﹣f（x），当 0≤x≤1 时， ，则使 的 x 的值是（ ） A.2n（n∈Z） B.2n﹣1（n∈Z） C.4n+1（n∈Z） D.4n﹣1（n∈Z） 解析：因为 f（x）是奇函数且 f（x+2）=﹣f（x）， 那么 f（x+4）=﹣f（x+2）=f（x），即 函数 f（x）的周期 T=4. 因为当 0≤x≤1 时，f（x）= x，又 f（x）是奇函数，所以当﹣1≤x≤0 时，f（x）= x； 令 x=﹣ 解得：x=﹣1 而函数 f（x）是以 4 为周期的周期函数， 所以方程 f（x）=﹣ 的 x 的值是：x=4k﹣1，k∈Z. 答案：D. 9.（5 分）设函数 f（x）=ex+x﹣2，g（x）=lnx+x2﹣3.若实数 a，b 满足 f（a）=0，g（b） =0，则（ ） A.g（a）＜0＜f（b） B.f（b）＜0＜g（a） C.0＜g（a）＜f（b） D.f（b）＜g（a）＜0 解析：判断函数的单调性，利用二分法. 由于 y=ex 及 y=x﹣2 关于 x 是单调递增函数，因此函数 f（x）=ex+x﹣2 在 R 上单调递增， 分别作出 y=ex，y=2﹣x 的图象， ∵f（0）=1+0﹣2＜0，f（1）=e﹣1＞0，f（a）=0，∴0＜a＜1. 同理 g（x）=lnx+x2﹣3 在 R+上单调递增，g（1）=ln1+1﹣3=﹣2＜0，g（ ） = ，g（b）=0，∴ . ∴g（a）=lna+a2﹣3＜g（1）=ln1+1﹣3=﹣2＜0， f（b）=eb+b﹣2＞f（1）=e+1﹣2=e﹣1＞0. ∴g（a）＜0＜f（b）. 答案：A. 10.（5 分）已知函数 ，且函数 y=f（x）﹣x 恰有 3 个不 同的零点，则实数 a 的取值范围是（ ） A.（0，+∞） B.[﹣1，0） C.[﹣1，+∞） D.[﹣2，+∞） 解析：当 x≥0 时，f（x）=f（x﹣1）， 所以此时周期是 1，当 x∈[﹣1，0）时，y=﹣x2﹣2x+a= ﹣（x+1）2+1+a， 图象为开口向下的抛物线，对称轴 x=﹣1，顶点（﹣1，1+a）， （1）如果 a＜﹣1，函数 y=f（x）﹣x 至多有 2 个不同的零点； （2）如果 a=﹣1，则 y 有一个零点在区间（﹣1，0），有一个零点在（﹣∞，﹣1），一个零 点是原点； （3）如果 a＞﹣1，则有一个零点在（﹣∞，﹣1）， y 右边有两个零点， 综上可得：实数 a 的取值范围是[﹣1，+∞） 答案：C. 二、填空题：本大题共 5 小题，每小题 5 分，共 25 分. 11.（5 分）观察等式： ， ，根据以上规律，写出第 四个等式为： . 解析：类比推理 观察前面两个等式可得： 出第四个等式为： + + + + = ， 答案： + + + + = . 12.（5 分）在△ABC 中， ， ，则 AB 边的长度为 . 解析：将向量 用 ， 表示，即 = = +| |=﹣ 1+| |=2，因此| |=3. 答案：3. 13.（5 分）各项均为正数的等比数列{an}满足 a1a7=4，a6=8，若函数 f（x）=a1x+a2x2+a3x3+…+a10x10 的导数为 f′（x），则 f′（ ）= . 解析：等比数列{an}，由已知，所以 ，解得 ，所以 . 所以 f′（x）= …+ ， 因为 =n×2n﹣3×21﹣n= ， 所以 = = = . 答案： . 14.（5 分）设 m≥2，点 P（x，y）为 所表示的平面区域内任意一点，M（0，﹣5）， O 坐标原点，f（m）为 的最小值，则 f（m）的最大值为 . 解：易知 =﹣5y，设 z= =﹣5y， 作出不等式组对应的平面区域如图： 即当 y 取得最大值时，z 取得最小值，则由 ，解得 ， ∴f（m）=﹣5× ， ∵m≥2，∴当 m=2 时，f（m）取得最大值 f（2）=﹣ ， 答案： 15.（5 分）给出下列四个命题： ①命题“∀x∈R，cosx＞0”的否定是“∃x∈R，cosx≤0”； ②若 0＜a＜1，则函数 f（x）=x2+ax﹣3 只有一个零点； ③函数 y=sin（2x﹣ ）的一个单调增区间是[﹣ ， ]； ④对于任意实数 x，有 f（﹣x）=f（x），且当 x＞0 时，f′（x）＞ 0，则当 x＜0 时，f′（x） ＜0. ⑤若 m∈（0，1]，则函数 y=m+ 的最小值为 2 ； 其中真命题的序号是 （把所有真命题的序号都填上）. 解析：①命题“∀x∈R，cosx＞0”的否定是“∃x∈R，cosx≤0”，正确； ②当 0＜a＜1 时，y=ax 为减函数，y=3﹣x2 为开口向下的二次函数，两曲线有两个交点，函 数 f（x）=x2+ax﹣3 有两个零点，故②错误； ③由﹣ ≤2x﹣ ≤ 得：﹣ ≤x≤ ，即函数 y=sin（2x﹣ ）的一个单调增区间 是[﹣ ， ]，即③正确； ④∵f（﹣x）=f（x），故 y=f（x）为偶函数，又当 x＞0 时，f′（x）＞0，∴y=f（x）在 区间（0，+∞）上单调递增， 由偶函数在对称区间上单调性相反知，y=f（x）在区间（﹣∞，0）上单调递减，即当 x＜0 时，f′（x）＜0，故④正确； ⑤∵y=m+ ，∴y′=1﹣ ，∴当 m∈（0，1]时，y′＜0，即函数 y=m+ 在区间（0，1]上 单调递减， ∴当 x=1 时，ymin=1+3=4，故⑤错误； 综上所述，真命题的序号是①③④. 答案：①③④. 三、解答题本大题共 6 小题，共 75 分. 16.（12 分）已知函数 . （1）求 的值； （2）若 ，求 . 解析：（1）将 x= 直接代入函数解析式求值. （2）利用同角三角函数的基本关系求出 sinθ 的值，利用两角和与差公式求值. 答案：（1） （2）∵ ， ， ∴ . 17.（12 分）某校研究性学习小组，为了分析 2012 年某小国的宏观经济形势，查阅了有关 材料，得到 2011 年和 2012 年 1﹣5 月该国 CPI 同比（即当年某月与前一年同月比）的增长 数据（见下表），但 2012 年 3，4，5 三个月的数据（分别记为 x，y，z）没有查到，有的同 学清楚记得 2012 年 1﹣5 月的 CPI 数据成等差数列. （Ⅰ）求 x，y，z 的值； （Ⅱ）求 2012 年 1﹣5 月该国 CPI 数据的方差； （Ⅲ）一般认为，某月 CPI 达到或超过 3 个百分点就已经通货膨胀，而达到或超过 5 个百分 点则严重通货膨胀.现随机的从下表 2011 年的五个月和 2012 年的五个月的数据中各抽取一 个数据，求相同月份 2011 年通货膨胀，并且 2012 年严重通货膨胀的概率.附表：2011 年和 2012 年 1﹣5 月 CPI 数据（单位：百分点 注：1 个百分点=1%） 年份 月份 1 2 3 4 5 2011 2.7 2.4 2.8 3.1 2.9 2012 4.9 5.0 x y z 解析：（Ⅰ）因为呈现的等差数列，由图得该数列的公差为 0.1，可求 x、y、z 的值； （Ⅱ）求出 2012 年 1-5 月的平均数，再利用方差公式求方差. （Ⅲ）用（m，n）表示随机地从 2011 年的五个月和 2012 年的五个月的数据中各抽取一个数 据的基本事件，列举抽取数据的情况，分析可得事件“相同月份 2011 年通货膨胀，并且 2012 年严重通货膨胀”包含的基本事件的数目，由古典概型公式，计算可得答案. 答案：（Ⅰ）依题意得 4.9，5.0，x，y，z 成等差数列，所以公差 d=5.0﹣4.9=0.1， 故 x=5.0+0.1=5.1，y=x+0.1=5.2，z=y+0.1=5.3； （Ⅱ）由（Ⅰ）知 2012 年 1～5 月该国 CPI 的数据为：4.9，5.0，5.1，5.2，5.3， ∴ ， ∴ =0.02； （Ⅲ）根据题意，用 m 表示 2011 年的数据，n 表示 2012 年的数据，则（m，n）表示随机地 从 2011 年的五个月和 2012 年的五个月的数据中各抽取一个数据的基本事件， 则所有基本事件有：（2.7，4.9），（2.7，5.0），（2.7，5.1），（ 2.7，5.2），（ 2.7，5.3）， （2.4，4.9），（ 2.4，5.0），（2.4，5.1），（2.4，5.2），（ 2.4，5.3）， （2.8，4.9），（ 2.8，5.0），（2.8，5.1），（2.8，5.2），（ 2.8，5.3）， （3.1，4.9），（ 3.1，5.0），（3.1，5.1），（3.1，5.2），（ 3.1，5.3）， （2.9，4.9），（ 2.9，5.0），（2.9，5.1），（2.9，5.2），（ 2.9，5.3）；共 25 个基本事件； 其中满足相同月份 2011 年通货膨胀，并且 2012 年严重通货膨胀的基本事件有（3.1，5.0）， （3.1，5.1），（ 3.1，5.2），（3.1，5.3），有 4 个基本事件； ∴P= =0.16，即相同月份 2011 年通货膨胀，并且 2012 年严重通货膨胀的概率为 0.16. 18.（12 分）如图 1，在边长为 1 的等边三角形 ABC 中，D，E 分别是 AB，AC 边上的点，AD=AE， F 是 BC 的中点，AF 与 DE 交于点 G，将△ABF 沿 AF 折起，得到如图 2 所示的三棱锥 A﹣BCF， 其中 BC= . （1）证明：DE∥平面 BCF； （2）证明：CF⊥平面 ABF； （3）当 AD= 时，求三棱锥 F﹣DEG 的体积 VF﹣DEG. 分析： （1）利用线面平行的判定定理，易知 DE∥BC，可证 DE∥平面 BCF. （2）可证得 AF⊥CF ，利用勾股定理和已知数据 CF⊥BF，利用线面垂直的判定定理可证 CF ⊥平面 ABF. （3）利用等积法 ，运算求得结果. 答案：（1）在等边三角形 ABC 中，AD=AE，∴ ，在折叠后的三棱锥 A﹣BCF 中也成立， ∴DE∥BC. 又∵DE⊄平面 BCF，BC⊂平面 BCF， ∴DE∥平面 BCF. （2）在等边三角形 ABC 中，F 是 BC 的中点，所以 AF⊥BC，即 AF⊥CF ①，且 . ∵在三棱锥 A﹣BCF 中， ，∴BC2=BF2+CF2，∴CF⊥BF②. 又∵BF∩AF=F，∴CF⊥平面 ABF. （3）由（1）可知 GE∥CF，结合（2）可得 GE⊥平面 DFG. ∴ = . 19.（12 分）已知等比数列{an}的前 n 项和 ﹣a，数列{bn}（bn＞0）的首项为 b1=a，且其前 n 项和 Sn 满足 Sn+Sn﹣1=1+2 （n≥2，n∈N*） （Ⅰ）求数列{an}和{bn}的通项公式； （Ⅱ）若数列 的前 n 项和为 Pn. 解析： （1）数列{an}成等比数列， 可得 = ，解得 a=1，设 数列{an}的公比为 q，则 .由 bn＞0，得 ，数列 构成一个 首项为 1，公差为 1 的等差数列，由此能求出数列{an}和{bn}的通项公式. （2） = ，利用裂项相消求和法能求 出数列 的前 n 项和为 Pn. 答案：（1）根据已知条件知： = ， 有数列{an}成等比数列，得 ， 即 = ，解得 a=1， 设数列{an}的公比为 q，则 ， 所以 …（3 分） ，其中 n≥2，n∈N*， 又 bn＞0，得 ， 数列 构成一个首项为 1，公差为 1 的等差数列， 所以 ， 所以 ，当 n≥2，n∈N*时 ， b1=1 也适合这个公式， 所以 bn=2n﹣1（n∈N*） （6 分） （2）由（1）知 = ， 则 Pn= = .…（12 分） 20.（13 分）已知函数 f（x）=mx﹣ ，g（x）=2lnx （1）当 m=2 时，求曲线 y=f（x）在点（1，f（1））处的切线方程； （2）当 m=1 时，证明方程 f（x）=g（x）有且仅有一个实数根； （3）若 x∈（1，e]时，不等式 f（x）﹣g（x）＜2 恒成立，求实数 m 的取值范围. 解析：（1）当 m=2 时，确定 f（x），求导确定斜率，利用点斜式求出切线方程. （2）当 m=1 时，构造 h（x）=f（x）-g（x）,求出 h'（x），判断在定义域上的单调性，判 定 的符号，根据根的存在性定理可得结论； （3）即 恒成立，即 m（x2﹣1）＜2x+2xlnx 恒成立，利用分离变量法， 研究右侧的最值，讨论 m 的取值范围. 答案：（ 1）m=2 时， ， ， 切点坐标为（1，0）， ∴切线方程为 y=4x﹣4…（2 分） （2）m=1 时，令 ， ， ∴h（x）在（0，+∞）上为增函数.…（4 分） 又 ， ∴y=h（x）在（0，+∞）内有且仅有一个零点 ∴在（0，+∞）内 f（x）=g（x）有且仅有一个实数根 …（6 分） （或说明 h（1）=0 也可以） （3） 恒成立，即 m（x2﹣1）＜2x+2xlnx 恒成立， 又 x2﹣1＞0，则当 x∈（1，e]时， 恒成立， 令 ，只需 m 小于 G（x）的最小值， ， ∵1＜x≤e，∴lnx＞0，∴当 x∈（1，e]时 G'（x）＜0， ∴G（x）在（1，e]上单调递减， ∴G（x）在（1，e]的最小值为 ， 则 m 的取值范围是 . …（12 分） 21.（14 分）椭圆 C： =1（a＞b＞0）的离心率 ，a+b=3. （1）求椭圆 C 的方程； （2）如图，A，B，D 是椭圆 C 的顶点，P 是椭圆 C 上除顶点外的任意点，直线 DP 交 x 轴于 点 N 直线 AD 交 BP 于点 M，设 BP 的斜率为 k，MN 的斜率为 m，证明 2m﹣k 为定值. 解析： （1）根据离心率及 a+b=3，结合条件 a2=b2+c2 列式求出 a，b，确定椭圆方程. （2）需要求出 P，M，N 的坐标，利用两点求斜率 m，代入整理出 2m-k 是定值. 答案：（1）因为 ，所以 ，即 a2=4b2，a=2b. 又 a+b=3，得 a=2，b=1. 所以椭圆 C 的方程为 ； （2）因为 B（2，0）， P 不为椭圆顶点，则可设直线 BP 的方程为 . 联立 ，得（4k2+1）x2﹣16k2x+16k2﹣4=0. 所以 ， . 则 . 所以 P（ ）. 又直线 AD 的方程为 . 联立 ，解得 M（ ）. 由三点 D（0，1）， P（ ）， N（x，0）共线， 得 ，所以 N（ ）. 所以 MN 的斜率为 = . 则 . 所以 2m﹣k 为定值 .