- 280.44 KB
- 2021-04-12 发布
2018届高三年级第四次月考数学(理科)试卷
命题:赵立明
一、选择题(本题共12道小题,每小题5分,共60分)
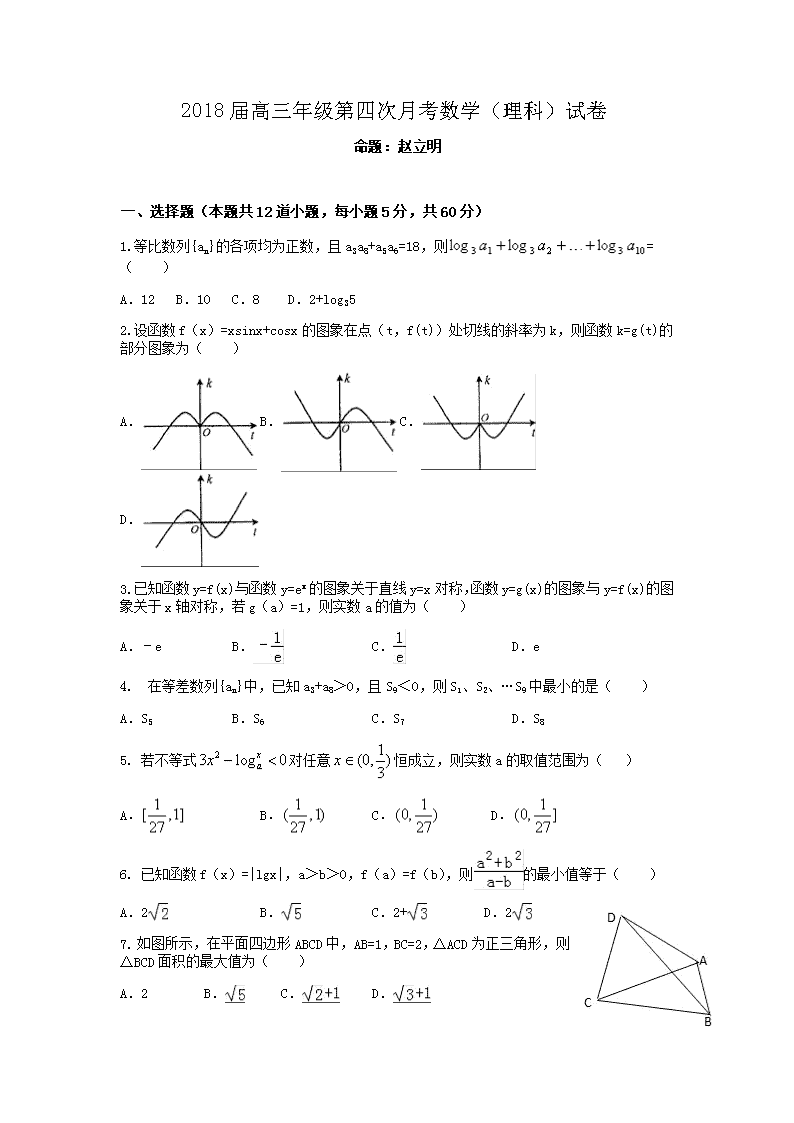
1.等比数列{an}的各项均为正数,且a3a8+a5a6=18,则=( )
A.12 B.10 C.8 D.2+log35
2.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的部分图象为( )
A. B. C.D.
3.已知函数y=f(x)与函数y=ex的图象关于直线y=x对称,函数y=g(x)的图象与y=f(x)的图象关于x轴对称,若g(a)=1,则实数a的值为( )
A.﹣e B. C. D.e
4. 在等差数列{an}中,已知a3+a8>0,且S9<0,则S1、S2、…S9中最小的是( )
A.S5 B.S6 C.S7 D.S8
5. 若不等式对任意恒成立,则实数a的取值范围为( )
A. B. C. D.
6. 已知函数f(x)=|lgx|,a>b>0,f(a)=f(b),则的最小值等于( )
A.2 B. C.2+ D.2
7. 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
A.2 B. C. D.
8. 如图是函数图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有,则( )
A.f(x)在上是增函数
B.f(x)在上是减函数
C.f(x)在上是增函数
D.f(x)在上是减函数
9. 如图,在△OMN中,A,B分别是OM,ON的中点,若=x+y(x,y∈R),且点P落在四边形ABNM内(含边界),则的取值范围是( )
A.[,] B.[,]
C.[,] D.[,]
10. 在平行四边形ABCD中,∠A=,边AB,AD的长分别为2,1,若M,N分别是边BC,CD上的点,且满足=,则•的取值范围是( )
A.[1,4] B.[2,5] C.[2,4] D.[1,5]
11. 已知函数g(x)满足g(x)=g′(1)ex﹣1﹣g(0)x+,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
A.(﹣∞,2] B.(﹣∞,3] C.[1,+∞) D.[0,+∞)
12. 设f(x)是定义在R上的函数,其导函数为f(x),若f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)>ex+2016(其中e为自然对数的底数)的解集为( )
A.(﹣∞,0)∪(0,+∞) B.(0,+∞)
C.(﹣∞,0) D.(﹣∞,0)∪(1,+∞)
二、填空题(本题共4道小题,每小题5分,共20分)
13.若集合A={﹣4,2a﹣1,a2},B={a﹣5,1﹣a,9},且A∩B={9},则a的值是 .
14. 已知Sn是等差数列{an}的前n项和,若a1=﹣2017, =6,则S2017= .
15.已知f(x)=,则函数y=2f2(x)﹣3f(x)的零点个数为 .
16. 已知函数,若正实数a,b满足f(4a)+f(b﹣9)=0,则的最小值为 .
三、解答题
17. (10分)已知定义域为R的函数f(x)=是奇函数.
(1)求a,b的值;
(2)用定义证明f(x)在(﹣∞,+∞)上为减函数;
(3)若对于任意t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的范围.
18. (12分)
在△ABC中,内角A,B,C的对边分别为a,b,c,已知,且,
(Ⅰ)求△ABC的面积.
(Ⅱ)已知等差数列{an}的公差不为零,若a1cosA=1,且a2,a4,a8成等比数列,求{}的前n项和Sn.
19. (12分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且cos2A+cos2B+2sinAsinB=2coc2C.
(Ⅰ)求角C的值;
(Ⅱ)若△ABC为锐角三角形,且,求a﹣b的取值范围.
20. (12分)
已知=(5cosx,cosx),=(sin x,2cos x),设函数f(x)=++.
(1)求函数f(x)的最小正周期和对称中心;
(2)当x∈[,]时,求函数f(x)的值域.
21. (12分)
已知:A、B、C是△ABC的内角,a,b,c分别是其对边长,向量=(,cosA+1),=(sinA,﹣1),⊥
(Ⅰ)求角A的大小;
(Ⅱ)若,a=2,cosB=,求b的长.
22. (12分)
已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[,1]上的最小值;
(2)若∀x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若∀x>0,不等式f()﹣1≥+恒成立,求a的取值范围.
2018届高三年级第四次月考数学试卷(理科)答题卡
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(本大题共4个小题,每小题5分,共20分)
13、 14、 15、 16、
三、解答题(共70分)
17、(10分)
18、(12分)
19、(12分)
20、(12分)
21、(12分)
22、(12分)
2018届高三年级第四次月考数学试卷(理科)答案
1.B 2.B 3.C 4.A 5.A 6.A 7.D 8.A 9.C 10.B 11.C 12.B
13.﹣3 14.﹣2017 15.5 16.1
17.
【解答】解:(1)∵f(x)为R上的奇函数,∴f(0)=0,可得b=1
又∵f(﹣1)=﹣f(1)
∴=﹣,解之得a=1
经检验当a=1且b=1时,f(x)=,满足f(﹣x)=﹣f(x)是奇函数. …
(2)由(1)得f(x)==﹣1+,
任取实数x1、x2,且x1<x2
则f(x1)﹣f(x2)=﹣=
∵x1<x2,可得,且
∴f(x1)﹣f(x2)>0,即f(x1)>f(x2),函数f(x)在(﹣∞,+∞)上为减函数; …
(3)根据(1)(2)知,函数f(x)是奇函数且在(﹣∞,+∞)上为减函数.
∴不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,即f(t2﹣2t)<﹣f(2t2﹣k)=f(﹣2t2+k)
也就是:t2﹣2t>﹣2t2+k对任意的t∈R都成立.
变量分离,得k<3t2﹣2t对任意的t∈R都成立,
∵3t2﹣2t=3(t﹣)2﹣,当t=时有最小值为﹣
∴k<﹣,即k的范围是(﹣∞,﹣). …
18.
解:(Ⅰ)∵在△ABC中,内角A,B,C的对边分别为a,b,c,
,且,
∴由正弦定理得:,即:b2+c2﹣a2=bc,
∴由余弦定理得:,
又∵0<A<π,∴,…(3分)
∵且,即:5acosC=﹣5,即:,
与联立解得:c=12,…
∴△ABC的面积是:;…(6分)
(Ⅱ)数列{an}的公差为d且d≠0,由a1cosA=1,得a1=2,
又a2,a4,a8成等比数列,得,解得d=2…(8分)
∴an=2+(n﹣1)×2=2n,有an+2=2(n+2),
则…(10分)
∴
=.…(12分)
19.解:(Ⅰ)∵cos2A+cos2B+2sinAsinB=2coc2C,
∴1﹣2sin2A+1﹣2sin2B+2sinAsinB=2(1﹣sin2C),
即sin2C=sin2A+sin2B﹣sinAsinB,…
由正弦定理得:c2=a2+b2﹣ab,
∴,
且角C角为三角形的内角,即.…
(Ⅱ)由(Ⅰ)知…(7分)
由得,a=2sinA,b=2sinB,
,…(10分)
∵△ABC为锐角三角形,,又∵,
∴A∈(,),
∴A﹣∈(﹣,),
∴,即a﹣b的取值范围为(﹣1,1).…(12分)
20.
【解答】解:(1)f(x)=
=5sin xcos x+2cos2x+4cos2x+sin2x+
=5sin xcos x+5cos2x+
=sin 2x+5•+=5sin(2x+)+5;
∴f(x)的最小正周期为T=π,对称中心为;
(2)f(x)=5sin(2x+)+5;
由≤x≤,得≤2x+≤;∴﹣≤sin(2x+)≤1;
∴当≤x≤时,函数f(x)的值域为[,10].
21.【解答】解:(Ⅰ)∵=(,cosA+1),=(sinA,﹣1),⊥,
∴sinA﹣cosA﹣1=0,即sinA+cosA=1,
整理得:2(sinA+cosA)=1,即sin(A+)=,
∴A+=,则A=;
(Ⅱ)由cosB=,得到sinB=,∵a=2,sinA=,
∴由正弦定理=得:b===.
22.【解答】解:(1)a=0时,f(x)=xe2x﹣lnx,
∴,,
∴函数f′(x)在(0,+∞)上是增函数,
又函数f′(x)的值域为R,
故∃x0>0,使得f′(x0)=(2x0+1)e﹣=0,
又∵,∴,∴当x∈[]时,f′(x)>0,
即函数f(x)在区间[,1]上递增,∴.
(2),
由(1)知函数f′(x)在(0,+∞)上是增函数,且∃x0>0,使得f′(x0)=0,
进而函数f(x)在区间(0,x0)上递减,在(x0,+∞)上递增,
﹣lnx0﹣ax0,
由f′(x0)=0,得:(2x0+1)e﹣﹣a=0,
∴,∴f(x0)=1﹣lnx0﹣2x02,
∵∀x>0,不等式f(x)≥1恒成立,
∴1﹣lnx0﹣2x02e≥1,∴lnx0+2x02≤0,
设h(x0)=lnx0+2xe,则h(x0)为增函数,且有唯一零点,设为t,
则h(t)=lnt+2t2e2t=0,则﹣lnt=2t2e2t,即,
令g(x)=xex,则g(x)单调递增,且g(2t)=g(),
则2t=ln,即,∵a=(2x0+1)﹣在(0,t]为增函数,
则当x0=t时,a有最大值, =,
∴a≤2,∴a的取值范围是(﹣∞,2].
(3)由f()﹣1≥,得,
∴xlnx﹣x﹣a≥,∴a对任意x>0成立,
令函数g(x)=xlnx﹣x﹣,∴,
当x>1时,g′(x)>0,当0<x<1时,g′(x)<0,
∴当x=1时,函数g(x)取得最小值g(1)=﹣1﹣=﹣1﹣,
∴a≤﹣1﹣. ∴a的取值范围是(﹣∞,﹣1﹣).
【来.源:全,品…中&高*考*网】