- 448.00 KB
- 2021-04-12 发布
全*品*高*考*网, 用后离不了!2016-2017学年广东省汕头市潮南实验中学高二(上)10月月考数学试卷(文科)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一项是符合要求的.)
1.设M={x|x=a2+1,a∈R},P={y|y=b2﹣4b+5,b∈R},则下列关系正确的是( )
A.M=P B.M⊊P
C.P⊊M D.M与P没有公共元素
2.已知点P(sinπ,cosπ)落在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A. B. C. D.
3.一个几何体的三视图如图,则该几何体的体积为( )
A.π B. C. D.
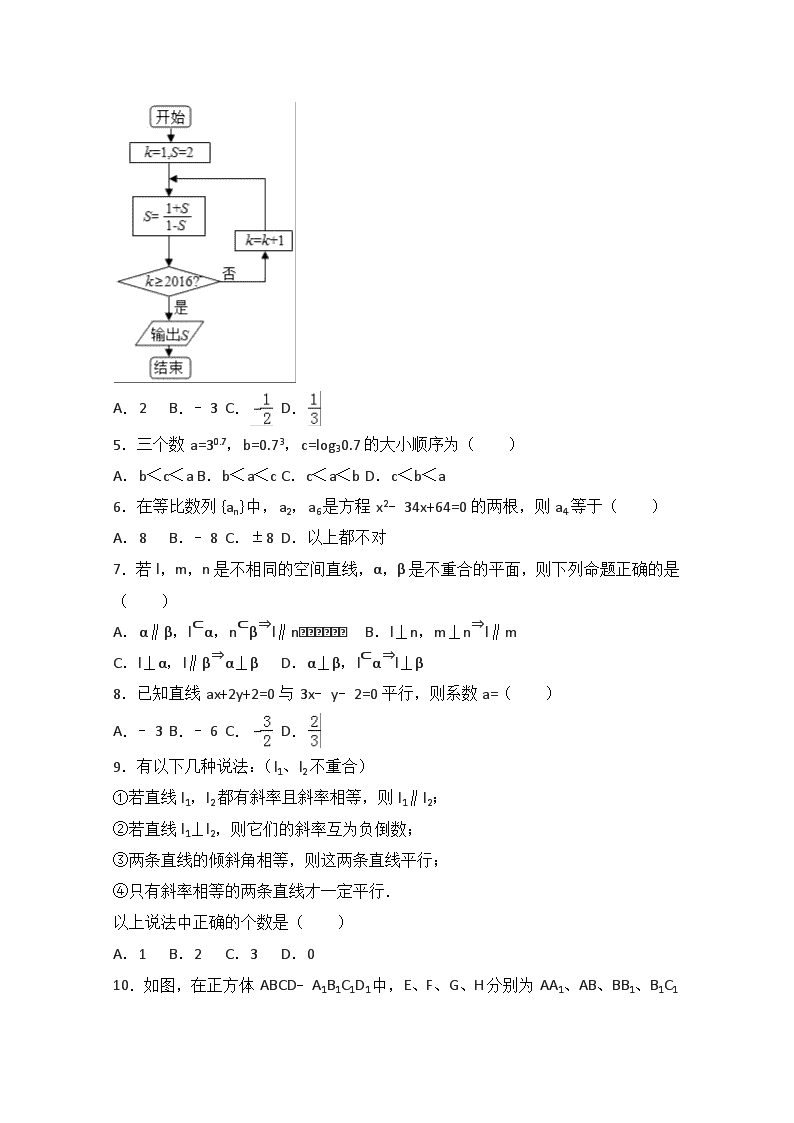
4.执行如图的程序框图,则输出S的值为( )
A.2 B.﹣3 C. D.
5.三个数a=30.7,b=0.73,c=log30.7的大小顺序为( )
A.b<c<a B.b<a<c C.c<a<b D.c<b<a
6.在等比数列{an}中,a2,a6是方程x2﹣34x+64=0的两根,则a4等于( )
A.8 B.﹣8 C.±8 D.以上都不对
7.若l,m,n是不相同的空间直线,α,β是不重合的平面,则下列命题正确的是( )
A.α∥β,l⊂α,n⊂β⇒l∥n B B.l⊥n,m⊥n⇒l∥m
C.l⊥α,l∥β⇒α⊥β D.α⊥β,l⊂α⇒l⊥β
8.已知直线ax+2y+2=0与3x﹣y﹣2=0平行,则系数a=( )
A.﹣3 B.﹣6 C. D.
9.有以下几种说法:(l1、l2不重合)
①若直线l1,l2都有斜率且斜率相等,则l1∥l2;
②若直线l1⊥l2,则它们的斜率互为负倒数;
③两条直线的倾斜角相等,则这两条直线平行;
④只有斜率相等的两条直线才一定平行.
以上说法中正确的个数是( )
A.1 B.2 C.3 D.0
10.如图,在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1
的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
11.若直线y=kx+1与圆x2+y2+kx﹣y﹣9=0的两个交点恰好关于y轴对称,则k等于( )
A.0 B.1 C.2 D.3
12.从直线x﹣y+3=0上的点向圆x2+y2﹣4x﹣4y+7=0引切线,则切线长的最小值为( )
A. B. C. D.﹣1
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上.)
13.若直线m被两平行直线l1:x﹣y+1=0,l2:x﹣y+3=0所截得的线段长为2,则m的倾斜角可以是 .
①15° ②30° ③45° ④60° ⑤75°.
14.已知矩形ABCD中AB=3,BC=a,若PA⊥平面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有两个时,a的取值范围是 .
15.如图,半圆的直径AB=2,O为圆心,C为半圆上不同于A,B的任意一点,若P为半径OC上的动点,则的最小值是 .
16.若x∈R,有意义且满足x2+y2﹣4x+1=0,则的最大值为 .
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)
17.圆x2+y2=8内有一点P0(﹣1,2),AB为过点P0且倾斜角为α的弦;
(1)当时,求AB的长;
(2)当弦AB被点P0平分时,求直线AB的方程.
18.在△ABC中,a=3,b=2,∠B=2∠A.
(Ⅰ)求cosA的值;
(Ⅱ)求c的值.
19.如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
(1)求证:AC⊥BF;
(2)求证:BF⊥平面ACFD.
20.已知数列{log2(an﹣1)}(n∈N*)为等差数列,且a1=3,a3=9.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明++…+<1.
21.如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N﹣BCM的体积.
22.已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.
(1)求证:对任意的m,直线l与圆C总有两个不同的交点;
(2)设l与圆C交于A,B两点,若|AB|=,求l的倾斜角;
(3)求弦AB的中点M的轨迹方程.
2016-2017学年广东省汕头市潮南实验中学高二(上)10月月考数学试卷(文科)
参考答案与试题解析
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一项是符合要求的.)
1.设M={x|x=a2+1,a∈R},P={y|y=b2﹣4b+5,b∈R},则下列关系正确的是( )
A.M=P B.M⊊P
C.P⊊M D.M与P没有公共元素
【考点】集合的相等.
【分析】根据题意,将集合M、P变形可得:M={x|x≥1},P={x|x≥1},分析可得答案.
【解答】解:根据题意,M={x|x=a2+1,a∈R}={x|x≥1},
P={y|y=b2﹣4b+5,b∈R}={x|x≥1},
故有M=P;
故选:A.
2.已知点P(sinπ,cosπ)落在角θ的终边上,且θ∈[0,2π),则θ的值为( )
A. B. C. D.
【考点】任意角的三角函数的定义.
【分析】解出点P的具体坐标,即可求解θ的值.
【解答】解:点P(sinπ,cosπ) 即P;
它落在角θ的终边上,且θ∈[0,2π),
∴
故选D.
3.一个几何体的三视图如图,则该几何体的体积为( )
A.π B. C. D.
【考点】由三视图求面积、体积.
【分析】由已知的三视图可得:该几何体是一个以俯视图为底面的半圆锥,代入锥体体积公式,可得答案.
【解答】解:由已知的三视图可得:该几何体是一个以俯视图为底面的半圆锥,
其底面面积S==,
高h=1,
故半圆锥的体积V==,
故选:D
4.执行如图的程序框图,则输出S的值为( )
A.2 B.﹣3 C. D.
【考点】程序框图.
【分析】根据已知的框图,可知程序的功能是利用循环计算S的值,并在循环变量k值大于等于2016时,输出累加结果.
【解答】解:模拟执行程序,可得
S=2,k=1,S=﹣3,
不满足条件k≥2016,k=2,S=﹣,
不满足条件k≥2016,k=3,S=,
不满足条件k≥2016,k=4,S=2,
不满足条件k≥2016,k=5,S=﹣3,
…
观察规律可知,S的取值周期为4,由于2016=504×4,可得
不满足条件k≥2016,k=2016,S=2,
满足条件k≥2016,满足退出循环的条件,
故输出的S值为2.
故选:A.
5.三个数a=30.7,b=0.73,c=log30.7的大小顺序为( )
A.b<c<a B.b<a<c C.c<a<b D.c<b<a
【考点】不等式比较大小.
【分析】由指数函数和对数函数的单调性,可得a,b,c的范围,进而可得答案.
【解答】解:∵a=30.7>30=1,
0<b=0.73<0.70=1,
c=log30.7<log31=0,
∴c<b<a.
故选D.
6.在等比数列{an}中,a2,a6是方程x2﹣34x+64=0的两根,则a4等于( )
A.8 B.﹣8 C.±8 D.以上都不对
【考点】函数的零点;等比数列的通项公式.
【分析】根据所给的等比数列的两项和方程根与系数的关系,求出a4的平方,根据条件中所给的三项都是偶数项,得出第四项是一个正数,得到结果.
【解答】解:∵a2,a6时方程x2﹣34x+64=0的两根,a2•a6=64,
∴a42=a2•a6=64
∴a4=±8
∵a4与a2,a6的符号相同,
a2+a4=34>0,
∴a4=8
故选A.
7.若l,m,n是不相同的空间直线,α,β是不重合的平面,则下列命题正确的是( )
A.α∥β,l⊂α,n⊂β⇒l∥n B B.l⊥n,m⊥n⇒l∥m
C.l⊥α,l∥β⇒α⊥β D.α⊥β,l⊂α⇒l⊥β
【考点】空间中直线与平面之间的位置关系.
【分析】运用面面平行、线面垂直的判定定理和性质定理对选项逐个分析判断.
【解答】解:对于A,α∥β,l⊂α,n⊂β⇒l∥n或者异面;故A错误;
对于B,l⊥n,m⊥n⇒l与m相交、平行或者异面;故B 错误;
对于C,由l∥β得到过直线l的平面与平面β交于直线a,则l∥a,由l⊥α,所以a⊥α,⇒α⊥β;故C正确;
对于D,α⊥β,l⊂α⇒l⊥β或者l∥β或者斜交;故D错误;
故选:C.
8.已知直线ax+2y+2=0与3x﹣y﹣2=0平行,则系数a=( )
A.﹣3 B.﹣6 C. D.
【考点】直线的一般式方程与直线的平行关系.
【分析】根据它们的斜率相等,可得﹣=3,解方程求a的值.
【解答】解:∵直线ax+2y+2=0与直线3x﹣y﹣2=0平行,
∴它们的斜率相等,
∴﹣=3
∴a=﹣6
故选:B.
9.有以下几种说法:(l1、l2不重合)
①若直线l1,l2都有斜率且斜率相等,则l1∥l2;
②若直线l1⊥l2,则它们的斜率互为负倒数;
③两条直线的倾斜角相等,则这两条直线平行;
④只有斜率相等的两条直线才一定平行.
以上说法中正确的个数是( )
A.1 B.2 C.3 D.0
【考点】命题的真假判断与应用.
【分析】利用直线的平行于斜率截距的关系判断命题的真假即可.
【解答】解:①若直线l1,l2都有斜率且斜率相等,l1∥l2;所以①正确;
②若直线l1⊥l2,则它们的斜率互为负倒数;显然必须两条直线的斜率存在的前提下是正确的;所以②不正确;
③两条直线的倾斜角相等,则这两条直线平行;正确;
④只有斜率相等的两条直线才一定平行.不正确;当两条直线的倾斜角是90°时,直线没有斜率,但是平行.
故选:B.
10.如图,在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
【考点】异面直线及其所成的角.
【分析】先通过平移将两条异面直线平移到同一个起点B,得到的锐角∠A1BC1就是异面直线所成的角,在三角形A1BC1中求出此角即可.
【解答】解:如图,连A1B、BC1、A1C1,则A1B=BC1=A1C1,
且EF∥A1B、GH∥BC1,
所以异面直线EF与GH所成的角等于60°,
故选B.
11.若直线y=kx+1与圆x2+y2+kx﹣y﹣9=0的两个交点恰好关于y轴对称,则k等于( )
A.0 B.1 C.2 D.3
【考点】直线和圆的方程的应用;直线与圆的位置关系.
【分析】判断直线与坐标轴的关系,然后判断直线与圆的位置关系即可.
【解答】解:直线y=kx+1与圆x2+y2+kx﹣y﹣9=0的两个交点恰好关于y轴对称,
可知k=0,
当k=0时,直线y=1与圆x2+y2﹣y﹣9=0,的两个交点(﹣3,0)和(3,0).
故选:A.
12.从直线x﹣y+3=0上的点向圆x2+y2﹣4x﹣4y+7=0引切线,则切线长的最小值为( )
A. B. C. D.﹣1
【考点】圆的切线方程.
【分析】由题意画出图形,求出圆心到直线x﹣y+3=0的距离,再由勾股定理求得切线长的最小值.
【解答】解:圆x2+y2﹣4x﹣4y+7=0化为(x﹣2)2+(y﹣2)2=1,
圆心为C(2,2),半径为1,如图,
直线x﹣y+3=0上的点向圆x2+y2﹣4x﹣4y+7=0引切线,要使切线长的最小,
则直线上的点与圆心的距离最小,
由点到直线的距离公式可得,|PC|=.
∴切线长的最小值为.
故选:B.
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上.)
13.若直线m被两平行直线l1:x﹣y+1=0,l2:x﹣y+3=0所截得的线段长为2,则m的倾斜角可以是 ①⑤ .
①15° ②30° ③45° ④60° ⑤75°.
【考点】两直线的夹角与到角问题.
【分析】利用两平行线间的距离公式求得两两平行线间的距离,设直线m与两平行直线的夹角为θ,根据 sinθ= 求得 θ=30°,由此可得直线m的倾斜角
【解答】解:两平行直线l1:x﹣y+1=0,l2:x﹣y+3=0之间的距离等于
=,设直线m与两平行直线的夹角为θ,
则有 sinθ==,∴θ=30°.
由于两平行直线的斜率为1,故它们的倾斜角等于45°,故m的倾斜角可以是 45°±30°,故m的倾斜角可以是75°或15°,
故答案为 ①⑤.
14.已知矩形ABCD中AB=3,BC=a,若PA⊥平面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有两个时,a的取值范围是 a>6 .
【考点】直线与平面垂直的性质;向量语言表述线线的垂直、平行关系.
【分析】以A点为原点,AB、AD、AP所在直线为x,y,z轴,建立空间直角坐标系,求出与的坐标,根据向量垂直数量积为零建立等量关系,使方程有两个不同的根即可求出a的值.
【解答】解:以A点为原点,AB、AD、AP所在直线为x,y,z轴,如图所示.
设P(0,0,b),D(0,a,0),E(3,x,0)
PE=(3,x,﹣b),DE=(3,x﹣a,0)
∵PE⊥DE,∴PE•DE=0,
∴9+x(x﹣a)=0,即x2﹣ax+9=0.
由题意可知方程有两个不同根,
∵△>0,即a2﹣4×9>0,∴a>6.
故答案为a>6
15.如图,半圆的直径AB=2,O为圆心,C为半圆上不同于A,B的任意一点,若P为半径OC上的动点,则的最小值是 ﹣ .
【考点】平面向量数量积的运算.
【分析】由向量的加法,可得,将其代入中,变形可得=﹣2(||﹣)2﹣,由二次函数的性质,计算可得答案.
【解答】解:根据题意,O为圆心,即O是AB的中点,则,
则≥﹣,
即的最小值是﹣;
故答案为﹣.
16.若x∈R,有意义且满足x2+y2﹣4x+1=0,则的最大值为 .
【考点】圆的一般方程;直线与圆的位置关系.
【分析】令则=k,则y=kx,代入x2+y2﹣4x+1=0,可得(1+k2)x2﹣4x+1=0,利用△=16﹣4(1+k2)≥0,可得结论.
【解答】解:令=k,则y=kx,代入x2+y2﹣4x+1=0,
可得(1+k2)x2﹣4x+1=0,△=16﹣4(1+k2)≥0,
∴,
∴的最大值为;
故答案为.
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)
17.圆x2+y2=8内有一点P0(﹣1,2),AB为过点P0且倾斜角为α的弦;
(1)当时,求AB的长;
(2)当弦AB被点P0平分时,求直线AB的方程.
【考点】直线和圆的方程的应用;直线的倾斜角;直线的一般式方程.
【分析】(1)根据直线的倾斜角求出斜率.因为直线AB过P0(﹣1,2),可表示出直线AB的解析式,利用点到直线的距离公式求出圆心到弦的距离,根据勾股定理求出弦的一半,乘以2得到弦AB的长;
(2)因为弦AB被点P0平分,先求出OP0的斜率,然后根据垂径定理得到OP0⊥AB,由垂直得到两条直线斜率乘积为﹣1,求出直线AB的斜率,然后写出直线的方程.
【解答】解:(1)直线AB的斜率k=tan=﹣1,
∴直线AB的方程为y﹣2=﹣(x+1),即x+y﹣1=0
∵圆心O(0,0)到直线AB的距离d==
∴弦长|AB|=2=2=.
(2)∵P0为AB的中点,OA=OB=r,
∴OP0⊥AB
又==﹣2,∴kAB=
∴直线AB的方程为y﹣2=(x+1),即x﹣2y+5=0
18.在△ABC中,a=3,b=2,∠B=2∠A.
(Ⅰ)求cosA的值;
(Ⅱ)求c的值.
【考点】正弦定理;余弦定理.
【分析】( I)由正弦定理得,结合二倍角公式及sinA≠0即可得解.
( II)由( I)可求sinA,又根据∠B=2∠A,可求cosB,可求sinB,利用三角形内角和定理及两角和的正弦函数公式即可得sinC,利用正弦定理即可得解.
【解答】解:( I)因为a=3,b=2,∠B=2∠A.
所以在△ABC中,由正弦定理得.
所以.
故.
( II)由( I)知,
所以.
又因为∠B=2∠A,
所以.
所以.
在△ABC中,.
所以.
19.如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
(1)求证:AC⊥BF;
(2)求证:BF⊥平面ACFD.
【考点】直线与平面垂直的判定;空间中直线与直线之间的位置关系.
【分析】(1)延长AD,BE,CF相交于一点K,推导出AC⊥BC,从而AC⊥平面BCK,由此能证明BF⊥AC.
(2)推导出△BCK为等边三角形,从而BF⊥CK,再由平面BCFE⊥平面ABC,∠ACB=90°,知AC⊥平面BCEF,从而BF⊥AC,由此能证明BF⊥平面ACFD.
【解答】(本小题满分12分)
证明:(1)延长AD,BE,CF相交于一点K,如图所示,
因为平面BCEF⊥平面ABC,且AC⊥BC,
所以AC⊥平面BCK,
因为BF⊂平面BCK,所以BF⊥AC. …
(2)因为EF∥BC,BE=EF=FC=1,BC=2,
所以△BCK为等边三角形,且F为CK的中点,
则BF⊥CK,
又平面BCFE⊥平面ABC,∠ACB=90°,
所以AC⊥平面BCEF,
因为BF⊂平面BCEF,所以BF⊥AC,
又AC∩CK=C,
所以BF⊥平面ACFD…..
20.已知数列{log2(an﹣1)}(n∈N*)为等差数列,且a1=3,a3=9.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明++…+<1.
【考点】等差数列的通项公式;等比数列的前n项和;不等式的证明.
【分析】(1)设等差数列{log2(an﹣1)}的公差为d.根据a1和a3的值求得d,进而根据等差数列的通项公式求得数列{log2(an﹣1)}的通项公式,进而求得an.
(2)把(1)中求得的an代入++…+中,进而根据等比数列的求和公式求得++…+=1﹣原式得证.
【解答】(I)解:设等差数列{log2(an﹣1)}的公差为d.
由a1=3,a3=9得2(log22+d)=log22+log28,即d=1.
所以log2(an﹣1)=1+(n﹣1)×1=n,即an=2n+1.
(II)证明:因为==,
所以++…+=+++…+==1﹣<1,
即得证.
21.如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N﹣BCM的体积.
【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.
【分析】(Ⅰ)取BC中点E,连结EN,EM,得NE是△PBC的中位线,推导出四边形ABEM是平行四边形,由此能证明MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,NF是△PAC的中位线,推导出NF⊥面ABCD,延长BC至G,使得CG=AM,连结GM,则四边形AGCM是平行四边形,由此能求出四面体N﹣BCM的体积.
【解答】证明:(Ⅰ)取BC中点E,连结EN,EM,
∵N为PC的中点,∴NE是△PBC的中位线
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN⊂平面NEM,∴MN∥平面PAB.
解:(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF==2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AMCG,∴四边形AGCM是平行四边形,
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=,
∴S△BCM===2,
∴四面体N﹣BCM的体积VN﹣BCM===.
22.已知圆C:x2+(y﹣1)2=5,直线l:mx﹣y+1﹣m=0.
(1)求证:对任意的m,直线l与圆C总有两个不同的交点;
(2)设l与圆C交于A,B两点,若|AB|=,求l的倾斜角;
(3)求弦AB的中点M的轨迹方程.
【考点】直线和圆的方程的应用.
【分析】(1)由直线系方程求得直线过定点,再由定点在圆内得结论;
(2)由弦长及圆的半径求得弦心距,再由圆心到直线的距离列式求得m的值,则直线l的倾斜角可求;
(3)设出弦AB的中点坐标,由直角三角形中的边长关系求得弦AB的中点M的轨迹.
【解答】(1)证明:由直线l:mx﹣y+1﹣m=0,得m(x﹣1)﹣y+1=0,
由,得.
∴直线l:mx﹣y+1﹣m=0过定点P(1,1),代入圆C:x2+(y﹣1)2=5,
得12+(1﹣1)2=1<5,∴点P(1,1)在圆C:x2+(y﹣1)2=5内部,
∴对任意的m,直线l与圆C总有两个不同的交点;
(2)解:当直线l的斜率不存在时,直线方程为x=1,代入圆x2+(y﹣1)2=5得:y1=﹣1,y2=3,
此时|AB|=4,不满足题意;
∴直线l的斜率存在,由|AB|=,圆的半径为,
得圆心到直线l:mx﹣y+1﹣m=0的距离为.
则,解得:.
∴直线l为或.
直线l的倾斜角为60°或120°;
(3)解:当M与P不重合时,连结CM、CP,则CM⊥MP,
∴|CM|2+|MP|2=|CP|2,
设M(x,y),则x2+(y﹣1)2+(x﹣1)2+(y﹣1)2=1,
化简得:x2+y2﹣x﹣2y+1=0(x≠1),
当M与P重合时,x=1,y=1也满足上式;
故弦AB中点的轨迹方程是x2+y2﹣x﹣2y+1=0.