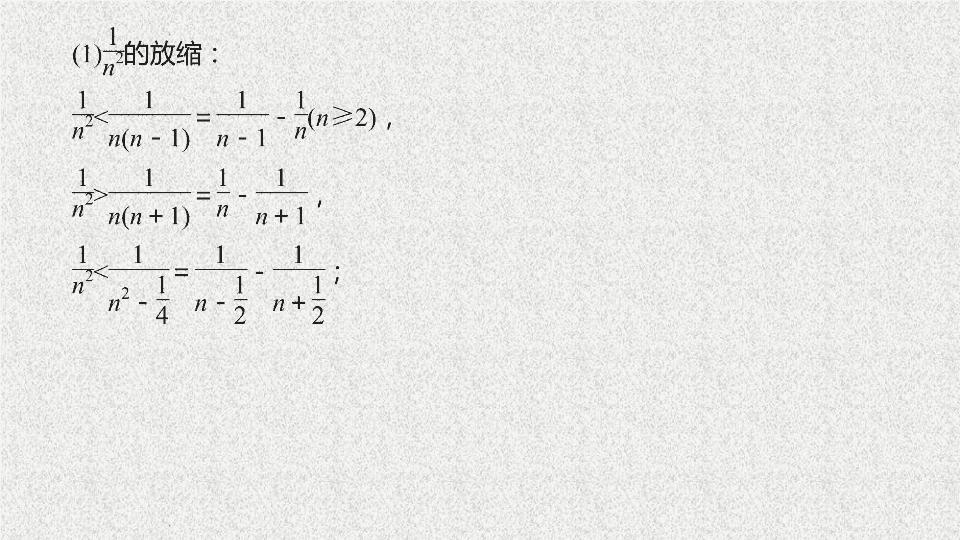2019届二轮复习放缩法在证明中的应用课件（13张）（全国通用） 13页

微专题七　放缩法在证明中的应用 第六章　 数列 [ 解题策略 ] 放缩法是不等式证明的重要方法，其中的放缩技巧既有模式可循但更有创意之变，如何灵活运用放缩法解题是衡量解题者思维好坏的标杆． 常见的放缩形式有： 另外，利用重要不等式放缩、导数应用中有关 ln x 型的放缩 ( 如： ln(1 ＋ x )< x ， x >0) 等也是常见的放缩方式． 利用放缩法证明不等式的难点是放缩的 “ 度 ” 不好把握，放大了或放小了都得不出所证不等式，这样需要回头调整，留一项或几项不放缩逐步试验向所证结论靠扰，下面举例说明． 又易知当 n ＝ 1 ， 2 ， 3 时，不等式显然成立．