【数学】2020届一轮复习人教A版立体几何中的向量方法课时作业 12页

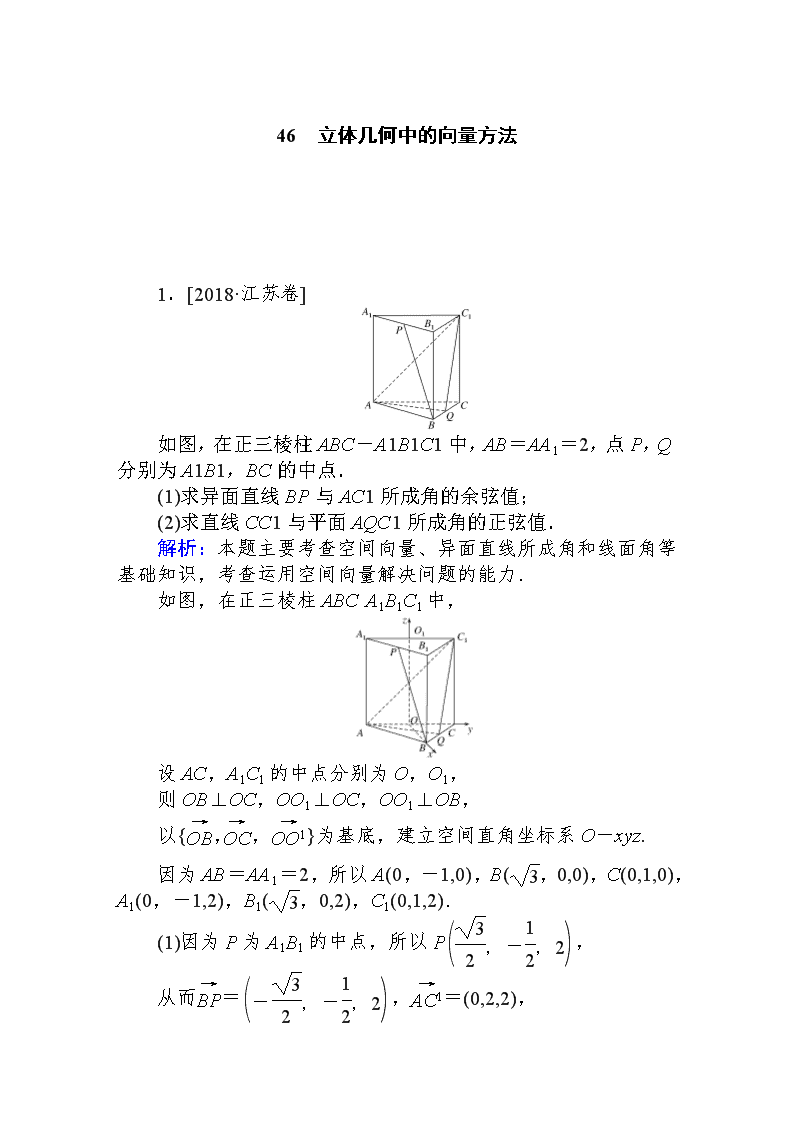
‎46　立体几何中的向量方法 ‎　　　　　　　　　　　　‎ ‎1．[2018·江苏卷]‎ 如图，在正三棱柱ABC－A1B1C1中，AB＝AA1＝2，点P，Q分别为A1B1，BC的中点．‎ ‎(1)求异面直线BP与AC1所成角的余弦值；‎ ‎(2)求直线CC1与平面AQC1所成角的正弦值．‎ 解析：本题主要考查空间向量、异面直线所成角和线面角等基础知识，考查运用空间向量解决问题的能力．‎ 如图，在正三棱柱ABCA1B1C1中，‎ 设AC，A1C1的中点分别为O，O1，‎ 则OB⊥OC，OO1⊥OC，OO1⊥OB，‎ 以{，，}为基底，建立空间直角坐标系O－xyz.‎ 因为AB＝AA1＝2，所以A(0，－1,0)，B(，0,0)，C(0,1,0)，A1(0，－1,2)，B1(，0,2)，C1(0,1,2)．‎ ‎(1)因为P为A1B1的中点，所以P，‎ 从而＝，＝(0,2,2)，‎ 故|cos〈，〉|＝＝＝.‎ 因此，异面直线BP与AC1所成角的余弦值为.‎ ‎(2)因为Q为BC的中点，所以Q，因此＝，＝(0,2,2)，＝(0,0,2)．‎ 设n＝(x，y，z)为平面AQC1的一个法向量，‎ 则即 不妨取n＝(，－1,1)．‎ 设直线CC1与平面AQC1所成角为θ，‎ 则sin θ＝|cos〈，n〉|＝＝＝，所以直线CC1与平面AQC1所成角的正弦值为.‎ ‎2．[2019·郑州一中入学测试]在如图所示的多面体中，四边形ABCD是平行四边形，四边形BDEF是矩形，ED⊥平在ABCD，∠ABD＝，AB＝2AD.‎ ‎(1)求证：平面BDEF⊥平面ADE；‎ ‎(2)若ED＝BD，求直线AF与平面AEC所成角的正弦值．‎ 解析：(1)在△ABD中，∠ABD＝，AB＝2AD，‎ 由余弦定理，得BD＝AD，‎ 从而BD2＋AD2＝AB2，故BD⊥AD，‎ 所以△ABD为直角三角形且∠ADB＝90°.‎ 因为DE⊥平面ABCD，BD⊂平面ABCD，所以DE⊥BD.‎ 又AD∩DE＝D，所以BD⊥平面ADE.‎ 因为BD⊂平面BDEF，所以平面BDEF⊥平面ADE.‎ ‎(2)由(1)可得，在Rt△ABD中，∠BAD＝，BD＝AD，又由ED＝BD，‎ 设AD＝1，则BD＝ED＝.因为DE⊥平面ABCD，BD⊥AD，‎ 所以可以点D为坐标原点，DA，DB，DE所在直线分别为x轴，y轴，z轴建立空间直角坐标系，如图所示D－xyz.‎ 则A(1,0,0)，C(－1，，0)，E(0,0，)，F(0，，)，‎ 所以＝(－1,0，)，＝(－2，，0)．‎ 设平面AEC的法向量为n＝(x，y，z)，‎ 则即 令z＝1，得n＝(，2,1)，为平面AEC的一个法向量．‎ 因为＝(－1，，)，‎ 所以cos〈n，〉＝＝.‎ 所以直线AF与平面AEC所成角的正弦值为.‎ ‎3．[2019·石家庄摸底考试]如图，在多面体ABCDPE中，四边形ABCD和CDPE都是直角梯形，AB∥DC，PE∥DC，AD⊥DC，‎ PD⊥平面ABCD，AB＝PD＝DA＝2PE，CD＝3PE，F是CE的中点．‎ ‎(1)求证：BF∥平面ADP；‎ ‎(2)求二面角B－DF－P的余弦值．‎ 解析：(1)取PD的中点为G，连接FG，AG，如图所示，‎ ‎∵F是CE的中点，∴FG是梯形CDPE的中位线，‎ ‎∵CD＝3PE，∴FG＝2PE，‎ ‎∵FG∥CD∥AB，AB＝2PE，‎ ‎∴AB∥FG，AB＝FG，即四边形ABFG是平行四边形，‎ ‎∴BF∥AG，‎ 又BF⊄平面ADP，AG⊂平面ADP，∴BF∥平面ADP.‎ ‎(2)解法一　∵PD⊥平面ABCD，∴PD⊥AD，又AD⊥DC，且PD∩CD＝D，∴AD⊥平面CDPE.‎ 过点B作BM⊥CD于点M，易知BM∥AD，‎ ‎∴BM⊥平面CDPE.令PE＝1，则BM＝DM＝2，连接FM，‎ 由(1)易得FM＝1，‎ 如图，过点M作MN⊥DF交DF于点N，连接BN，则∠BNM为所求二面角的平面角的补角．‎ ‎∵DM＝2，FM＝1，‎ ‎∴DF＝，则MN＝.‎ ‎∴tan∠BNM＝＝，则cos∠BNM＝，‎ ‎∴二面角B－DF－P的余弦值为－.‎ 解法二　∵PD⊥平面ABCD，∴PD⊥AD，‎ 又AD⊥DC，且PD∩DC＝D，‎ ‎∴AD⊥平面CDPE.‎ 以D为坐标原点，DA，DC，DP所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系D－xyz，设PE＝1，‎ 则A(2,0,0)，B(2,2,0)，C(0,3,0)，D(0,0,0)，P(0,0，2)，E(0,1,2)，F(0,2,1)，‎ ‎∴＝(2,2,0)，＝(0,2,1)，‎ 设平面BDF的法向量为n＝(x，y，z)，‎ 则即 令y＝－1，则x＝1，z＝2，‎ ‎∴n＝(1，－1,2)，为平面BDF的一个法向量．‎ ‎∵平面PDF的一个法向量为＝(2,0,0)，且二面角B－DF－P的平面角为钝角，‎ ‎∴二面角B－DF－P的余弦值为－|cos〈，n〉|＝－.‎ ‎4．[2019·唐山模拟]如图，在四棱锥P－ABCD中，PC⊥底面ABCD，ABCD是直角梯形，AB⊥AD，AB∥CD，AB＝2AD＝2CD，E是PB的中点．‎ ‎(1)求证：平面EAC⊥平面PBC；‎ ‎(2)若二面角P－AC－E的余弦值为，求直线PA与平面EAC所成角的正弦值．‎ 解析：(1)因为PC⊥平面ABCD，AC⊂平面ABCD，所以AC⊥PC.‎ 因为AB＝2AD＝2CD，所以AC＝BC＝AD＝CD.‎ 所以AC2＋BC2＝AB2，故AC⊥BC.‎ 又BC∩PC＝C，所以AC⊥平面PBC.‎ 因为AC⊂平面EAC，所以平在EAC⊥平面PBC.‎ ‎(2)如图，以C为原点，，，的方向分别为x轴、y轴、z轴的正方向，建立空间直角坐标系C－xyz，并设CB＝2，CP＝2a(a>0)．则C(0,0,0)，A(0,2,0)，B(2,0,0)，P(0,0,2a)，‎ 则E(1,0，a)，‎ ＝(0,2,0)，＝(0,0,2a)，＝(1,0，a)，‎ 易知m＝(1,0,0)为平面PAC的一个法向量．‎ 设n＝(x，y，z)为平面EAC的法向量，则n·＝n·＝0，‎ 即y＝0，取x＝a，则z＝－1，n＝(a,0，－1)．‎ 依题意，|cos〈m，n〉|＝＝＝，则a＝.‎ 于是n＝(，0，－1)，＝(0,2，－2)．‎ 设直线PA与平面EAC所成角为θ，‎ 则sinθ＝|cos〈，n〉|＝＝，‎ 即直线PA与平面EAC所成角的正弦值为.‎ ‎5．[2018·天津卷]‎ 如图，AD∥BC且AD＝2BC，AD⊥CD，EG∥AD且EG＝‎ AD，CD∥FG且CD＝2FG，DG⊥平面ABCD，DA＝DC＝DG＝2.‎ ‎(1)若M为CF的中点，N为EG的中点，求证：MN∥平面CDE；‎ ‎(2)求二面角E－BC－F的正弦值；‎ ‎(3)若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长．‎ 解析：‎ 本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识．考查用空间向量解决立体几何问题的方法．考查空间想象能力、运算求解能力和推理论证能力．‎ 依题意，可以建立以D为原点，分别以，，的方向为x轴，y轴，z轴的正方向的空间直角坐标系D－xyz(如图)，可得D(0,0,0)，A(2,0,0)，B(1,2,0)，C(0，2,0)，E(2,0,2)，F(0,1,2)，G(0,0,2)，M，N(1,0,2)．‎ ‎(1)证明：依题意＝(0,2,0)，＝(2,0,2)．‎ 设n0＝(x0，y0，z0)为平面CDE的法向量，则即 不妨令z0＝－1，可得n0＝(1,0，－1)．‎ 又＝，可得·n0＝0，‎ 又因为直线MN⊄平面CDE，‎ 所以MN∥平面CDE.‎ ‎(2)依题意，可得＝(－1,0,0)，＝(1，－2,2)，＝(0，－1,2)．‎ 设n＝(x1，y1，z1)为平面 BCE的法向量，‎ 则即 不妨令z1＝1，可得n＝(0,1,1)．‎ 设m＝(x2，y2，z2)为平面BCF的法向量，‎ 则即 不妨令z2＝1，可得m＝(0,2,1)．‎ 因此有cos〈m，n〉＝＝，于是sin〈m，n〉＝.‎ 所以，二面角E－BC－F的正弦值为.‎ ‎(3)设线段DP的长为h(h∈[0,2])，则点P的坐标为(0,0，h)，可得＝(－1，－2，h)．‎ 易知，＝(0,2,0)为平面ADGE的一个法向量，‎ 故|cos〈，〉|＝＝，‎ 由题意，可得＝sin 60°＝，解得h＝∈[0,2]．‎ 所以，线段DP的长为.‎ ‎6．[2019·山西八校联考]如图，三棱柱ABC－A1B1C1中，∠ACB＝90°，CC1⊥底面ABC，AC＝BC＝CC1＝2，D，E，F分别是棱AB，BC，B1C1的中点，G是棱BB1上的动点．‎ ‎(1)当为何值时，平面CDG⊥平面A1DE?‎ ‎(2)求平面A1BF与平面A1DE所成的锐二面角的余弦值．‎ 解析：(1)当G为BB1的中点，即＝时，平面CDG⊥平面A1DE.‎ 证明如下：因为点D，E分别是AB，BC的中点，所以DE∥AC且DE＝AC，又AC∥A1C1，AC＝A1C1，所以DE∥A1C1，DE＝A1C1，故D，E，C1，A1四点共面．‎ 如图，连接C1E交GC于H.在正方形CBB1C1中，tan∠C1EC＝2，tan∠BCG＝，故∠CHE＝90°，即CG⊥C1E.因为A1C1⊥平面CBB1C1，CG⊥平面CBB1C1，所以DE⊥CG，又C1E∩DE＝E，所以CG⊥平面A1DE，故平面CDG⊥平面A1DE.‎ ‎(2)三棱柱ABC－A1B1C1中，∠ACB＝90°，CC1⊥底面ABC，所以以C为原点，CA，CB，CC1所在的直线分别为x轴，y轴，z轴建立空间直角坐标系C－xyz，如图所示．‎ 因为AC＝BC＝CC1＝2，D，E，F分别是棱AB，BC，B1C1的中点，‎ 所以C(0,0,0)，A1(2,0,2)，D(1,1,0)，E(0,1,0)，B(0,2,0)，F(0,1,2)，G(0,2,1)，＝(－2,2，－2)，＝(－2,1,0)， ‎＝(0,2,1)．‎ 由(1)知平面A1DE的一个法向量为＝(0,2,1)，‎ 设平面A1BF的法向量为n＝(x，y，z)，‎ 则即 令x＝1得n＝(1,2,1)，为平面A1BF的一个法向量．‎ 设平面A1BF与平面A1DE所成的锐二面角为θ，‎ 则cosθ＝＝＝，‎ 所以平面A1BF与平面A1DE所成的锐二面角的余弦值为.‎ ‎7．[2019·湖北四校联考]如图，已知直三棱柱ABC－A1B1C1中，AA1＝AB＝AC＝1，AB⊥AC，M，N，Q分别是CC1，BC，AC的中点，点P在直线A1B1上运动，且＝λ(λ∈[0,1])．‎ ‎(1)证明：无论λ取何值，总有AM⊥平面PNQ；‎ ‎(2)是否存在点P，使得平面PMN与平面ABC的夹角为60°？若存在，试确定点P的位置，若不存在，请说明理由．‎ 解析：(1)连接A1Q.‎ ‎∵AA1＝AC＝1，M，Q分别是CC1，AC的中点，‎ ‎∴△AA1Q≌△CAM，‎ ‎∴∠MAC＝∠QA1A，‎ ‎∴∠MAC＋∠AQA1＝∠QA1A＋∠AQA1＝90°，∴AM⊥A1Q.‎ ‎∵N，Q分别是BC，AC的中点，∴NQ∥AB.‎ 又AB⊥AC，∴NQ⊥AC.‎ 在直三棱柱ABC－A1B1C1中，AA1⊥底面ABC，∴NQ⊥AA1.‎ 又AC∩AA1＝A，∴NQ⊥平面ACC1A1，‎ ‎∴NQ⊥AM.‎ 由NQ∥AB和AB∥A1B1可得NQ∥A1B1，‎ ‎∴N，Q，A1，P四点共面，‎ ‎∴A1Q⊂平面PNQ.‎ ‎∵NQ∩A1Q＝Q，∴ AM⊥平面PNQ，∴无论λ取何值，总有AM⊥平面PNQ.‎ ‎(2)如图，以A为坐标原点，AB，AC，AA1所在的直线分别为x轴，y轴，z轴建立空间直角坐标系A－xyz，‎ 则A1(0,0,1)，B1(1,0,1)，M，N，Q，＝，＝(1,0,0)．由＝λ＝λ(1,0,0)＝(λ，0,0)，可得点P(λ，0,1)，‎ ‎∴＝.‎ 设n＝(x，y，z)是平面PMN的法向量，‎ 则 即得 令x＝3，得y＝1＋2λ，z＝2－2λ，∴n＝(3,1＋2λ，2－2λ)是平面PMN的一个法向量．‎ 取平面ABC的一个法向量为m＝(0,0,1)．‎ 假设存在符合条件的点P，则|cos〈m，n〉|＝＝，化简得4λ2－14λ＋1＝0，解得λ＝或λ＝(舍去)．‎ 综上，存在点P，且当A1P＝时，满足平面PMN与平面ABC的夹角为60°.‎