福建省2020届高三考前冲刺适应性模拟卷（二）数学（文）试题 Word版含解析 24页

- 1 - 福建省 2020 届高三数学考前冲刺适应性模拟卷 文科数学（二） 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．本试卷共 4 页，满分 150 分．考 试时间 120 分钟 第Ⅰ卷 一.选择题：本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 1.已知全集  1,2,3,4,5U＝ ，集合 A＝{ | 3 2}x Z x   ,则集合 CuA 等于 A.  1,2,3,4 B.  2,3,4 C.  1,5 D.  5 【答案】C 【解析】 【分析】 先求解集合 A，再求补集即可. 【详解】由 A＝  { | 3 2} 2,3,4x Z x    ，全集  1,2,3,4,5U＝ ， 所以 CuA  1,5 . 故选 C. 【点睛】本题主要考查了集合补集的求解，属于基础题. 2.欧拉公式 cos sinixe x i x  （i 为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数 函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常 重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知， 2ie 表示的复数在复平面中位于 （ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】C 【解析】 【分析】 根据定义化简 2ie ，再根据复数几何意义确定结果. - 2 - 【详解】 2cos sin cos( 2) sin( 2)ix ie x i x e i      Q 对应点坐标为 (cos( 2),sin( 2))  2 ( , ) cos( 2) cos2 0,sin( 2) sin 2 02          Q 因此 2ie 表示的复数在复平面中位于第三象限， 故选：C 【点睛】本题考查新定义、复数几何意义、三角函数符号规律，考查基本分析求解能力，属 基础题. 3.“直线 : 2 1l y kx k   在坐标轴上截距相等”是“ 1k   ”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 【答案】B 【解析】 【分析】 由直线 : 2 1l y kx k   在坐标轴上截距相等得 1 2k  或 1k   ，再根据充分条件和必要条件 的定义判断即可. 【详解】解：由题知： 0k  ，由 0x  得 2 1y k  ；由 0y  得， 1 2kx k  . 因为在坐标轴上的截距相等，所以 1 22 1 kk k   ，解得 1 2k  或 1k   . 所以直线 : 2 1l y kx k   在坐标轴上截距相等”是“ 1k   ”的必要不充分条件. 故选：B. 【点睛】本题主要考查直线的截距与充分条件、必要条件，属于基础题. 4.在等差数列{ }na 中， 9 12 1 62a a  ，则{ }na 的前11项和 11S  （ ） A. 132 B. 66 C. 48 D. 24 【答案】A 【解析】 设 等 差 数 列  na 的 公 差 为 d ， 因 为 9 12 1 62a a  ， 所 以  1 1 18 11 62a d a d    ， 1 5 12a d  ， 6 12a  ，  1 11 11 6 11 11 1322 a aS a    ，故选 A. 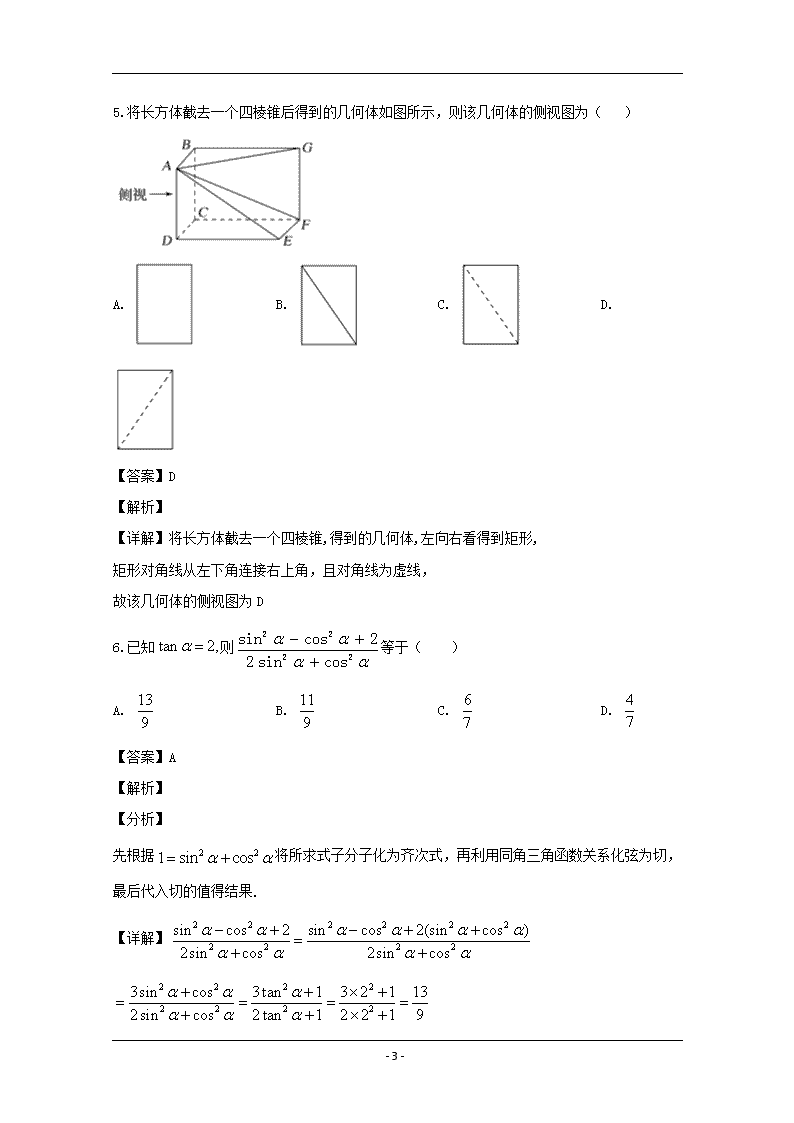- 3 - 5.将长方体截去一个四棱锥后得到的几何体如图所示，则该几何体的侧视图为（ ） A. B. C. D. 【答案】D 【解析】 【详解】将长方体截去一个四棱锥,得到的几何体,左向右看得到矩形, 矩形对角线从左下角连接右上角，且对角线为虚线， 故该几何体的侧视图为 D 6.已知 tan 2,  则 2 2 2 2 sin cos 2 2 sin cos        等于（ ） A. 13 9 B. 11 9 C. 6 7 D. 4 7 【答案】A 【解析】 【分析】 先根据 2 21 sin cos   将所求式子分子化为齐次式，再利用同角三角函数关系化弦为切， 最后代入切的值得结果. 【详解】 2 2 2 2 2 2 2 2 2 2 sin cos 2 sin cos 2(sin cos ) 2sin cos 2sin cos                 2 2 2 2 2 2 2 2 3sin cos 3tan 1 3 2 1 13 2sin cos 2tan 1 2 2 1 9                 - 4 - 故选：A 【点睛】本题考查同角三角函数关系、弦为切，考查基本分析求解能力，属基础题. 7.已知向量 a ，b 满足 1a  ， 3b  ， 2 + 7a b  ，则 b 与 a b  的夹角为（ ） A. 30° B. 60 C. 120 D. 150 【答案】D 【解析】 【分析】 将 2 + 7a b  两边平方求得 0a b  ，再计算出 2a b  ，利用向量的夹角公式可得选项. 【详解】将 2 + 7a b  两边平方得 2 24 +4 + 7a a b b    ，所以 0a b  ， 又 2 2 22 + 4ba ba b a       ，所以 2a b  ， 设b 与 a b  的夹角为 ，则   2 3cos 23 2 b a b a b b a b b                ， 又 0    ，所以 150   , 故选：D. 【点睛】本题考查向量的数量积运算，向量的模，向量的夹角的计算，求解向量的夹角时， 注意向量的夹角的范围，属于中档题. 8.   2 ln xf x x x   ，则函数  y f x 的大致图像为（ ） A. B. C. D. 【答案】A 【解析】 【分析】 根据绝对值定义将函数化为分段函数，利用导数判断 0x  单调性舍去 CD,再根据  1f  为正 - 5 - 舍去 B，即可得结果. 【详解】   2 2 2 ln , 0ln ln( ) , 0 xx xx xf x x xx x xx           所以当 0x  时，   3 2 2 1 ln 2 1 ln2 x x xf x x x x       ， 令 3 2 1( ) 2 1 ln ( ) 6 0g x x x g x x x        0 02 1 2 1(1) 1 0, ( ) 2 0 ( ,1), ( ) 0g g x g xe e e        Q 所以当 0(0, )x x 时， ( ) 0, ( ) 0g x f x   ；当 0( , )x x  时， ( ) 0, ( ) 0g x f x   ；舍去 C,D; 当 0x  时，  1 1 0f    ，舍去 B; 故选：A 【点睛】本题考查函数图象识别、利用导数研究函数单调性，考查基本分析判断能力，属基础 题. 9.已知  2 2log 2 17y x x   的值域为 ,m  ，当正数 a，b 满足 2 1 3 2 ma b a b    时， 则 7 4a b 的最小值为（ ） A. 9 4 B. 5 C. 5 2 2 4  D. 9 【答案】A 【解析】 【分析】 利用  2 2log 2 17y x x   的值域为  ,m  ,求出 m,再变形,利用 1 的代换,即可求出 7 4a b 的最小值. 【详解】解：∵    22 2 2log 2 17 log 1 16y x x x        的值域为 ,m  , ∴ 4m  , ∴ 4 1 46 2 2a b a b    , ∴    1 4 17 4 6 2 24 6 2 2a b a b a b a b a b              - 6 -    4 21 6 2 1 95 5 44 2 6 2 4 4 a ba b a b a b            , 当且仅当  4 26 2 2 6 2 a ba b a b a b    时取等号, ∴ 7 4a b 的最小值为 9 4 . 故选：A. 【点睛】本题主要考查了对数复合函数的值域运用,同时也考查了基本不等式中“1 的运用”, 属于中档题. 10.已知圆 C： 2 2 2 1 0x y x    ，直线 :3 4 12 0l x y   ，圆 C 上任意一点 P 到直线l 的距 离小于 4 的概率为（ ） A. 1 3 B. 2 3 C. 3 4 D. 1 4 【答案】C 【解析】 【分析】 先将圆方程化为标准形式，求出圆心到直线l 的距离，然后确定圆上到直线l 的距离为 4 的点 ,A B ，求出弦 AB 对应的圆心角，最后根据几何概型得出所求概率. 【详解】圆 2 2: 2 1 0C x y x    ，即 2 2( 1) 2x y   ， 故圆C 的圆心为 (1,0)C ，半径为 2 ， 则圆心 (1,0)C 到直线 :3 4 12 0l x y   的距离 3 12 35d   ， 如图所示，设圆上 ,A B 两点到直线l 的距离为 4 ， - 7 - 则优弧 AB 上的点到直线 l 的距离小于 4， 设 D 为 AB 的中点，则 1CD  ，所以 2 2 2 1 2AB AD    ， 所以 2 2 2AB AC BC  ，即 90ACB   , 所以圆C 上任意一点到直线 l 的距离小于 4 的概率为 360 90 3 360 4      ， 故选：C. 【点睛】本题结合了直线与圆的相关知识，考查了几何概型概率的求法，需要学生具备一定 的计算分析能力，综合性较强. 11.点 P 在以 F 为焦点的抛物线 2 4x y 上， 5PF  ，以 P 为圆心， PF 为半径的圆交 x 轴 于 ,A B 两点，则 AP AB   （ ） A. 9 B. 12 C. 18 D. 32 【答案】C 【解析】 【分析】 先由题意求出点 P 坐标，得到以 P 为圆心， PF 为半径的圆的方程，求出 ,A B 两点坐标，根 据向量数量积的坐标表示，即可计算出结果. 【详解】设  0 0,P x y ， 因为抛物线 2 4x y 的焦点为  0,1F ， 5PF  ， 所以 0 1 5y   ，即 0 4y  ，因此 2 0 04 16x y  ，解得： 0 4x   ，不妨取 0 4x  ， 则  4,4P ， 因此以 P 为圆心， PF 为半径的圆的方程为：   2 24 4 25x y    ， 令 0y  ，解得： 7x  或 1x  ，即圆   2 24 4 25x y    与 x 轴的两交点为  7,0 ， 1,0 ， 不妨取  7,0A ，  10B , ， 则  3,4AP   ，  6,0AB   ， 因此 18AP AB   . - 8 - 故选：C. 【点睛】本题主要考查求向量的数量积，涉及由抛物线的焦半径求点的坐标问题，熟记向量 数量积的坐标公式，以及抛物线的简单性质即可，属于常考题型. 12.已知函数   2g x a x  （ 1 x ee   ， e 为自然对数的底数）与   2lnh x x 的图象上存 在关于 x 轴对称的点，则实数 a 的取值范围是（） A. 2 11, 2e     B. 21, 2e   C. 2 2 1 2, 2ee      D. 2 2,e   【答案】B 【解析】 【分析】 设  0 0,2lnM x x ， 0 1 x ee   ，且其关于 x 轴对称点 M  在  g x 上；将 M  坐标代入  g x ， 可 得 2 0 0 12lnx x a x ee        ， 从 而 将 问 题 转 化 为 此 方 程 有 解 ； 令   2 12lnf x x x x ee        ，通过导数可确定函数的大致图象，将问题转化为 y a 与  y f x 图象有交点，通过数形结合求得结果. 【 详 解 】 设  h x 上 一 点  0 0,2lnM x x ， 0 1 x ee   ， 且 M 关 于 x 轴 对 称 点 坐 标 为  0 0, 2lnM x x  ， 0 1 x ee   在  g x 上 2 0 0 12ln x a x x ee         ，有解，即 2 0 0 12lnx x a x ee        有解 令   2 12lnf x x x x ee        ，则     2 1 122 x xf x x x x      ， 1 x ee   当 1 ,1x e     时，   0f x  ；当  1,x e 时，   0f x   f x 在 1 ,1e     上单调递减；在 1,e 上单调递增 - 9 -    min 1 1f x f   ， 2 1 1 2f e e       ，   2 2f e e  可得  f x 图象如下图所示： 2 0 0 12lnx x a x ee        有解等价于 y a 与  y f x 图象有交点    1f a f e   21, 2a e     本题正确选项： B 【点睛】本题考查根据方程有根求解参数范围的问题；关键是能够根据对称性将问题转化为 方程有根，通过构造函数的方式进一步将问题转化为平行于 x 轴直线与曲线有交点的问题，进 而通过数形结合的方式来进行求解. 第Ⅱ卷 本卷包括必考题和选考题两部分.第    13 ~ 21 题为必考题，每个试题考生都必须做答.第    22 23、 题为选考题，考生根据要求做答. 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分） 13.下图是一个算法流程图，则输出 S 的值是___________． - 10 - 【答案】35 【解析】 【分析】 按照程序框图的流程，写出前几次循环的结果，并判断每个结果是否满足判断框中的条件， 直到满足条件，输出结论． 【详解】S 的初值为 0，K 的初值为 1，满足进行循环的条件， 经过第一次循环得到的结果为 S＝1，K＝3，不满足条件，进行循环， 经过第二次循环得到的结果为 S＝10，K＝5，不条件满足，进行循环， 经过第三次循环得到的结果为 S＝35，K＝7，满足条件，退出循环， 故输出的 S 值为 35. 故答案为：35. 【点睛】本题考查执行程序框图问题，属于中档题.在解决程序框图问题时一定注意以下几点： (1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注 意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次 数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框 图规定的运算方法逐次计算，直到达到输出条件即可. 14.点 P 在双曲线 2 2 12 x y  上，点Q 在曲线  22 3 4x y   上，线段 PQ 的中点为 M ，O 是坐标原点，则线段OM 长的最小值是________． - 11 - 【答案】 2 1 【解析】 【分析】 设 1 1( , )P x y ， 2 2( , )Q x y ，取 P 关于原点的对称点 1 1 1( , )P x y  ，则 1 1| | | |2OM PQ ，根据 1 1| | | | 2PQ PN  ，根据两点间的距离公式求出 1| |PN 的最小值即可得答案. 【详解】 设 1 1( , )P x y ， 2 2( , )Q x y ，取 P 关于原点的对称点 1 1 1( , )P x y  ，所以 2 21 1 ( ) ( ) 12 x y    ， 即 2 2 1 12 2x y  ， 则 1 1| | | |2OM PQ ， 因为 1 1| | | | 2PQ PN  2 2 1 1( 0) ( 3) 2x y       2 2 1 1 16 9 2x y y     2 1 13 6 11 2y y    2 13( 1) 8 2y    2 2 2≥ ，当且仅当 1 1y   时，取等号， 所以| | 2 1OM   ，即| |OM 的最小值为 2 1 . 故答案为： 2 1 . 【点睛】本题考查了双曲线方程和圆的方程，考查了运算求解能力，属于中档题. 15.半径为 1 的球面上有四个点 , , ,A B C D ，球心为点 O ，AB 过点O ，CA CB ，DA DB ， 1DC  ，则三棱锥 A BCD 的体积为______. - 12 - 【答案】 3 6 【解析】 【分析】 连结 ,OC OD ，易知 ,AB OD AB OC  ，从而可证明 AB  平面 OCD ，进而三棱锥 A BCD 的体积 1 3 OCDV S AB  ，然后求出 OCDS 和 AB 即可. 【详解】连结 ,OC OD ，因为CA CB ， DA DB ，O 为 AB 的中点， 所以 ,AB OD AB OC  ， 又因为OC OD O ，所以 AB  平面 OCD ， 因为 1OC OD DC   ，所以 1 3 31 12 2 4OCDS      ， 所以三棱锥 A BCD 的体积 1 1 1 3 3 3OCD OCD OCDV S OA S OB S AB        1 3 323 4 6     . 故答案为： 3 6 . 【点睛】本题考查三棱锥体积的求法，考查球的内接体知识，考查学生的空间想象能力与计 算求解能力，属于中档题. 16.已知函数 2 ln , 0( ) 4 1, 0 x xf x x x x       ，若关于 x 的方程 2 ( ) ( ) 0( , )f x bf x c b c R    有 8 个不同的实数根，则 2 1   c b 的取值范围为________________ 【答案】   , 1 2,   - 13 - 【解析】 【详解】根据题意作出 f(x)的简图： 由图象可得当 f(x)∈(0,1]时,有四个不同的 x 与 f(x)对应． 再结合题中“方程 f2(x)−bf(x)+c=0 有 8 个不同实数解”， 可以分解为形如关于 k 的方程 k2−bk+c=0 有两个不同的实数根 K1、K2， 且 K1 和 K2 均为大于 0 且小于等于 1 的实数， 列式如下： 2 2 2 4 0 0 12 0 0 0 1 0 b c b b c b c               … ,化简得 2 4 1 0 0 0 2 bc b c c b           ， 此不等式组表示的区域如图： 而 2 1   c b 几何意义表示平面区域内的点和(1,2)的直线的斜率， 结合图象 KOA=2,KAB=−1， 故 z>2 或 z<−1， 故答案为(−∞,−1)∪(2,+∞). 点睛：(1)本题是线性规划的综合应用，考查的是非线性目标函数的最值的求法． - 14 - (2)解决这类问题的关键是利用数形结合的思想方法，给目标函数赋于一定的几何意义． 三、解答题（本大题共 70 分.解答应写出文字说明，证明过程或演算步骤） 17.已知函数 ( ) sin 2 cos ( 0)f x m x x m   的最大值为 2． （1）求函数 ( )f x 在 0, 上的单调递减区间． （2） ABC 中，若角 , ,A B C 所对的边分别是 , ,a b c 且满足 60C   ， 边 3c  ，及 ( ) ( ) 4 6 sin sin4 4f A f B A B     ,求 ABC 的面积． 【答案】（1） 0 4      ， ；（2） 3 3.4 【解析】 【分析】 （1）将 f（x）解析式利用两角和与差的正弦函数公式化为一个角的正弦函数，由正弦函数的 值域表示出 f（x）的最大值，由已知最大值为 2 列出关于 m 的方程，求出方程的解得到 m 的 值，进而确定出 f（x）的解析式，由正弦函数的递减区间为[2kπ+ 2  ，2kπ+ 3 2  ]（k∈Z）， 列出关于 x 的不等式，求出不等式的解集即可得到 f（x）在[0，π]上的单调递减区间；（2） 由（1）确定的 f（x）解析式化简 f（A﹣ 4  ）+f（B﹣ 4  ）=4 6 sinAsinB，再利用正弦定理 化简，得出 a+b= 2 ab①，利用余弦定理得到（a+b）2﹣3ab﹣9=0②，将①代入②求出 ab 的 值，再由 sinC 的值，利用三角形的面积公式即可求出三角形 ABC 的面积． 【详解】（1）f（x）=msinx+ cosx= sin（x+θ）（其中 sinθ= ，cosθ= ）， ∴f（x）的最大值为 ， ∴ =2， 又 m＞0，∴m= ， ∴f（x）=2sin（x+ ）， 令 2kπ+ ≤x+ ≤2kπ+ （k∈Z），解得：2kπ+ ≤x≤2kπ+ （k∈Z）， 则 f（x）在[0，π]上的单调递减区间为[ ，π]； - 15 - （2）设△ABC 的外接圆半径为 R，由题意 C=60°，c=3，得 = = = =2 ， 化简 f（A﹣ ）+f（B﹣ ）=4 sinAsinB，得 sinA+sinB=2 sinAsinB， 由正弦定理得： + =2 × ，即 a+b= ab①， 由余弦定理得：a2+b2﹣ab=9，即（a+b）2﹣3ab﹣9=0②， 将①式代入②，得 2（ab）2﹣3ab﹣9=0， 解得：ab=3 或 ab=﹣ （舍去）， 则 S△ABC= absinC= ． 【点睛】此题考查了正弦、余弦定理，三角形的面积公式，两角和与差的正弦函数公式，以 及正弦函数的单调性，熟练掌握定理及公式是解本题的关键．对余弦定理一定要熟记两种形 式：（1） 2 2 2 2 cosa b c bc A   ；（2） 2 2 2 cos 2 b c aA bc   ，同时还要熟练掌握运用两种形 式的条件.另外，在解与三角形、三角函数有关的问题时，还需要记住 30 ,45 ,60o o o 等特殊角 的三角函数值，以便在解题中直接应用. 18.如图，在三棱柱 1 1 1ABC A B C 中，已知 AB ⊥侧面 1 1BBC C ， 1AB BC  1 2BB  ， 1 3BCC   ． （1）求证： 1C B  平面 ABC ； （2）求点 B 到平面 1 1ABC 的距离． 【答案】（1）证明见解析；（2） 3 2 ． - 16 - 【解析】 试题分析：（1）由 1 1AB BB C C 得出 1AB BC ,利用余弦定理算出 1BC ,满足勾股定理,所以 1BC BC ,由线面垂直的判定定理证明 1C B  平面 ABC ；（2）先求出三棱锥 1 1A B BC 的 体积,利用等体积法求出点 B 到平面 1 1ABC 的距离． 试题解析：（1）因为 1 1AB BB C C ， 1BC  侧面 1 1BBC C ，故 1AB BC ， 在△ 1BCC 中， 1BC  ， 1 1 2CC BB  ， 1 60BCC   ， 由余弦定理得： 2 2 2 1 1 1 12 cosBC BC CC BC CC BCC     2 21 2 2 1 2 cos 33        ， ∴ 1 3BC  ，故 2 2 2 1 1BC BC CC  ，所以 1BC BC ， 而 BC AB BI ， ∴ 1C B  平面 ABC ． （2）∵ 1 1 1 1 1 1 1 3 3 2 6A B BCV BC B C AB       ， 又 2 2 1 1 5AB AB BB   ， 2 2 1 1 2AC AB BC   ， 1 1 1B C  ， ∴ 1 1 1 1 1 12AB CS AC BC    ， 设点 B 到平面 1 1ABC 的距离为 h ， ∴ 1 1 1 1 1 1 313 3 6B AB C AB CV S h h       ， ∴ 3 2h  ，∴点 B 到平面 1 1ABC 的距离为 3 2 ． 考点：1.线面垂直的判定定理；2.等体积法求点到面的距离. 19.某城市100户居民的月平均用电量（单位：度），以 160,180 ， 180,200 ， 200,220 ，  220,240 ， 240,260 ， 260,280 ， 280,300 分组的频率分布直方图如图． - 17 - （1）求直方图中 的值； （2）求月平均用电量的众数和中位数； （3）在月平均用电量为 220,240 ， 240,260 ， 260,280 ， 280,300 的四组用户中， 用分层抽样的方法抽取 户居民，则月平均用电量在 220,240 的用户中应抽取多少户？ 【答案】（1） 0.0075；（2） 230 ， 224 ；（3） 5 ． 【解析】 【详解】试题分析：（1）由直方图的性质可得（0.002+0.0095+0.011+0.0125+x+0.005+0.0025） ×20=1，解方程可得；（2）由直方图中众数为最高矩形上端的中点可得，可得中位数在[220， 240）内，设中位数为 a，解方程（0.002+0.0095+0.011）×20+0.0125×（a-220）=0.5 可得； （3）可得各段的用户分别为 25，15，10，5，可得抽取比例，可得要抽取的户数 试题解析：(1)由直方图的性质可得(0.002＋0.0095＋0.011＋0.0125＋x＋0.005＋ 0.0025)×20＝1 得： x＝0.0075，所以直方图中 x 的值是 0.0075. ------------- 3 分 (2)月平均用电量的众数是 220 240 2  ＝230. ------------- 5 分 因为(0.002＋0.0095＋0.011)×20＝0.45<0.5，所以月平均用电量的中位数在[220,240)内， 设中位数为 a， 由(0.002＋0.0095＋0.011)×20＋0.0125×(a－220)＝0.5 得：a＝224，所以月平均用电量的中位数是 224. ------------ 8 分 (3)月平均用电量为[220,240)的用户有 0.0125×20×100＝25 户， 月平均用电量为[240,260)的用户有 0.0075×20×100＝15 户， 月平均用电量为[260,280)的用户有 0. 005×20×100＝10 户， 月平均用电量为[280,300]的用户有 0.0025×20×100＝5 户， -------------10 分 - 18 - 抽取比例＝ 11 25 15 10 5   ＝ 1 5 ，所以月平均用电量在[220,240)的用户中应抽取 25× 1 5 ＝5 户．-- 12 分 考点：频率分布直方图及分层抽样 20.在平面直角坐标系 xOy 中，椭圆C ： 2 2 2 2 1( 0)x y a ba b     的离心率为 1 2 ，右焦点 (1,0)F . （1）求椭圆C 的方程； （2）点 P 在椭圆C 上，且在第一象限内，直线 PQ 与圆 O ： 2 2 2x y b  相切于点 M ，且 OP OQ ，求点Q 的纵坐标 t 的值． 【答案】（1） 2 2 14 3 x y  ；（2） 2 3t   . 【解析】 试题分析：（1）由 2 2 21 , 1,2 ce c a b ca      求出 , ,a b c 的值；（2）先考虑特殊情况:直线 PM 的斜率不存在,求出 2 3t  ；一般情况,直线 PQ : 0 0( )y y k x x   ,利用直线与圆相切,向 量垂直的条件:数量积为零,求出点Q 的纵坐标 t 的值． 试题解析：（1） 1 ,{ 2 1, c a c   ∴ 1c  ， 2a  ，∴ 3b  ，∴椭圆方程为 2 2 14 3 x y  ． （2）①当 PM x 轴时， 3( 3, )2P ， ( 3, )Q t ， 由 0OP OQ   ，解得 2 3t  ． - 19 - ②当 PM 不垂直于 x 轴时，设 0 0( , )P x y ， PQ 方程为 0 0( )y y k x x   ，即 0 0 0kx y kx y    ， ∵ PQ 与圆O 相切，∴ tan( )2 r R   ， ∴ 2 2 0 0( ) 3 3kx y k   ， ∴ 2 2 2 2 0 0 0 02 3 3kx y k x y k    ， 又Q 0 0( , )t y kx tk   ，所以由 0OP OQ   ，得 0 0 0 0 0 ( )x y kxt x ky   ， ∴ 2 2 2 0 0 2 0 0 ( ) ( ) x y kxt x ky   2 2 0 0 0 2 2 2 0 0 0 0 ( ) 2 x kx y x k y kx y    2 2 0 2 2 2 2 2 2 2 0 0 0 0 (3 3) 3 3 x k x k y k x y k       2 2 0 2 2 2 2 2 0 0 (3 3) 123(1 ) (1 )(3 ) 3 34 x k k x k x k         ， ∴ 2 3t   ． 综上： 2 3t   ． 考点：1.椭圆的简单几何性质；2.向量垂直条件. 【思路点晴】本题主要考查直线,圆椭圆之间的位置关系,属于中档题. 在（1）中,利用椭圆 的离心率和焦点坐标,求出椭圆的标准方程；在（2）中,分两种情况讨论,直线 PQ 的斜率是否 存在,分别求出点Q 的纵坐标 t 的值,要用到直线和圆相切的条件: d r ,直线垂直得到向量 垂直,向量数量积为零,再化简整理,求出 t 的值. 21.已知函数 2( ) ( 1) (1 ln )   f x x mx x （1）当 2m  时，求 ( )y f x 在 1 ex  处的切线方程； （2）若函数 ( )f x 有极大值点 0 0( 1)x x  ，求证 0( ) 1f x  . 【答案】（1） 2 2 1 2 e e ey x   +1；（2）证明见解析. 【解析】 【分析】 （1）根据导数的几何意义求出斜率，即可求出切线方程； - 20 - （2）利用 f' (1) =0,分析当 m≤0 时,函数 f (x) 无极大值点，得出矛盾，当 m>0 时，函数 f (x)有极大值点，分析函数 f (x) 的单调性得出 m 的取值范围,利用  0 0f x  得出 m 与 0x 所 满足的关系式，并得出 0x ∈(0， 1) ，并将关系式代入 f ( 0x ) 的代数式，将所证不等式转 化为以 0x 为唯一变量的不等式，利用导数证明即可. 【详解】 ( )f x 的定义域为 (0, ) ，   2 2f x x mlnx    ， (1) 2m  时， 1 2 1 2( ) 2 2e e e ef ln     ， 2 2 1 1 2 1 1 2( ) ( 1) (1 )e e e e e ef ln      +1， 曲线 ( )f x 在 1 ex  处的切线方程为 2 1 2 2 1( ) ( )e e e ey x   +1 即 2 2 1 2 e e ey x   +1 (2)  1 0f   ，   2 mf x x    ①当 0m  时，   0,f x   f x 是 (0, ) 上的增函数，  f x 只有 1 一个零点，不合题意， ② 0m  时，由   0f x  得 2 mx  ， 由   0f x  得 ( )f x 的增区间 ( , )2 m  ；由   0f x  得 ( )f x 的减区间 (0, )2 m ， ( )f x 最小值为 ( )2 mf  1 当 12 m  时， 即 2m  ， ( ) (1) 0f x f   ， ( )f x 在 (0, ) 上为增函数，不合题意； 2 当 12 m  时，即 2m  时， (0,1)x 时， ( ) (1) 0, (1, )2 mf x f x    ， ( ) (1) 0f x f   , 1 是唯一极大值点，不合题意； 3 当 12 m  ，即 0 2m  时， (1, )x  时， ( ) (1) 0,f x f   ( ,1)2 mx 时， ( ) (1) 0f x f   ， ( ) 02 mf   ； 2 2 2 2 (e ) 2e lne 2 2e 0m m m mf m          Q - 21 - 0 (0, )2 mx  ，使 0( ) 0f x  ，当 0(0, )x x 时， ( ) 0f x  ， 0( ,1)x x 时， ( ) 0f x  ， 0x 为 ( )f x 的极大值点，且 0 01x （ ，） 由 0 0 0( ) 2 ln 2 0f x x m x    ，得 0 0 2 2 ln xm x  ， 2 2 20 0 0 0 0 0 0 0 0 0 2 2 2 2( ) 1 + (1 ln ) 1ln ln x x xf x x x x xx x         （ ） 要证 0( ) 1f x  ，即证 2 2 0 0 0 0 2 2 1 1,ln x xx x     0 0ln x Q ， 需证 0 0 0ln 2 2 0x x x   ， 令 ( ) ln 2 2, (0,1)g x x x x x    ， 则 ( ) ln 1 2 ln 1 0g x x x      ， ( )g x 在 (0,1) 上为减函数 ， 故 ( ) (1) 0g x g  ， 0 0 0ln 2 2 0x x x    成立， 即 0( ) 1f x  . 【点睛】本题考查利用导数研究函数的极值,考查极值点的定义，考查推理能力与分析能力， 属于难题. 请考生在第 22、23 题中任选一题作答，如果多做，则按所做第一题计分.作答时请写清题号. 选修 4-4：坐标系与参数方程 22. 选修 4-4：坐标系与参数方程 在极坐标中，已知圆C 的圆心 (3, )6C  ，半径 3r  ． （1）求圆C 的极坐标方程； （2）若点Q 在圆 C 上运动，点 P 在OQ 的延长线上，且 : 3:2OQ OP  ，求动点 P 的轨迹 方程． - 22 - 【答案】（1） =6cos 6      ；（2） =10cos 6      ． 【解析】 【分析】 （1）设 ( , )M   为圆 C 上任一点， OM 的中点为 N ， ,6MOC CN OM    ,所以 cos( ) 3cos( ),| | 2 | | 6cos( )6 6 6ON OC OM ON           ,为所求； （2）先由 : 3:2OQ OP  求出点Q 的坐标,再由点Q 在圆上，所以 3 6cos( )5 6    ，化 简就可得到动点 P 的轨迹方程． 【详解】（1）设 ( , )M   为圆 C 上任一点，OM 的中点为 N ， ∵O 在圆C 上，∴△OCM 为等腰三角形，由垂径定理可得 cos( ), 6cos( )6 6ON OC        ，为所求圆C 的极坐标方程． （2）设点 P 的极坐标为 ( , )  ，因为 P 在 OQ 的延长线上，且 : 3:2OQ OP  ， 所以点Q 的坐标为 3( , )5   ， 由于点Q 在圆上，所以 3 6cos( )5 6    ， 故点 P 的轨迹方程为 10cos( )6    ． 考点：简单曲线的极坐标方程. 选修 4-5：不等式选讲 23.已知函数   2 1 ,f x x x R   ， （1）解不等式   1f x x  （2）若对于 ,x y R ，有 1 11 , 2 13 6x y y     ，求证：   1f x  . 【答案】（1）(0，2)；（2）证明见解析 【解析】 【分析】 （1）由条件把要解的解绝对值不等式等价转化为﹣x﹣1＜2x﹣1＜x+1，从而求得 x 的范围． （2）由条件利用绝对值三角不等式证得不等式成立． 【详解】解：（1）不等式 f(x)＜x+1，等价于|2x﹣1|＜x+1，即﹣x﹣1＜2x﹣1＜x+1， - 23 - 求得 0＜x＜2， 故不等式 f(x)＜x+1 的解集为(0，2)； （2） 1 11 , 2 13 6x y y     ， 所以 f(x)=|2x﹣1|=|2(x﹣y﹣1)+(2y+1)|≤|2(x﹣y﹣1)|+|(2y+1)|≤2 1 3  + 1 6 ＜1. 【点睛】本题主要考查绝对值不等式的解法，绝对值三角不等式的应用，体现了转化的数学 思想，属于基础题 - 24 -