- 85.00 KB
- 2021-02-26 发布
课题: 9.5 多项式的因式分解(4)
学习目标:
1.进一步熟悉提公因式法、平方差公式、完全平方公式分解因式;
2.能根据不同题目的特点选择较合理的分解因式的方法;
3.知道因式分解的方法步骤以及因式分解最终结果的要求.
教学方法:
学习过程:
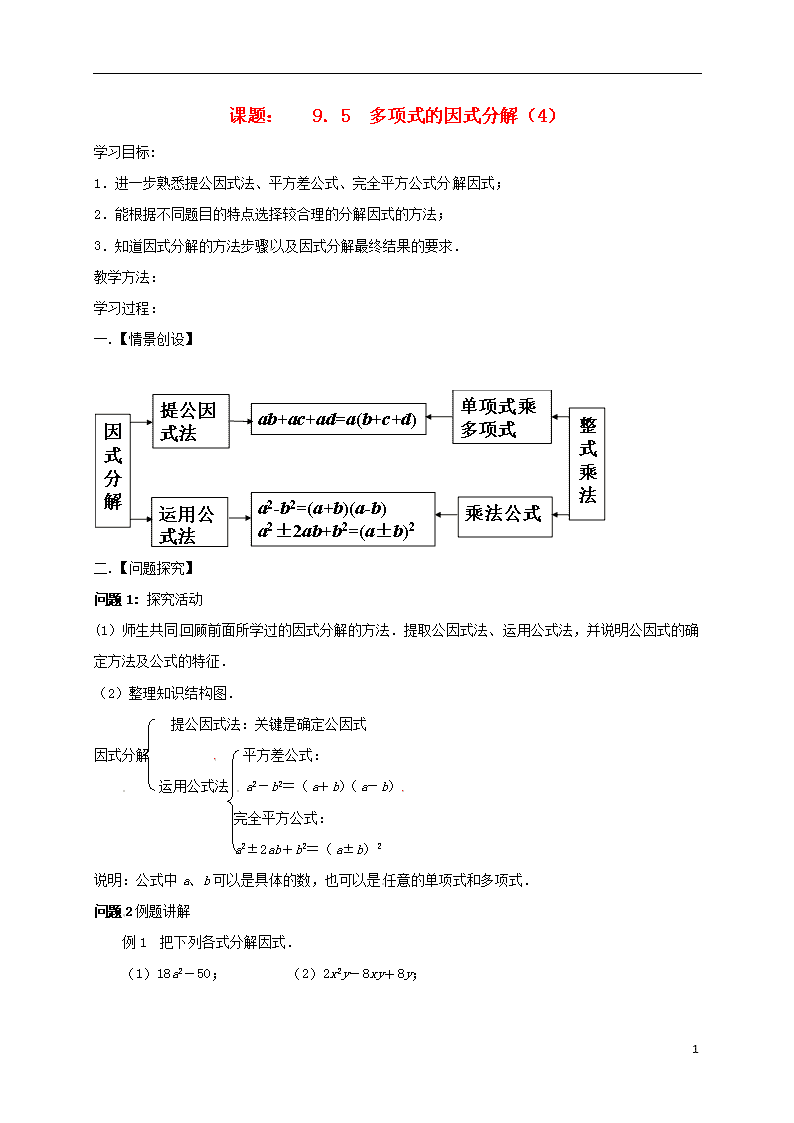
一.【情景创设】
二.【问题探究】
问题1: 探究活动
(1)师生共同回顾前面所学过的因式分解的方法.提取公因式法、运用公式法,并说明公因式的确定方法及公式的特征.
(2)整理知识结构图.
提公因式法:关键是确定公因式
因式分解 平方差公式:
运用公式法 a2-b2=(a+b)(a-b)
完全平方公式:
a2±2ab+b2=(a±b)2
说明:公式中a、b可以是具体的数,也可以是任意的单项式和多项式.
问题2例题讲解
例1 把下列各式分解因式.
(1)18a2-50; (2)2x2y-8xy+8y;
2
(3)a2(x-y)-b2(x-y).
问题3例2 把下列各式分解因式.
(1)a4-16; (2)81x4-72x2y2+16y4.
三【变式拓展】
问题4.把下列各式分解因式;
(1)(a2+b2)2-4a2b2 (2)(x2-2x)2+2(x2-2x)+1.
问题5利用因式分解计算:
(1) (2)44×29-11×34
四.【总结提升】
通过本节课的学习,你有哪些收获?
选做题
2